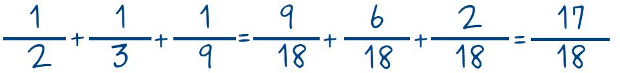–No se puede, Sal –dijo Ven.

–Espera, Ven, yo creo que sí –respondió el gafotas.

–Pero nunca serán igual de altas –insistió el pequeño — ¿No ves que los cubos de números son más pequeños que los cubos de letras?

–Que eso no impoooooorta… –contestó el gafotas.

–¡Anda que no! –siguió Ven con la regla en la mano –¡Mira! Los de letras miden 9 centímetros y los de números solo miden 6 centímetros de lado.

–Pero, bueno… –Mati acababa de llegar –¿Qué pasa aquí? Cuánto jaleo…

–Hola, Mati –la saludó Sal –. Vamos a construir dos torres gemelas con los cubos, una de letras y otra de números, para demostrar que las mates son tan importantes como las letras –el gafotas guiñó un ojo.

–Pero es imposible, porque los cubos de letras son más grandes que los de números –añadió su hermano con retintín.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

–Hola, Ven –saludó la pelirroja –No, ¿por qué dices que es imposible?

–Porque los de letras miden 9 centímetros y los de número 6 –contestó el pequeño cada vez más enfadado.

–Vamos a pensar un poco –propuso ella –Si hacemos una torre con 8 cubos de letras, ¿cuánto medirá?

–72 centímetros… –dijo Ven con cansancio.

–Eso es, Ven –dijo Mati –9 por 8, es decir, un múltiplo de 9, ¿no?

–Pues claro –contestó Ven mirando a Mati por el rabillo del ojo.

–Y si hacemos una torre con 10 cubos de números, ¿cuánto medirá? –siguió preguntando ella.

–60… –respondió Ven.

–Ajá, un múltiplo de 6, ¿no? –les preguntó.

–Sí  –respondió el gafotas con interés.

–Luego el problema que tenemos que resolver es encontrar un número que sea, a la vez,  múltiplo de 9 y múltiplo de 6 –les dijo –. Un múltiplo común a 9 y 6.

–Ya lo tengo –gritó el gafotas –Basta poner 6 cubos de letras y 9 cubos de números, y medirán 54 centímetros las dos torres ¡Guay!

–Muy bien, Sal –dijo Mati mientras Ven dudaba entre enfurruñarse por haber perdido la disputa y alegrarse porque el problema tenía solución –Ahora os pregunto, ¿se pueden hacer dos torres gemelas más pequeñas que esas con cubos de 6 y 9 centímetros de lado?

Los niños se quedaron muy serios, Gauss ladró para disimular y empezó a perseguir a una mosca imaginaria. Él es así.

–Ni i-d-e-a –acabó admitiendo Ven.

–Se trataría de encontrar el menor múltiplo que tienen en común 6 y 9, ¿no? –dijo Mati –Lo que se suele llamar mínimo común múltiplo de 6 y 9, y que se escribe así: mcm (6,9).

–¿Y eso cómo se hace, Mati? –preguntó enseguida Sal impaciente.

–Hay otras formas de hacerlo –les contó –, pero a mí me resulta más fácil calcularlo usando el máximo común divisor, ¿os acordáis?

–Sí, sí –dijo Sal –. Nos lo contaste. Se hacía con el algoritmo de Euclides, ¿no?

–Efectivamente, cielo –dijo Mati –Pues bien, el mínimo común múltiplo de 2 números se puede calcular dividiendo el producto de esos dos números entre el máximo común divisor de estos.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

–Vamos a calcular el mcm(6,9) –les propuso –.Para ello vamos a calcular primero MCD(6,9) usando el algoritmo de Euclides.

–¡Vale! –dijeron los dos hermanos a la vez.

 

 

 

 

 

 

 

 

 

–Ea, pues ya lo tenemos –les dijo la gafotas.

 

 

 

 

–¡Claaaaaro! –exclamó Sal –Basta con poner 2 cubos de letras y 3 de números, ¡era muy fácil!

–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven.

–¿Veis? Era posible –dijo Mati guiñando un ojo –Os voy a proponer ahora aun acertijo. Imaginaos que vuestros padres os dan paga cada semana, cada 7 días; vuestros abuelos os dan paga cada 14 días y yo os doy una paga cada 35 días…

–Ojalá –dijo Ven con una sonrisa pícara.

—Si os damos las 3 pagas hoy por primera vez –les dijo —¿cuándo volveremos a daros los 3 la paga a la vez?

Los niños se quedaron pensando muy serios,  hasta que Sal dijo:

–¿Hay que calcular el mínimo común múltiplo de 7, 14 y 35?

–¡Muy bien! –dijo Mati.

–¿Y cómo calculamos el mínimo común múltiplo de 3 números? –preguntó Ven.

–Pues agrupando, convenientemente, por parejas –respondió Mati –, así:

 

 

 

 

 

 

 

 

–Calculamos primero mcm(7,14) –les dijo.

 

 

 

 

 

–Nos sale 14 –continuó la pelirroja –. Ahora tendríamos que calcular mcm(14, 35) 

 

 

 

 

 

–¡Es 70! –dijo Sal de pronto.

–Así que no volverán a coincidir las 3 pagas hasta dentro de 70 días –concluyó Mati.

–¡Hala, qué morro! –se quejó el pequeño.

–Pero si era todo ficticio, Ven… –se burló el gafotas.

–Con este método para calcular el mínimo común múltiplo –les contó Mati —evitamos tener que factorizar en primos, que puede ser muy complicado. Pensad, por ejemplo, que si queremos descomponer en factores primos el número 7663, el primer factor primo que  tiene es 79, y para llegar hasta él hemos tenido que probar con muchos primos antes…

–Jo, pues sí que es difícil factorizar… –se quejó Ven.

–Venga, el último acertijo –les dijo Mati —Ahora tenemos 25 bolitas rojas, 15 bolitas azules y 45 bolitas verdes. Queremos hacer collares exactamente iguales sin que sobren bolitas, ¿cuántos collares como máximo puedo hacer?

Los niños se volvieron  aquedar muy serios. Finalmente Ven preguntó:

–¿Hay que hacer el mcm(25, 15, 45)?

–No, no –dijo Mati –Si queremos que todos los collares sean iguales, todos tienen que tener el mismo número de bolitas rojas, ¿no?

Los niños asintieron con la cabeza. Gauss también.

–Por lo tanto –siguió la pelirroja –,  tenemos que dividir el número de bolas rojas entre el número de collares y, si no queremos que sobren bolas rojas, el número de collares debe ser un divisor del número de bolas rojas, de 25, ¿verdad?

Sal y Ven volvieron a asentir. Gauss también, es muy novelero.

–Lo mismo ocurre con las bolas azules –continuó ella –por lo que el número de collares debe ser divisor de 15.

–Y también divisor de 45… –apostilló Sal –por las bolitas verdes.

–Eso es –dijo Mati –El número de collares debe ser un divisor común de 25, 15 y 45, y como queremos hacer el mayor número de colares posibles, será el MCD(25, 15, 45). Hacemos primero el MCD(45, 25)

 

 

 

 

 

 

 

 

 

–Y por último, el MCD(15,5)

 

 

 

 

 

 

 

 

 

 

–Ya tenéis, les dijo que el MCD(25, 15, 45) es 5 –continuó Mati –Así que podréis hacer como máximo 5 collares iguales.

–¡Claro! –exclamó Sal –Cada collar tendrá 5 bolitas rojas, 3 bolitas azules y 9 bolitas verdes.

–¡Qué chulo, Mati! –dijo Ven.

–¿Os gusta? –preguntó ella sonriendo –Pues el próximo día os enseñaré a sumar fracciones usando lo que aprendimos hoy.

–¡¡Guauuu!! –dijo Gauss que siempre tiene que ser el que diga la última palabra…