–Descansa un poco, Sal. Ya te sale muy bien…
–No, no estoy seguro, Ven. Quiero hacerlo muy bien en la función del Día de Andalucía.
–¿Vais a tocar todos los de tu clase a la vez? –preguntó Ven.
–Claro –respondió el gafotas –¿Por qué?
–En ese caso te recomiendo que no soples demasiado… –le sugirió el pequeño.
–¿¿Por qué?? –preguntó Sal extrañado.
–No sé, no te sale muy bien –respondió el pequeño mirando a otro lado.
–Acabas de decir lo contrario, Ven –respondió Sal –. Mentiroso… Voy a seguir ensayando.
–No, de verdad –suplicó Ven –. Nos estás martirizando…
–Se trata de celebrar el día de nuestra comunidad autónoma, Ven –le espetó Sal con aire digno –. Me parece que no eres consciente de la importancia de esta función…
–Huy, todas las funciones son muy importantes –Mati acababa de llegar –, al menos, a los matemáticos nos apasionan.
–Hola, Mati –la saludó el pequeño Ven muy contento — ¿Nos vamos al parque con Gauss?
La mascota comenzó a mover la cola con entusiasmo ante la propuesta de Ven.
–Hola, Mati –la saludó Sal serio — ¿Por qué te gustan tanto las funciones? ¿Las de música?
–Esas también –respondió la pelirroja –, pero me refería a las funciones matemáticas.
–¿Qué son funciones matemáticas? –preguntó el pequeño y añadió con cara de pillo –¿Cantáis sumas y multiplicaciones?
–No, no es eso –le contestó ella con un guiño –Una función matemática no es más que una regla o ley que te permite asignar a cada elemento de un primer conjunto un único elemento de otro conjunto.
–No entiendo… –aceptó Ven.
–Os lo explico con un ejemplo –propuso ella –. Una función podría ser asignar a cada número el valor de su cuadrado. Al 1 le asignamos el 1, al 2 le asignamos el 4, al 3 le asignamos 9… y así sucesivamente.
–¡Eh, un momento! –dijo Ven –Has asignado el mismo número al 1 y al -1. Eso no vale.
–Sí, Ven, sí vale –dijo Mati –. A dos elementos del primer conjunto se les puede asignar el mismo elemento del segundo conjunto. Piensa por ejemplo en una función que a cada palabra del castellano le asignara su primera letra. Habría muchas palabras que tendrían asignada la a, por ejemplo.
–Toma, claro –aceptó el pequeño.
–Pero en matemáticas estudiamos, principalmente, funciones entre conjuntos numéricos –continuó la pelirroja –. A las funciones se les suele llamar f, de función, y la función que hemos descrito que asigna a cada número su cuadrado se escribiría así:
–Eso significa –continuó Mati –que f transforma lo que está entre paréntesis, x, en eso mismo, x, al cuadrado. Nuestro amigo Fis dice que le parece una f embarazada, con su x en la tripa.
–¡Toma! ¡Es verdad! –dijo Ven divertido.
–Pues sí, no lo había pensado nunca, pero sí –añadió Mati –. Yo siempre las veo como una especie de máquina, en las que entra un número y sale transformado.
–¿Para qué sirven las funciones, Mati? –preguntó Sal.
–Huy, para muchísimas cosas –respondió Mati –. Por ejemplo, se pueden usar para estudiar fenómenos físicos, químicos, económicos…
–¿Nos dices otra función Mati? –pidió el pequeño.
–Pues sí, de hecho ya os he dicho algunas anteriormente –respondió ella –, aunque no la llamásemos así. Pero cuando estudiábamos las ecuaciones de las rectas, estábamos dibujando funciones.
–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven.
–No entiendo, Mati –resopló el gafotas.
–Intentaré explicarlo –anunció ella –. Hay varias formas de representar una función. Una, ya la hemos visto, escribiendo f(x)=x2 . A x se le llama variable independiente de la función y, como veis, representar de esta forma una función consiste, simplemente, en escribir una expresión en la que aparece la variable, x, por ejemplo: f(x)= x2, f(x)= 3x3-1, f(x)=x/2…
–Ajá –dijo Ven muy serio, Sal miró a su hermano por encima de sus gafotas.
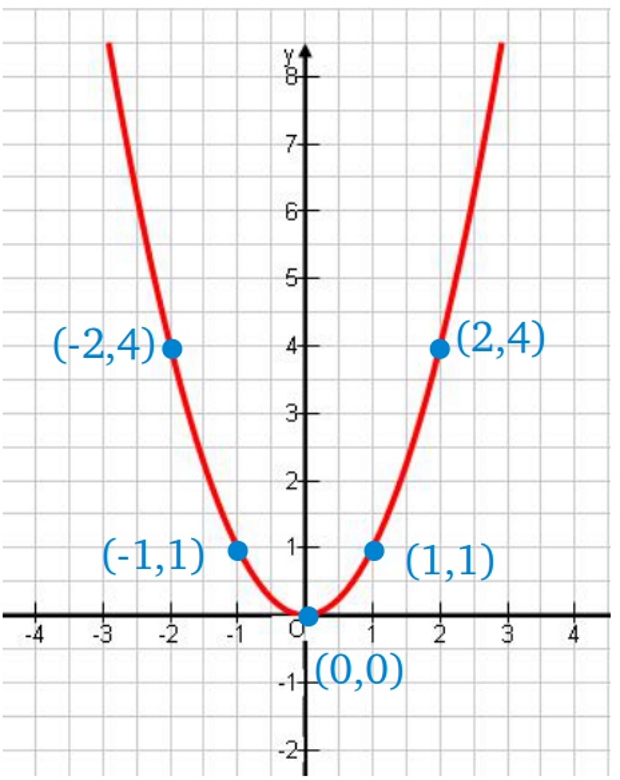
–Pues bien –continuó ella –, cada función de x se puede representar también como una curva en el plano. Para ello, vamos a dar algunos valores, los que queramos, a la variable x y pintamos en el plano cartesiano, los puntos de coordenadas (x, f(x)), como aprendimos cuando estudiamos las coordenadas cartesianas.
–A mí me gustan más las coordenadas polares… –interrumpió el pequeño, Sal le recriminó con la mirada y Mati siguió:
–Vamos a escribir, para ayudarnos, una tabla donde ponemos los valores que le vamos dando a x y el correspondiente valor que le asigna f(x)= x2
–Esto significa –prosiguió ella –que la gráfica de nuestra función, f(x)= x2, pasa por los puntos de coordenadas: (-2,4), (-1, 1), (0,0), (1,1) y (2,4). Pues bien, la gráfica de nuestra función f(x)= x2 es la siguiente curva roja, llamada parábola.
–¡Mola! –dijo Ven.
–Ahora, si tenemos la ecuación de una recta, por ejemplo , en forma implícita –continuó la pelirroja –, 2x-3y+1=0, vamos a dejar solita a la y en la izquierda de la expresión y pasamos el resto de términos a la derecha.
–¿Veis? –preguntó Mati.
–¿¿Qué?? –dijeron los dos hermanos a la vez.
–Tenemos que y es igual a una expresión de x –respondió ella –. Cuando esto ocurre, decimos que y es una variable dependiente de x y tenemos, por lo tanto, una función de x:
–¿Cómo sabes que eso es una función de x? –preguntó el gafotas.
–Porque es una máquina que transforma números en otros –respondió ella guiñando un ojo.
–¡Moooooooooooooola! –volvió a exclamar el pequeño.
–Sí, mola –corroboró Mati –. La recta de ecuación 2x -3y +1=0 es la gráfica de la función f(x)=(2x+1)/3.
–¿Todas las rectas son gráficas de una función, Mati? –preguntó el gafotas.
–Todas, menos las rectas verticales –dijo ella –. Basta que despejéis, en la ecuación de la recta, el valor de y y lo que os salga es la función de x que estáis representando.
–¡Toma! –exclamó Ven –¡Y lo podremos hacer también con las ecuaciones de las circunferencias!
–¡No! –dijo de pronto Mati –Las circunferencias no son la gráfica de una función, sino de 2 funciones…
–Sí, hombre… –dijo Ven desconfiado.
–Piensa un poco –le retó la pelirroja –, a ver si sabes por qué. Pero ahora vamos que es la hora de la función de Sal.