En capítulos anteriores vimos cómo la distancia más corta entre dos puntos de la superficie terrestre no siempre es lo que parece. Así, la distancia más corta entre Sevilla y la capital de las Islas Salomón viene dada por esta curva:

Pero, ¿es ese un fenómeno que se da sólo porque la esfera no es plana? ¿si nos restringimos a porciones más pequeñas de la Tierra, como ciudades, que son casi un plano, podemos considerar que la línea recta es la distancia más corta entre dos puntos? Bueno, la verdad es que no del todo puesto que otras consideraciones aparecen en este caso. Así que tratemos de fijar conceptos:
Supongamos que estamos en una gran ciudad y queremos llegar de un punto a otro, ¿consideraremos la recta como el camino óptimo? Si se puede ir en línea recta sí, pero, en general la línea recta entre dos puntos en una ciudad implica atravesar edificios lo cual puede traer inconvenientes que no ha lugar considerarlos aquí. Entonces me parece que no es mala idea buscar la distancia más cortas en una ciudad «andando por las calles» (el problema de circular es ligeramente más complicado puesto que implica direcciones únicas). como paradigma de ciudad para este ejemplo se suele tomar es el de la parte central de Manhattan por estar muy bien estructurado.Así supongamos que queremos ir de un punto a otro de Manhattan (con o sin la compañía de Euclides) y que no vamos a atravesar rascacielos porque eso no está bonito, no. ¿Cuál será esa ruta?
 |
| Figura 1 |
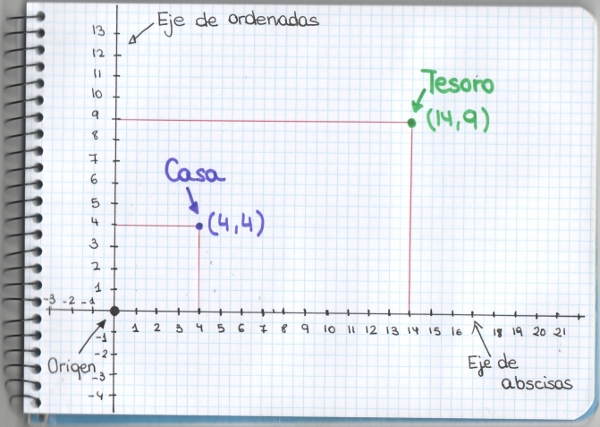
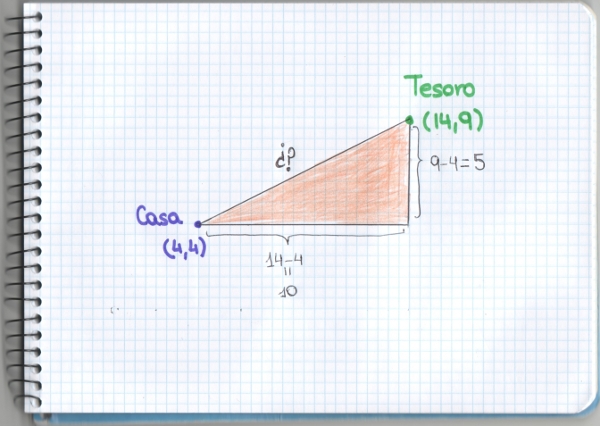
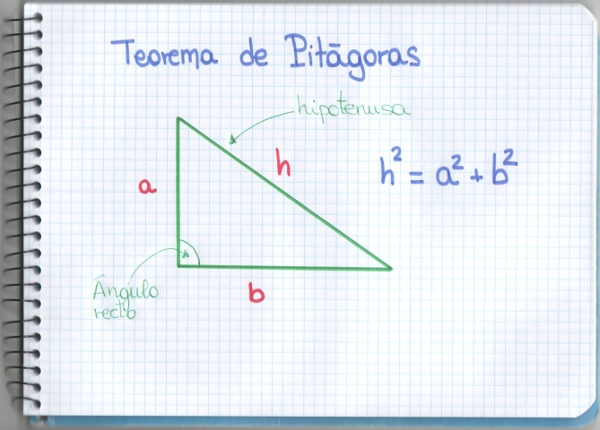
En la Geometría Euclideana, que es la geometría que todos aprendemos desde nuestros primeros años de estudios, la distancia entre dos puntos se mide como la longitud del segmento que los une, o dicho de otra forma, como el módulo del vector que esos dos puntos definen. Esa forma de medir la distancia es conocida como distancia euclídea y es la que usamos cuando medimos usando un metro entre los dos extremos de lo que queremos medir. En realidad, se trata de una consecuencia del Teorema de Pitágoras. Si tenemos dos puntos en el plano de coordenadas (a,b) y (c,d) respectivamente y queremos calcular la distancia euclídea entre ellos, basta con fijarse que la longitud de los catetos del triángulo rectángulo que definen son (c-a) la de uno y (d-b) la del otro. Entonces, por el Teorema de Pitágoras, sabemos que la distancia euclídea se mide como
Ahí todo está bien y correcto, pero esa no es la única forma de medir la distancia entre dos puntos en el plano. Existe otra distancia, conocida como Distancia de Manhattan o Distancia L1, que mediría la distancia entre los puntos de la Figura 1 como
Es decir, la suma de las longitudes de los dos catetos del triángulo rectángulo. O bien, la de cualquier ruta que una al punto (a,b) con el punto (c,d) a través de segmentos horizontales y verticales, en otras palabras, la longitud de cualquier escalera que suba desde (a,b) con el punto (c,d)
 |
| En verde, la distancia euclídea, y en rojo, azul y amarillo, la distancia Manhattan: todas ellas son rutas óptimas. (Imagen sacada de aquí) |
Pues bien, cuando se trata de diseñar rutas de recorrido mínimos en ciudades, tiene más sentido usar esta distancia que la Euclídea, por lo de no atravesar rascacielos que habíamos dicho. Es más, puesto que todas las ‘escaleras’ tienen la misma longitud, nos permite elegir entre distintas opciones, en función de semáforos, zonas de dudosas seguridad, etc…
Evidentemente, no todas las ciudades, ni siquiera Nueva York, están distribuidas como una cuadrícula, pero se considera para según qué problemas de dieños de rutas este tipo de distancia. Y también, cómo no, en el diseño de circuitos ortogonales en los que predominan la conexiones en vertical y horizontal, o en el de un plano de metro.
Otra cosa que no diríamos si pensáramos con la distancia de Manhattan es “No había nadie en 10 Km a la redonda” Porque cuando utilizamos esta expresión, estamos intrínsecamente midiendo con la distancia euclídea. Con esta distancia, la que usamos habitualmente en el día a día, los puntos que están a menos distancia de 10 Km de nosotros, son aquellos que están contenidos en un círculo alrededor nuestra de radio 10 Km.
Pero si pensáramos con la distancia de Manhattan, no sería un círculo, sino ¡un rombo!
Todos los puntos de la frontera del círculo de la izquierda están a la misma distancia euclídea del origen de coordenadas, y todos los puntos de la frontera del rombo de la izquierda están a la misma distancia L1 del origen de coordenas, como se explica en la siguiente figura:
Ahora vamos a ver, que dependiendo de la distancia elegida, el punto más cercano a uno dado puede ser distinto, lo que sería de utilidad conocer a la hora de diseñar rutas de longitud mínima, por ejemplo, para empresas de distribución, mensajería…
 |
|
Si usamos la euclídea (la usual) el punto rojo está más cerca del origen (en azul) mientras que si usamos la de Manhattan el origen esá más cerca del punto verde. |
Eso sí, puede que la distancia Manhattan sea más práctica y refleje mejor la realidad en el diseño y optimización de rutas de distribución, pero mi experiencia como madre me permite asegurar que cuando somos niños es la distancia eulcídea la que ‘traemos’ instalada: «De aquí para acá, mío, de aquí para allá, tuyo».
Pues bien, ahora que ya conocemos la distancia Manhattan, os formulo una pregunta. Si tenemos dos puntos sobre el plano, P y Q, los puntos que están a la mitad de camino entre P y Q, a la misma distancia de ambos, definen una recta que conocemos, como mediatriz. ¿Y si usamos la distancia L1,? ¿Qué aspecto tiene la mediatriz entre P y Q?
PS: Cuando explico esta distancia a mis estudiantes no puedo resistir la tentación de llamarla Distancia del Ensanche, y es que Barcelona es mi debilidad (aunque Nueva York no está nada, pero nada mal).