Todos hemos visto alguna vez esas listas que aparecen en internet de gente experta en algún tema que nos dan consejos sobre prácticas convenientes o no en alguna red social o en algún apartado específico de la red. Normalmente, además, son consejos negativos: de cosas que no debemos hacer. En muchos casos, dichos consejos están dictados por el sentido común, en otros después de observar ciertas prácticas abusivas por parte de algunos usuarios y muchas son simplemente un corta y pega de otros consejos elaborados por otros. Son comunes las listas de prácticas de buena costumbre en Twitter, en Instagram o en Facebook. La verdad es que yo hubiera agradecido que algunos comentaristas de blogs se hubieran leído alguna lista de consejos sobre comentarios y la aplicaran. Así que me voy a animar y voy a dar una de dichas listas, casi se podría considerar una metalista, puesto que voy a dar consejos para elaborar cualquiera de esas listas de consejos:
Allá va mi lista:
10 consejos que has de seguir cuando quieras elaborar una lista de consejos sobre cualquier tema en internet:
- No dé consejos.
- …
Creo que he terminado mi lista un poco antes de lo previsto, pero ahora voy a tratar de justificarla y mi justificación, aunque parezca imposible, viene de la mano de algunos resultados matemáticos. Me explico:
Existen algunos problemas de optimización (encontrar el mejor valor que puede alcanzar una función) que no pueden resolverse por métodos clásicos y que, si tratamos de resolverlos con un ordenador, nos encontramos con un problema bastante serio como se verá. Para que se me entienda voy a escoger el más típico de dichos problemas de optimización. Ya hablamos de él en algún momento: el problema del viajante (TSP): en dicho problema, expresado de forma simple,se trata de visitar un conjunto de ciudades volviendo al punto de partida (se conocen las distancias entre ellas) recorriendo la menor distancia posible. 
Por extraño que parezca, a pesar de lo simple de su planteamiento, si el número de ciudades no es muy bajo no existe ningún método que nos permita encontrar la ruta óptima. Uno puede pensar que probando todas las combinaciones de ciudades se podrá encontrar la mejor. Pero nos encontramos con la dificultad de que todas las combinaciones, en general, es un número ingente. Supongamos que tenemos que visitar 100 ciudades, todas las combinaciones es 100! y este es un número más grande de lo imaginable (el número de partículas elementales en el universo observable es mucho menor). Por lo tanto, hemos de renunciar a encontrar la ruta óptima y limitarnos a conseguir una ruta aceptablemente buena. Para conseguir dicha ruta aceptablemente buena, un procedimiento que se suele utilizar es el llamado de Algoritmos Genéticos ¿Cómo funcionan los algoritmos genéticos? Pues los algoritmos genéticos tratan de simular el proceso darwinista mediante el cual la naturaleza consigue especies que se adapten a su medio. Voy a intentar explicarlo con el ejemplo de las ciudades:
Para simplificar, supongamos que tenemos 6 ciudades a las que denominamos A, B, C, D, E y F. Tratamos de encontrar la permutación óptima de dichas letras que nos de la distancia mínima. Los elementos que componen nuestro algoritmo genético son los siguientes:
En primer lugar necesitamos una población inicial con el número de individuos que decidamos de antemano, para obtener dicha población inicial nos basta con encontrar aleatoriamente tantas permutaciones como nos sean necesarias. Así entre todas las permutaciones posibles escogemos por sorteo unas cuantas. Supongamos que, en nuestro caso, la población inicial es de 6 individuos y construimos dichos individuos aleatoriamente y obtenemos los siguientes seis: ABEFDC, ABCEFD, AEBCFD, ACDBEF, AEFCDB y ADCBFE (empezamos siempre en la A que es donde está el punto de partida y entendemos que, al final, hemos de volver a A) . Como estos individuos los hemos construidos aleatoriamente, puede que ninguno de ellos se acerque, ni de lejos, a la solución óptima, pero nos da igual, eso no es importante. Lo siguiente que necesitamos es una función que nos diga cómo de buenos son los elementos de nuestra población. En este caso la función puede ser la distancia que tenemos que recorrer si seguimos el orden de cada permutación; esto es: para ABEFDC (y para todas las demás permutaciones), medimos la distancia de A a B, le sumamos la distancia de B a E, de E a F, de F a D, de D a C y de C a A, para obtener la distancia total de ABEFDC.
Así, cada uno de los individuos de nuestra población tendrá asignado un número y, en nuestro caso, cuanto más pequeño sea dicho número, mejor, más corta será la distancia que tengamos que recorrer. Esta función es lo que se llama la aptitud de los individuos, por lo tanto, en nuestro ejemplo cuanto más pequeña sea la distancia asociada a una permutación, más apta será dicha permutación.
Ahora le asignamos papeletas a cada individuo para realizar un sorteo, cuanto más apto sea un individuo (menos distancia tengamos que recorrer), más papeletas le asignamos para el siguiente sorteo que consiste en un proceso de selección: vamos a realizar emparejamientos por puro sorteo (pero los mejores individuos tienen más papeletas) y vamos a construir 3 parejas mediante dicho sorteo (puede que un mismo individuo salga dos o más veces en dicho proceso de emparejamiento). Supongamos que una de dichas parejas sea la formada por los individuos ABCEFD y ACDBEF, ahora vamos a cruzar a dichos individuos, vamos a obtener sus hijos, para construir la siguiente generación.
Hay varios métodos para hacer esto, en algunos casos es más simple describir dicho proceso, en otros un poco más complicado. Propongamos uno: hacemos otro sorteo y escogemos un lugar entre 2 y 4: supongamos que sale 3: eso significa que al cruzar ABCEFD con ACDBEF, vamos a obtener dos hijos, el primero escogemos las tres primeras ciudades de ABCEFD: ABC y el resto de las ciudades las recorremos: después de C, en el orden en el que aparecen en ACDBEF: después de C está D, después estaría B, pero como por B ya hemos pasado, nos la saltamos y vamos a E y por último a F; por tanto, el primer hijo sería ABCDEF. Ahora hacemos lo mismo empezando por ACDBEF, así las tres primeras ciudades serían ACD, en ABCEFD, la siguiente ciudad después de D es A, que nos la saltamos, después B, después C que nos la saltamos porque ya la hemos visitado, después E y por último F. Por lo tanto, a partir de ABCEFD y ACDBEF hemos obtenido dos hijos: ABCDEF y ACDBEF (que, curiosamente, es igual que uno de sus padres, pero no nos preocupamos por ello).
Por lo tanto, como teníamos tres parejas y de cada pareja hemos obtenidos dos hijos, tenemos ahora seis individuos de nuevo. Esos individuos los hemos obtenido intercambiando la información genética de la población inicial. Pero ahora interviene un elemento esencial, sin él el método no funcionaría, sin él la naturaleza no habría obtenido los individuos que mejor se adaptan a su habitat: la mutación. Mutaciones ocurren pocas y la mayoría son regresivas: dan peores individuos, pero , muy de vez en cuando, producen individuos mejor adaptados y sin ella el proceso darwiniano no tendría sentido. Así lo que hacemos es, una vez obtenidos los hijos, realizamos un nuevo sorteo pero tal que la probabilidad de ser mutado sea muy pequeña (digamos 1 entre 1000), por lo tanto, de cada 1000 individuos mutamos aproximadamente a 1. Supongamos que uno de los hijos que hemos obtenido en el proceso anterior ABCDEF sale mutante ¿qué hacemos? realizar otro sorteo (ya llevamos unos cuantos) y sacamos dos números entre el 2 y el 6, por ejemplo 3 y 5, pues intercambiamos las ciudades que aparecen en tercer y quinto lugar para obtener ABEDCF.
Resumiendo:
a partir de la población inicial, escogemos parejas (por un sorteo asignando más papeletas a los mejores individuos), cruzamos dichas parejas (en un proceso en el que se intercambia la información de dichas parejas) y puede que mutemos algún individuo y con estas tres operaciones hemos construido la siguiente generación a la que le volvemos a aplicar el proceso y así tantas veces como se decida en un principio. Lo curioso es que hay un resultado matemático que nos asegura que, con este método, vamos a aproximarnos a la solución óptima tanto como queramos (cuantas más generaciones mejor) y que si algunos de los elementos no lo tenemos en cuenta puede que nunca nos aproximemos a dicha solución porque nos quedemos estancados en lo que se llama un óptimo local y nunca nos aproximemos al óptimo global que es lo que estamos buscando.
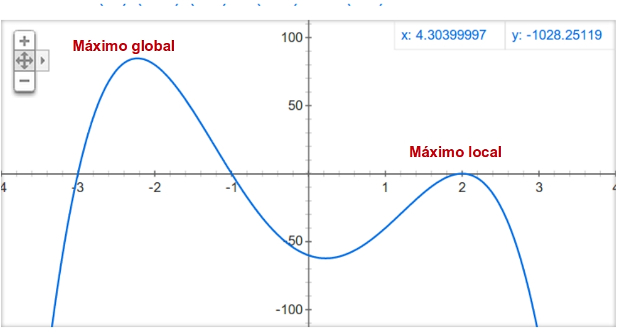
Y ¿qué tiene que ver todo esto con las listas de consejos en internet?
Pues que si seguimos las listas de consejos, no estamos siguiendo un proceso evolutivo: nos estamos estancando en óptimos locales ya que hacen que todos los individuos se parezcan y eliminamos diversidad que es fundamental para obtener mejores elementos. En algún sentido se puede decir que el mestizaje es fundamental para la mejora de la población (¿hacen alta más argumentos aún para probar lo estúpido del racismo?) y que poblaciones muy endógamas (como las familias reales), suelen degenerar y dar individuos muy defectuosos.
Mezclénse, por favor… Huy, al final he dado un consejo 😉