–¡Mira, Gauss! –exclamó Ven –¡Son Sheldon y Penny!
–¡Qué bien, Gauss! –añadió Sal –Hoy puedes jugar con tus amiguitos.
–Querrás decir con sus primos, ¿no, Sal?
–No, Ven. Sheldon y Penny no son primos de Gauss.
–¿Cómo que no son primos? Son las mascotas de nuestros tíos –protestó el pequeño –Entonces es como si fueran los primos de Gauss, ¿no lo entiendes?
–Que no, Ven –insistió el gafotas –Que los padres de Sheldon y Penny no son hermanos de los padres de Gauss…
–¿Y eso qué importa, Sal? ¡Son primos y punto! El tío es hermano de mamá así que…
–Lo que tú quieras, Ven. Pero eso no significa que sean primos entre ellos –siguió argumentando el mayor de los hermanos –Si no son de la misma raza siquiera…
–Vaya tontería lo de la raza –bufó Ven –¡Si vamos a tener una prima negra!
–Pero ella si es nuestra prima, porque es la hija de nuestra tía…
Gauss, Sheldon y Penny observaban a los niños con caras serias, no parecían entender aquella discusión sobre conceptos de familia…
–Pero bueno… –Mati acababa de despertarse de su siesta –¡Qué serios están estos chicos! ¿Algún desacuerdo sobre algún asunto matemático? –les dijo guiñando un ojo.
–No, Mati, un desacuerdo sobre primos o no primos –dijo el pequeño Ven mirando de reojo a Sal –No tiene nada que ver con Matemáticas.
–¿Cómo que no? –bromeó la pelirroja –Los números primos son uno de los objetos que más han fascinado a los matemáticos.
–Ya, Mati –intervino el gafotas –Pero no hablamos de números primos, sino de perros primos ¿Qué son números primos, Mati?
–Un número primo es aquel que sólo es divisible por sí mismo y por 1 –dijo la pelirroja –Por ejemplo el 2, el 3, el 5…
–¡Toma! –interrumpió Ven entusiasmado –¡Los números de la sucesión de Fibonacci!
–No, no son los números de la sucesión de Fibonacci –dijo Mati sonriendo –Porque ¿cuál viene detrás del 5 en esa sucesión, Ven?
–¿Después del 5? –Ven se quedó pensando –5 más el anterior que es el 3… ¡el 8!
–Efectivamente, Ven –continuó la pelirroja –Y 8 no es un número primo.
–Es verdad –dijo Sal –8 se puede dividir por 2 y por 4.
–Eso es, Sal. El 8 tiene a 2 y a 4 como divisores distintos de 1 y de él mismo, 8 –dijo ella –¿Qué os pasa con los perros primos?
–Que Sal dice que Gauss no es primo de Sheldon y Penny y yo digo que sí.
–Ah, entiendo –dijo Mati –Lo que queréis saber es si ellos son primos entre sí.
–Eso –corroboró el mayor.
–Con los números es mucho más fácil –continuó Mati –¿Queréis que os enseñe cómo saber si dos números son primos entre sí?
–¿Primos entre sí? –preguntó Sal ajustándose las gafotas –¿Qué significa que dos números son primos entre sí, Mati?
–Que no tienen ningún divisor en común, salvo el 1, claro –dijo ésta –Por ejemplo, 10 y 9 son primos entre sí.
–No, no lo son, Mati –dijo rápidamente Ven –9 se puede dividir por 3 y 10 se puede dividir por 2 y por 5.
–Sí, Ven –siguió la gafotas –Eso significa que 9 no es un número primo, porque tiene de divisor al 3; y que 10 no es un número primo porque tiene como divisores al 2 y al 5 –Mati continuó –Pero 9 y 10 son primos entre sí porque no tienen ningún divisor en común, sólo el 1 otra vez, claro.
–Ahora lo entiendo… –dijo Ven rascándose la barbilla.
–Para saber si 2 números son primos entre sí –dijo Sal –Sólo tendremos entonces que comparar entre sí sus divisores, ¿no, Mati?
–Efectivamente –respondió ésta –Pero el problema puede complicarse cuando los números que quieres comparar son muy grandes, Sal.
–¿Cómo se hace con números grandes? –quiso saber el gafotas.
–Pues veréis –empezó a decir Mati –Lo que se hace es calcular el máximo común divisor de esos dos números. Si sale 1, es que son primos. En otro caso, no lo son.
–¿Y cómo se calcula el máximo ése, Mati? –preguntó el pequeño.
–Hay distintas maneras –respondió Mati –Os voy a enseñar el algoritmo de Euclides que es la más sencilla.
–¡Vale! –dijo entusiasmado Ven.
–Para ello vamos a usar sólo numero naturales, ¿vale? –dijo ella.
–¡Vale! –repitió Ven.
–Decidme dos números naturales grandotes y os lo explico con un ejemplo.
Los niños se quedaron pensando muy serios hasta que finalmente Sal propuso:
–¡9876!
–¡Y 3321! –añadió Ven.
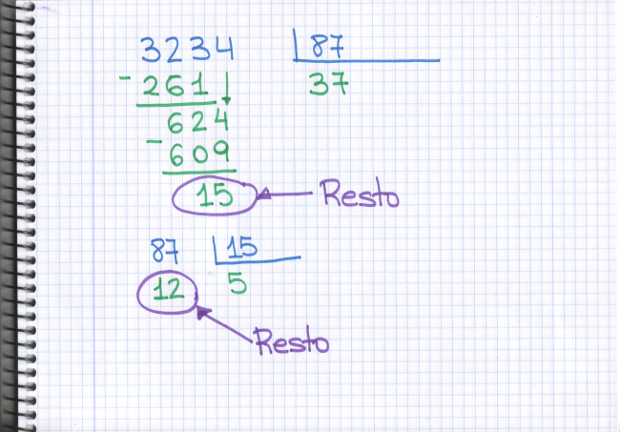
–Muy bien, ahora para calcular el máximo común divisor de estos dos números, al que llamaremos MCD (9876, 3321), lo que hacemos es dividir el mayor, 9876, entre el menor, 3321, y nos fijamos en su resto. Si el resto es 0, MCD(9876,3321) es 3321.
–No, no es 0 el resto, Mati –dijo Sal –¿Qué hacemos?
–Si el resto es distinto de 0, ahora dividimos el divisor, 3321, entre el resto, 3234 –dijo la pelirroja
–Tampoco sale 0 en el resto, Mati…–protestó Ven.
–En esa caso, seguimos –respondió ella –Volvemos a dividir el divisor, 3234, entre el resto, 87.
–No digas nada, Mati –dijo Sal alegre –Ahora dividimos 87 entre 15, ¿no?
–Efectivamente, el divisor entre el resto –respondió la gafotas con un guiño.
–¡Ya lo veo! –dijo el pequeño –Ahora toca 15 entre 12, ¿a que sí?
–¡Sí! –dijo Mati con una gran sonrisa.
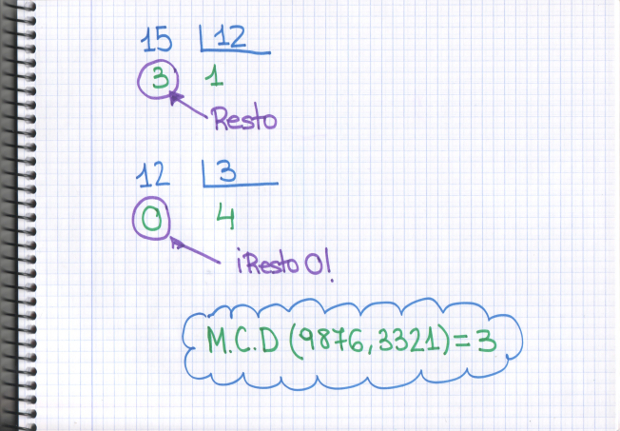
–Ahora dividimos 12 entre 3, ¿no? –preguntó Ven.
–Muy bien, Ven –contestó Mati.
–Y ahora sí que saldrá resto 0, Mati –dijo Sal.
–Efectivamente, eso significa que MCD(9876,3321) es 3, el último resto distinto de 0 que hemos obtenido.
–¡No son primos entre sí! –exclamó Sal.
–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven eufórico –¡Y qué fácil!
–Sí, es cierto, cielo –dijo Mati –Más fácil que como lo hacíamos en mi cole cuando yo era pequeña.
–¿No se había descubierto el algoritmo de Euclides? –preguntó Sal extrañado.
–Huy, sí –respondió la pelirroja –Este algoritmo tiene más de 2000 años de antigüedad…
–¿Dónde están los perros? –preguntó de pronto Ven.
–Creo que el máximo común divisor le dio calor –dio el gafotas riendo –porque se están dando un baño en la piscina ¿Para qué sirve saber si dos números son primos entre sí, Mati?
–Huy, buena pregunta –respondió la pelirroja –Vamos a nadar un poco con los perritos y os lo cuento después.