Anteriormente en Mati, una profesora muy particular…
–¡Moooooooooooooola! –volvió a exclamar el pequeño.
–Sí, mola –corroboró Mati –. La recta de ecuación 2x -3y +1=0 es la gráfica de la función f(x)=(2x+1)/3.
–¿Todas las rectas son gráficas de una función, Mati? –preguntó el gafotas.
–Todas, menos las rectas verticales –dijo ella –. Basta que despejéis, en la ecuación de la recta, el valor de y y lo que os salga es la función de x que estáis representando.
–¡Toma! –exclamó Ven –¡Y lo podremos hacer también con las ecuaciones de las circunferencias!
–¡No! –dijo de pronto Mati –Las circunferencias no son la gráfica de una función, sino de 2 funciones…
–Sí, hombre… –dijo Ven desconfiado. –Piensa un poco –le retó la pelirroja –, a ver si sabes por qué. Pero ahora vamos que es la hora de la función de Sal.
En el capítulo de hoy…
–¿Nos lo cuentas, Mati? –pidió Ven con cara de no haber roto un plato en su vida.
–¿Qué queréis que os cuente, Ven? –dijo ella.
–Por qué dijiste que las circunferencias no son una función como las rectas.
–Ah, eso –exclamó Mati –. Con mucho gusto, caballeros. Os explicaré por qué las circunferencias no son la gráfica de una función.
Sal y Ven sacaron su cuaderno dispuestos a escuchar la explicación de Mati. Gauss no parecía demasiado interesado, la verdad.
–Como os dije la otra tarde –comenzó a decir la pelirroja –, una función es una regla o ley que te permite asignar a cada elemento de un primer conjunto un único elemento de otro conjunto.
–¿Y? –preguntó el gafotas.
–Cuando tenemos una recta, los puntos sobre el eje horizontal, el de abscisas, os lo conté cuando explicamos coordenadas cartesianas, son elementos del primer conjunto –les dijo –, y la función, cuya gráfica está representada por dicha recta, asigna a cada punto del eje de abscisas, o mejor dicho, al valor que representa, la segunda coordenada del único punto sobre la recta que tiene como primera coordenada dicho valor en la abscisa.
Los niños arrugaron sus caritas como pasas. Gauss ladró bajito haciéndose el interesante.
–¿Lo vemos con un ejemplo? –preguntó Mati.
–Por favor –dijo Sal.
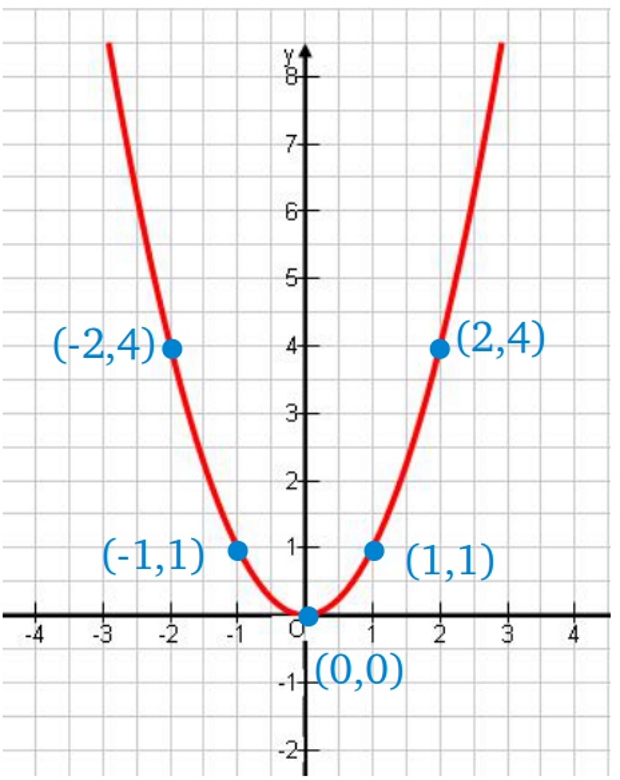
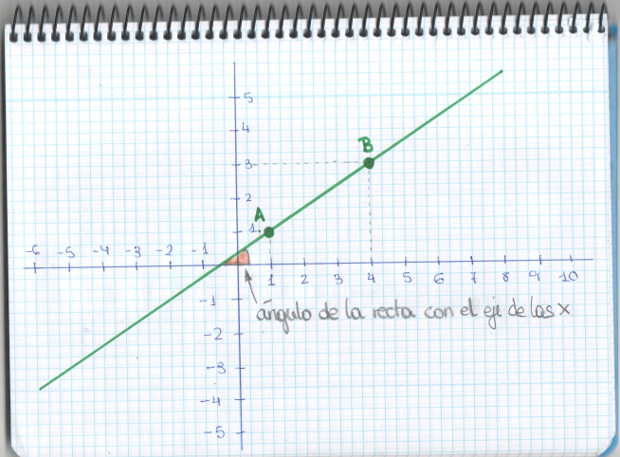
–Vamos a dibujar en nuestros ejes coordenados la recta de ecuación y=2x + 1 –dijo Mati –, que es la gráfica de la función f(x)=2x+1. Para ello solo necesitamos dar 2 valores a x, porque por 2 puntos pasa una única recta. Para x igual a 0, y será 2 por 0 más 1, o sea 1. La recta pasa por el punto (0,1). Para x igual a 1, y será igual a 2 por 1, 2, más 1, o sea 3, la recta pasa por el punto (1, 3).
–Ahora, ya veréis como a cada punto del eje de abscisas –continuó Mati –solo le corresponde un valor de la función f(x)= 2x + 1. Decidme un número.
–¡El 4! –gritó Ven.
–Para calcular el valor que nuestra función asocia al número 4 –dijo ella –o bien sustituimos x por 4 en la función, o bien, trazamos una recta vertical sobre el 4 del eje de abscisas.
–Pintamos la recta vertical que pasa por el 4 –dijo Mati –que en realidad es el punto (4,0) del plano. Esta recta vertical será la recta de ecuación x=4 y vamos a ver cómo sólo corta a nuestra función, la recta verde. en un único punto:
–La corta en el punto (4, 9) –dijo Sal.
–Y sólo en el (4, 9) –añadió Mati –. Eso significa que f(4)=9, es decir, que la función asocia al 4 el valor 9.
–¡Toma, toma, toma! ¡Cómo mola! –exclamó Ven.
–Vamos a ver ahora qué pasa con la circunferencia –les propuso Mati –. Decidme el centro y el radio.
–El centro será el (0,0) –dijo de repente el pequeño.
–Y de radio 5 –añadió el gafotas.
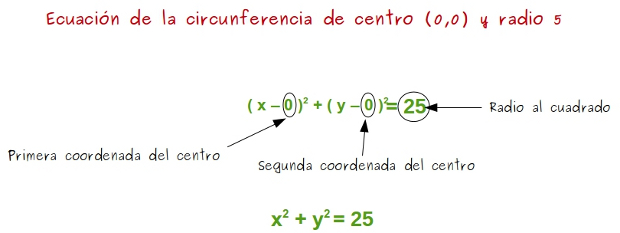
–Vamos a calcular su ecuación como os enseñé –les propuso ella.
–La ecuación es x2 + y2= 25 –dijo Sal.
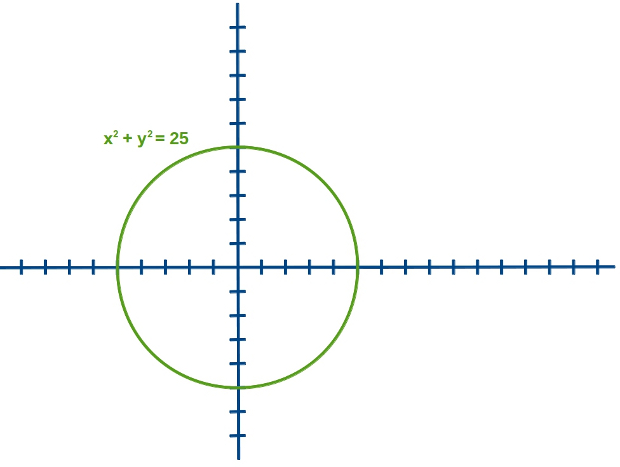
–Ahora la dibujamos en nuestros ejes coordenados –dijo ella.
–Veréis qué pasa si quisiéramos calcular la imagen del 2 –propuso Mati –en la función cuya gráfica es la circunferencia verde. Para ello, como antes, dibujamos la recta vertical sobre el 2, la recta de ecuación x=2.
–¡Toma, toma, toma! ¡Es verdad! –gritó Ven –¡Es verdad!
–¿Y por qué pasa eso? –quiso saber el gafotas.
–Pues verás –empezó diciendo ella –, si despejamos y en la ecuación de la circunferencia nos queda:
–Pero, Mati –dijo Sal –, has conseguido despejar y en la ecuación, entonces ¡es una función!
–No –respondió esta –, porque no da un único valor para cada x…
–¡Anda que no! –dijo Ven.
–Pues no –dijo Mati respondona –¿Cuánto vale la raíz cuadrada de 4?
–¡2! –dijo Sal con entusiasmo.
–O -2 –añadió la pelirroja –Porque -2 al cuadrado también es 4.
–Ah, claro –reconoció el gafotas.
–Si en la ecuación de la circunferencia –continuó ella –sustituimos x por 4, ¿qué ocurre?
–¡Tooooooooooooomaaaaaaaaaaa! –gritó Ven.
–Por eso –dijo Mati –, cuando aparece la raíz cuadrada ponemos delante +√9, -√9 o, incluso ±√9, si queremos indicar que consideramos los 2 posibles valores de la raíz cuadrada.
–Ajá –asintió el gafotas, mientras su hermano seguía mirando el dibujo de la circunferencia de centro (0,0) y radio 5 que habían dibujado en el cuaderno.
–¡Qué pena! –dijo –Tan redondita y no es una función…