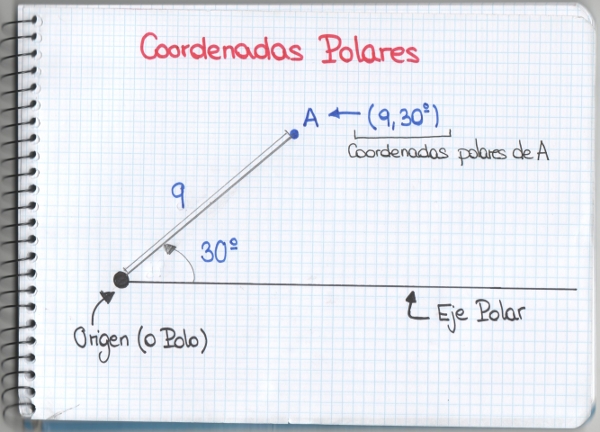
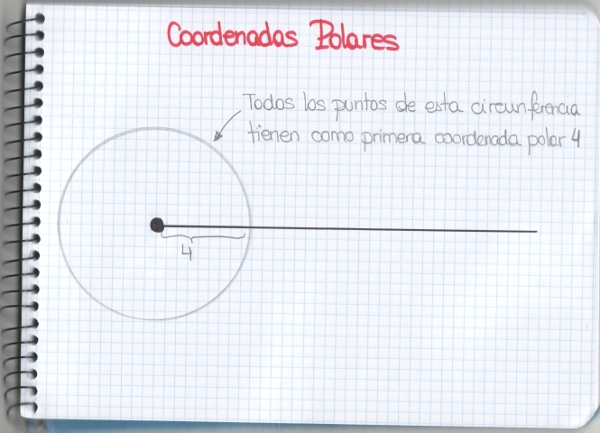
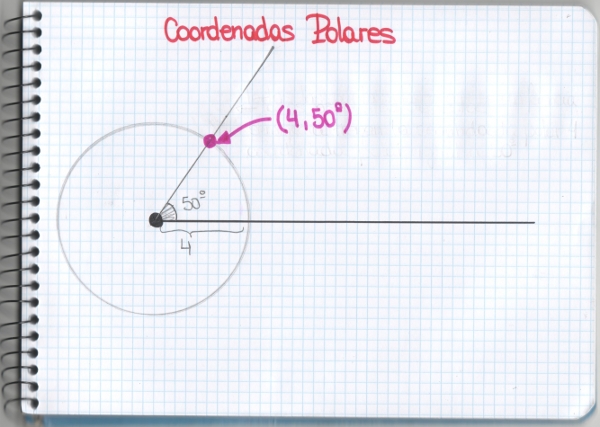
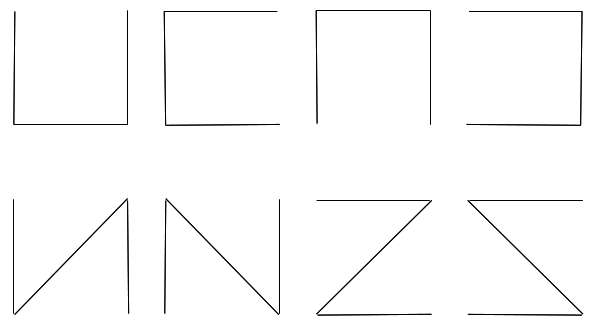Hoy os quisiera plantear un problema de los llamado de optimización, uno de esos problemas que puede parecer, a primera vista, más simple de lo que en realidad es.
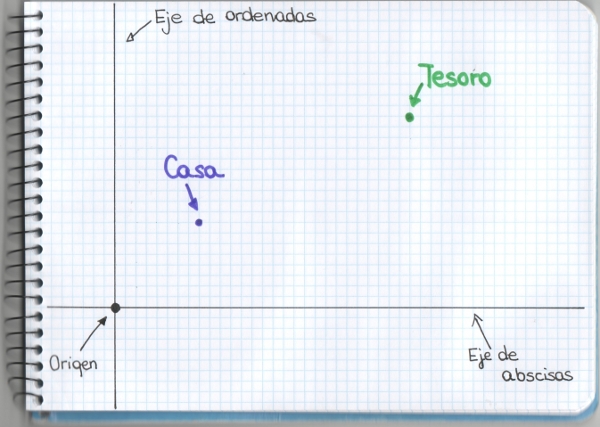
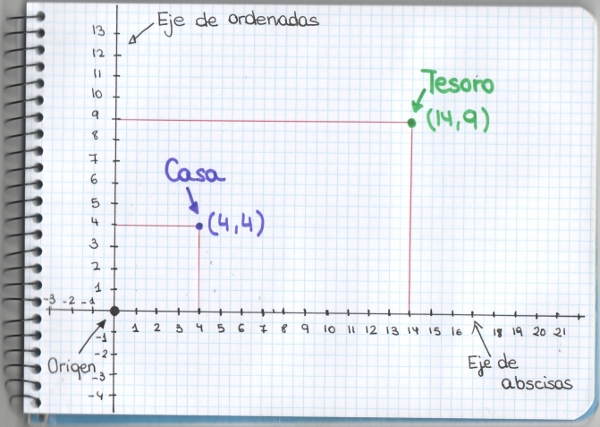
Supongamos que tenemos cuatro pueblos cercanos que, por alguna razón, aún no están comunicados entre sí: igual ha pasado un huracán y ha destruido las carreteras que existían o, peor aún, un banco las ha expropiado y se las ha quedado sin saber qué hacer con ellas. Da igual, el caso es que queremos construir carreteras que las unan y estamos en una suposición, por lo tanto, podemos suponer que no nos sobra el dinero y queremos construir la red de carreteras con menos kilómetros, la más económica. El último dato que nos falta es que las ciudades se encuentran formando un cuadrado de lado 10 km. Así tenemos el siguiente diagrama:
En principio, el problema no parece tan difícil, ya que todas los posibles formas de unir los vértices de un cuadrado usando el menor número de carreteras (segmentos de rectas empezando y terminando en ciudades) son los que presentamos a continuación:
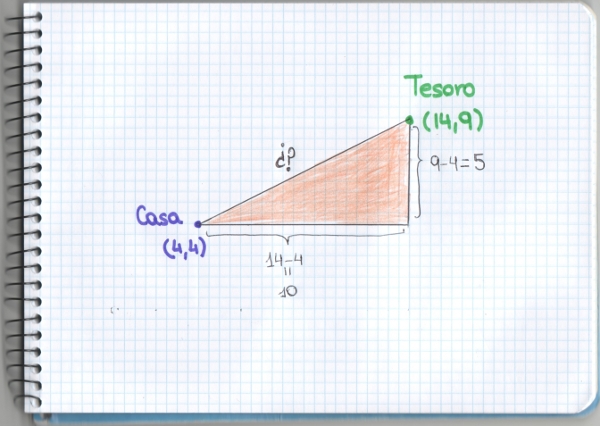
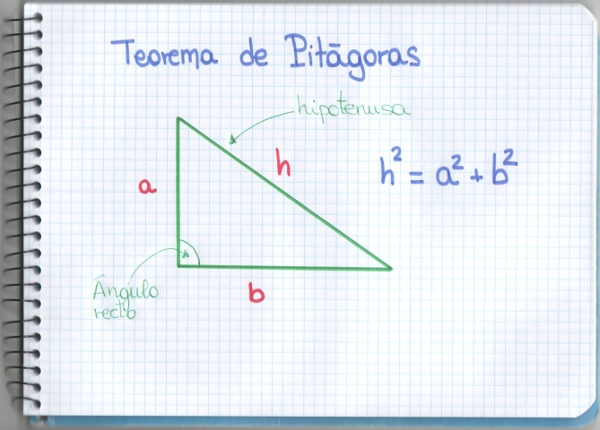
Y se puede comprobar que los de la primera fila suman una distancia total de 30 km, los de la segunda (usando el teorema de Pitágoras) de 20+√200 km que son algo más de 34 km. Así que parece claro que gana cualquiera de los diseños de la primera fila. Pero ¿son esas todas las posibles soluciones?
En principio no, porque hay otros diseños con la misma longitud que los de la primera fila y que presentan algunas ventajas sobre las anteriores, como las dos que presentamos ahora:
Si nos fijamos estos dos diseños tienen también una longitud de 30 km y la ventaja a la que nos referíamos es que la distancia más larga entre los pueblos es más corta que la distancia más larga en aquellos diseños como el que tenía forma de U: para los de forma de U la distancia más larga posible entre dos pueblos es de 30 km, mientras que en el diseño en H la distancia más larga entre dos pueblos es de 20 km.
Pero todavía lo podemos hacer mejor. Si consideramos unir cada par de ciudades diagonalmente opuestas por sendas carreteras con un cruce (o una rotonda si tenemos un alcalde al que le gusten mucho: por aquí por el sur, el de Dos Hermanas, por ejemplo), tendremos un diseño en X:
La longitud total de esa red de carreteras es poco más de 28 km (de nuevo usando Pitágoras). Y parece que ya no se va a poder mejorar, pero estaremos equivocados
Entonces, ¿tenemos diseño ganador? Pues no, porque podemos modificar ligeramente los diseños en H hasta obtener algo así:
Está demostrado que la longitud mínima se alcanza cuando escogemos los puntos de cruce de las carreteras de forma que éstas formen un ángulo de 120º en los puntos en los que se bifurcan.
Es fácil calcular cómo se ha de escoger el punto en el que las carreteras se bifurcan para que sea óptimo el diseño.
Si nos fijamos el triángulo ABC es un triángulo rectángulo (el ángulo en C es de 90º) y el ángulo en B debe ser la mitad de 120º , 60º, por lo tanto, puesto que los ángulos internos de un triángulo suman 180º, tenemos que el ángulo en A (en el triángulo ABC) es de 30º. Si hacemos una copia del triángulo ABC (pegando por el lado AC), y nos fijamos en el triángulo ABB’, éste es un triángulo equilátero (puesto que los ángulos en A, B y B’ son de 60º los 3) y por tanto BC es la mitad de AB, como AC vale 5 km, usando el teorema de Pitágoras tenemos que el lado BC mide 5/ √3 y por lo tanto, obtenemos que la longitud total de esta red de carreteras es de 10+10√3 km que es algo más de 27 km y es el ganador absoluto.
Ahora es el momento en el que planteo: ¿y si en vez de cuatro ciudades son tres todas a la misma distancia? ¿Y cinco?
Si queréis ver la solución a estos problemas, se puede este vídeo maravilloso (está en inglés, pero creo que es suficientemente ilustrativo y muy recomendable), donde se da la solución para los distintos casos, pero lo más interesante es que llega a dicha solución con la única ayuda de unas pompas de jabón. Por cierto, esto me da una idea de la que hablaros otro día: de las matemáticas de las pompas de jabón. Pero eso será en otra ocasión.