–Ya está –dijo Sal y añadió señalando con su dedo –. Ahora solo pinta una línea así.
–¿Así cómo? –preguntó muy serio Ven –. Deberías ser más técnico en tus instrucciones si quieres ser ingeniero aeroespacial.
–¡Puf! Ya estamos… –resopló el gafotas –. Luego dices que soy yo el empollón…
–Es que, como nos explicó Mati –respondió el aludido –, para definir una recta necesitas o dos puntos o un punto y un vector…
–Mira, Ven –dijo de nuevo Sal –, este, este y este. Toma, 3 puntos ¿No querías 2 puntos para tu recta? Pues toma 3, pinta la recta que pasa por esos 3 puntos.
–Bueno, bueno, bueno… –Mati acababa de llegar –Eso no siempre es posible, Sal.

–Hola, Mati –la saludó Sal sin apartar la vista de su diseño.
–Hola, Mati –dijo el pequeño –¿Cómo no vas a poder pintar la recta con 3 puntos? ¿No dijiste que necesitábamos 2? Pues con 3 mucho mejor, hombre.
–No, Ven –dijo ella –. Por 1 punto pasan infinitas rectas, por 2 puntos solo una y por 3, puede que ninguna.
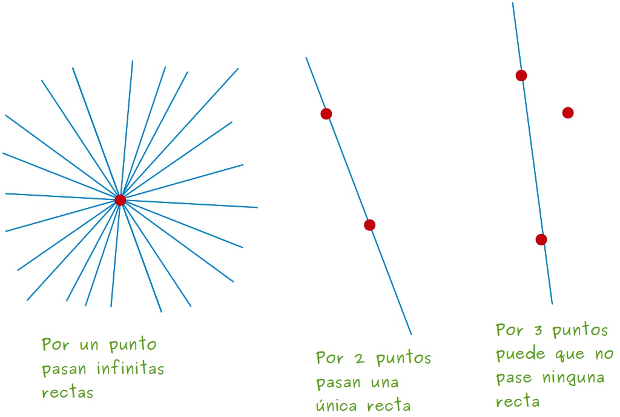
–¡Toma! –aceptó el pequeño –¡Es verdad!
–Claro, Ven –dijo Sal –. Yo ya me había dado cuenta en nuestro dibujo…
Ven miró a su hermano con el ceño fruncido, Gauss resopló.
–Pero, ¿sabes, Ven? –dijo rápidamente Mati para aliviar la tensión ambiental –. Por 3 puntos, siempre pasa una única circunferencia.
–Ya lo sé –dijo el pequeño sin perder de vista a su hermano –, nos lo contaste.
–Tienes razón –dijo la pelirroja –, qué buena memoria tienes.
–Es cierto –añadió Sal queriendo congraciarse con su hermano –, Ven tiene muy buena memoria.
–Mirad –dijo la gafotas –Como ya sabéis lo de la circunferencia y sabéis que una circunferencia no es una función, si queréis os cuento cómo calcular una función cuya gráfica pase por esos 3 puntos. Eso sí, si no tienen la misma abscisa.
–¿Cuál era la abscisa, Mati? –preguntó Ven de repente.
—La abscisa es la coordenada horizontal –dijo Mati –, la que mide la distancia al eje de ordenadas, ¿recuerdas?
–Sí, sí –dijo Ven.
–¿Y por qué no pueden tener la misma abscisa, Mati? –quiso saber el gafotas.
–Porque si queremos que sea una función –respondió ella — para un valor de la x, de la abscisa, no puede tener más de un valor de la y, la ordenada.
–No entiendo –aceptó Ven.
–A ver –siguió ella –No podemos dibujar la gráfica de una función que pase por los puntos (3, 6) y (3, 8), por ejemplo. Porque la segunda coordenada del punto representa el valor de la función, y en este ejemplo, para x igual a 3, tendríamos dos posibles valores de la función, 6 y 8.
–Ah, vale –aceptó el pequeño.
–¿Y cómo será esa función, Mati? –preguntó Sal –¿Será muy rara o parecida a una recta?
–La gráfica de la función que pasa por 3 puntos que no estén alineados, –dijo esta –y que tengan distintas abscisas, será una parábola.
–¡Toma! Esa la conozco –dijo Ven –, es la curva de los tiros parabólicos de fútbol, ¿no?

–Eso es, Ven –dijo Mati -, esa será la forma de nuestra función.
–¿Y cómo sabes que siempre se puede, Mati? –preguntó Sal curioso.
–Porque dados 3 puntos no alineados y con abscisas distintas –respondió ella –, siempre existe un polinomio de grado 2 que pasa por esos 3 puntos, y la gráfica de un polinomio de grado 2 es una parábola.
-¿Un poliqué? –preguntó Ven arrugando la carita.
–Un polinomio –dijo ella –. Una función (de x) que se escribe como suma de potencias (naturales) de x multiplicadas por unos números, que llamamos coeficientes. Mira, te pongo unos ejemplos:

–¿Cómo son esos grados, Mati? –preguntó Ven con cara de pillo —¿Celsius o Fahrenheit?
–No, Ven –respondió la pelirroja –, el grado de un polinomio es el valor de la potencia más alta de x que aparece. En el polinomio f1 la potencia más grande es 4, en el polinomio f2 es 8 y en el polinomio f3 la más grande es 3.
–¡Quietos, parados! –exclamó Ven –Hay números sin potencias de x en los polinomios f1 y f3.
–Sí, es como si x estuviera elevada a 0 -dijo ella –por eso no aparece, por que x elevado a 0 es 1. A esos números que aparecen sin x, se les llama términos independientes, porque como no multiplican a x, no dependerán del valor de esta.

–¿Qué tienen de especial los polinomios, Mati? –preguntó Sal.
–Huy, un montón de cosas –respondió ella –. Son las funciones más simples que hay y, entre otras cosas, se usan para dar valores aproximados de otras funciones mucho más difíciles, pero eso os lo cuento más adelante. Ahora os voy a enseñar a encontrar un polinomio de grado 2, una parábola, que pase por 3 puntos no alineados y con abscisas diferentes.
–¡Venga! –exclamó Ven con alegría.
–Decidme 3 puntos, chicos –pidió Mati.
–A ver… (1,6) –dijo el pequeño –… (2,13)...
–Y (0,3) –apuntó el gafotas.
–Muy bien –dijo ella –. Queremos un polinomio de grado 2, una parábola que pase por estos tres puntos {(0,3), (1,6), (2,13)}. El polinomio que buscamos tiene esa pinta: ax²+bx+c.
–¿Qué son esas letras, Mati? –preguntó Ven.
—¿a, b y c? –preguntó Mati y añadió con voz misteriosa –Son las incógnitas que tenemos que descubrir…
–¿Cómo las descubrimos? –preguntó el gafotas.
–Con un poco de inteligencia -dijo ella guiñando un ojo –. Vamos a ir apuntando las pistas que tenemos:

–¡Toma! –dijo Ven –Parecemos detectives.
–A ver, Ven Holmes –dijo Mati teatrera –¿Qué sabemos de la función?
El pequeño se quedó pensativo y dijo:
–Se le ha visto pasar por (0,3).
–Hum –Mati se rascó la barbilla –Eso significa que f(0) debe valer 3, vamos a sustituir x por 0, a ver qué pasa…

–¿Tenemos más pistas, Sal Poirot? –preguntó Mati.
–Sí, Mati Marple –dijo el gafotas–. También pasó por (1,6).
–Ajá –dijo la pelirroja, eso significa que f(1) es 6.

–Hum, estamos cerca… –dijo Mati –¿Puede aportar algo, Gauss Colombo?
–Guau, guuuuauuuu, guaaaaau
–Dice Colombo que también pasó por (2,13) -dijo Ven divertido.
–Vaya, vaya –dijo ella –, así que f(2) es 13…

–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven.
–Me encanta, Mati –dijo Sal.
–¿Os gusta? –dijo Mati –En realidad, lo que hemos hecho es resolver este sistema de ecuaciones:

–¿También se puede resolver con el método de Gauss que nos enseñaste? –preguntó Sal.
–Efectivamente –respondió ella –, podéis elegir hacerlo como queráis.
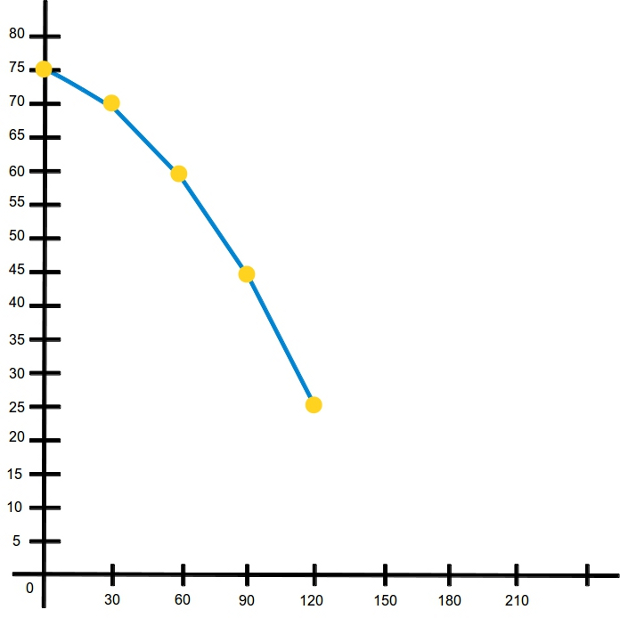
–¿Pintamos la parábola, Mati? –pidió Ven.
–Os tengo que enseñar a dibujar funciones –dijo ella –, pero hoy la dibujamos con Google.

–Es preciosa… –dijo el pequeño Ven.
–Entonces, si tenemos 3 puntos con abscisas diferentes -dijo Sal –, siempre tenemos una parábola.
–Si no están alineados, en cuyo caso sería una recta, –corrigió Mati y añadió con un guiño –,una parábola chafada.
–¿Y si tenemos 4 puntos, Mati? –preguntó el gafotas.
–En ese caso, si repetimos este procedimiento –les contó –llegaremos un polinomio que pase por ellos de grado, como máximo 3. Pero podrá ser de grado 2, y que los 4 estén sobre una parábola, o de grado 1, que estén alineados…
–¡Mola! –dijo Ven.
–A esto –continuó Mati –, a buscar polinomios que pasen por un conjunto de puntos se le llama interpolación polinómica. Otro día os explico para qué se utiliza y otras formas de hacerlo sin resolver sistemas de ecuaciones, ¿vale?
–¡Vale! –exclamó de nuevo Ven.
–¿Y con 5 puntos, Mati? –siguió indagando Sal.
–Con 5 puntos, tendríamos un sistema de 5 ecuaciones con 5 incógnitas, tantas como puntos –respondió esta –, que nos daría como función sospechosa un polinomio de grado, como máximo, 4.
–Claro –dijo el gafotas –, porque si están alineados, será un polinomio de grado 1, una recta…
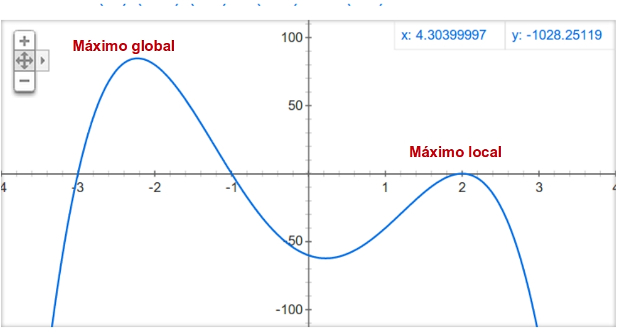
–¿Qué forma tiene un polinomio de grado 4, Mati? –preguntó el pequeño.
–Vamos a mirar uno en Google –les propuso.

–¡Me gustan los polinomios! –gritó Ven.
–Como dice un amigo mío, –dijo Mati con una sonrisa — a mí también, pero solo hasta cierto grado.