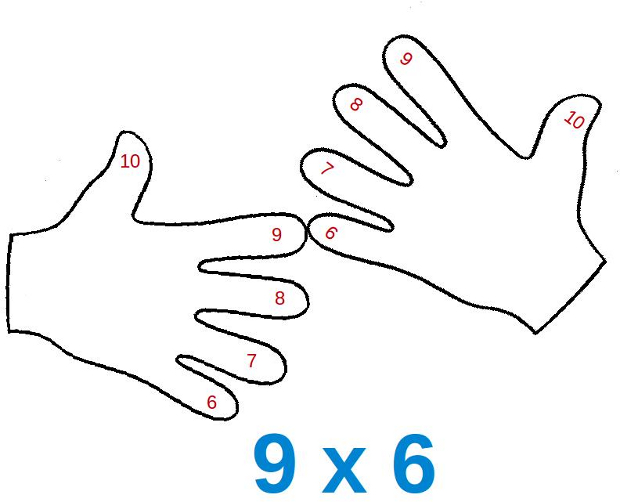
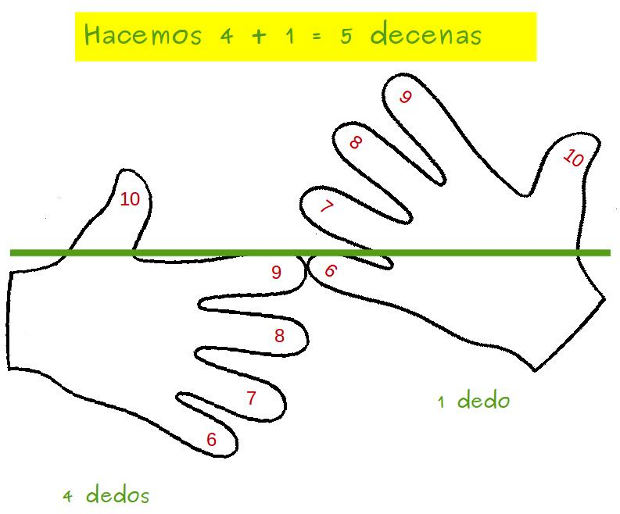
–¡Qué pasada, Mati! –exclamó Ven
–Es el mejor museo del mundo… –corroboró su hermano.
–Bueno, tengo que decir –respondió ella — que sí, que será uno de mis favoritos a partir de ahora.
–¡Y el mío también! –añadió el gafotas
Aprovechando las vacaciones de Navidad, Mati y sus amiguitos han viajado hasta Nueva York para visitar el recién inaugurado Museo de Matemáticas, el MoMath. Un museo lleno de matemáticas con el propósito de mejorar la comprensión y la percepción de éstas, a través de la experimentación y el juego.
–Qué monos los dinosauritos… –dijó Ven –Los quiero para mi habitación.
–Más monos son los monitos, ¿no? –bromeó la pelirroja.
–¿Y el suelo de Voronoi? –le preguntó Sal –¡Eso si que mola todo!
–Es cierto, Sal –dijo Mati –Me resultaría imposible elegir alguna atracción del museo, todas son maravillosas…
–Pues yo lo tengo clarísimo –interrumpió Ven –. Mi favorito es la bici de ruedas cuadradas.
–Huy, sí –confirmó ella –. Me lo he pasado en grande, se deslizaba suave, suave, como si rodara sobre un espejo…
–Es cierto, Mati –dijo el pequeño Ven –. Parece cosa de magia…
–Pero no es magia, Ven –interrumpió su hermano –. Nos lo explicó Mati, ¿recuerdas? Es cosa de la… ¿cómo se llamaba la curva, Mati?
–La catenaria, Sal –respondió ella –. La magia está en que el suelo en el que circula la bicicleta está formado por catenarias invertidas.
–¿Las catenarias son las de los cables? –quiso saber Ven.
–Ajá –confirmó ella — Es la curva que adopta un cable, una cuerda o una cadena, suspendida entre dos extremos. Durante mucho tiempo, se creía que esa curva era un parábola, hasta que finalmente Johann Bernouilli descubrió que no, que era un curva diferente.
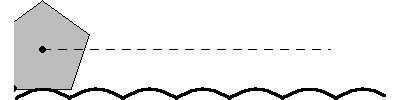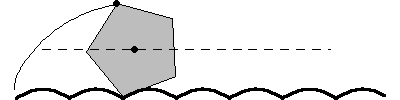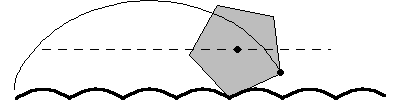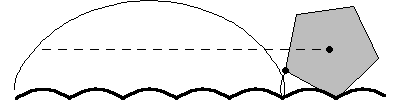
–Pues bien –continuó la pelirroja –El truco está en que para que un movimiento sea suave lo que tenemos que conseguir es que el eje de la rueda, el centro, describa una linea recta. Si la carretera es lisa, eso se consigue únicamente con ruedas circulares, todos los puntos de la rueda están a la misma distancia del centro. Pero esta propiedad no la tiene el cuadrado. Para que la rueda cuadrada ruede manteniendo el centro en línea recta, el suelo no puede ser liso.
–Toma, claro –murmuró Ven.
–Ahora bien –continuó ella –, la rueda cuadrada se desliza manteniendo el centro en línea recta si lo hace sobre un suelo formado por catenarias invertidas.
–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven –¡Ahora lo comprendo todo!
–Es cierto –dijo el gafotas –Recuerdo que nos lo contaste camino de Barcelona…
–Efetivamente, Sal –siguió ella –. Además, con esa misma idea se podrían diseñar bicicletas cn ruedas pentagonales, hexagonales…
–O ruedas con polígonos de Reuleaux, ¿no, Mati? –preguntó el gafotas.
–No, no es lo mismo –dijo ella –En el caso de los polígonos de Reuleaux, el suelo puede ser liso por tener éstos anchura constante.
–Ah, es verdad –Sal se echó las manos a la cabeza y sonrió –. Me he liado un poco.
–Este museo es una pasada… –volvió a decir Ven –Gracias por traernos al MoMath, Mati.
–Sí, gracias, Mati –apoyó Sal –Ha sido una gran idea.
–De nada, chicos –respondió ésta –. En realidad estaba deseando que lo inauguraran desde que Clara me contó que había estado en una exhibición del Momath, un Math Midway, y su amigo George Hart que trabajaba entonces para el MoMath le había invitado a pasear en la bicicleta de ruedas cuadradas e, incluso, a ¡cambiarle la goma de las ruedas a la misma!