Una sucesión de pequeñas voluntades consigue un gran resultado.
Charles Baudelaire
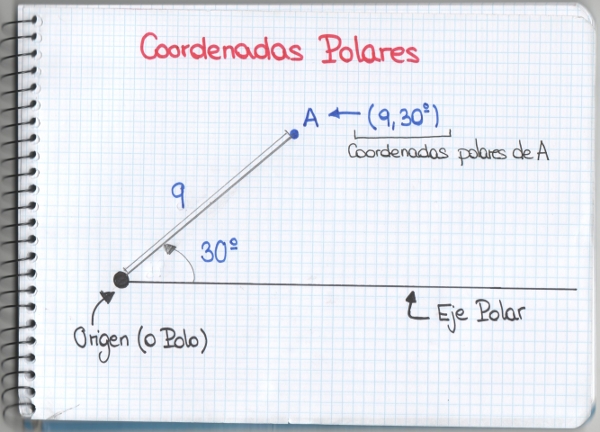
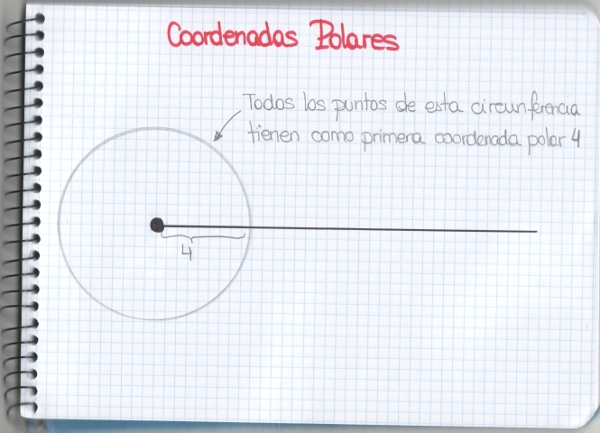
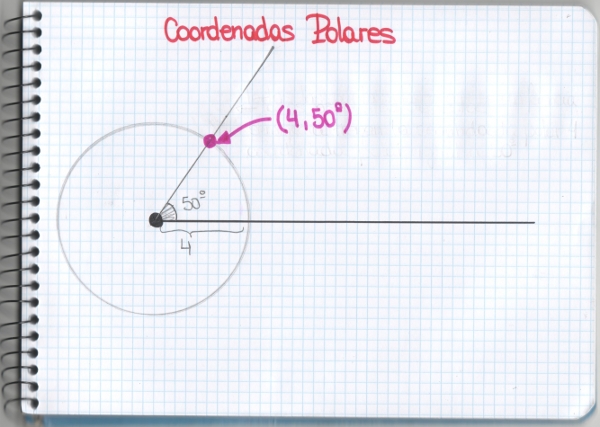
 Para los matemáticos una sucesión es una lista ordenada de objetos o eventos. De hecho, se han estudiado y se estudian las sucesiones con el fin de extraer información de los fenómenos que éstas pueden representar. Alguna de ellas han conseguido bastante fama más allá de los libros de Matemáticas como la sucesión de Fibonacci, de la que Mati y sus amigos ya nos contaron algo. Sí, hablo de Mati en tercera persona, porque hoy ella también salió con los niños y he aprovechado yo, Clara Grima, para asomarme por esta ventana. Como profesora universitaria, como madre de dos niños en educación primaria, como persona preocupada y angustiada por el futuro de la Ciencia en este país… En definitiva, como ciudadana.
Para los matemáticos una sucesión es una lista ordenada de objetos o eventos. De hecho, se han estudiado y se estudian las sucesiones con el fin de extraer información de los fenómenos que éstas pueden representar. Alguna de ellas han conseguido bastante fama más allá de los libros de Matemáticas como la sucesión de Fibonacci, de la que Mati y sus amigos ya nos contaron algo. Sí, hablo de Mati en tercera persona, porque hoy ella también salió con los niños y he aprovechado yo, Clara Grima, para asomarme por esta ventana. Como profesora universitaria, como madre de dos niños en educación primaria, como persona preocupada y angustiada por el futuro de la Ciencia en este país… En definitiva, como ciudadana.
Sin entrar en muchos detalles técnicos, cuando uno tiene una sucesión en matemáticas, una de las primeras cosas que se pregunta es si tiene límite, es decir, si se va acercando cada vez más a un número o al infinito. La de Fibonacci por ejemplo se va a infinito porque crece cada vez más y más en cada término. Otras sin embargo, se acercan cada vez más a cero… Son éstas las que me han inducido a escribir sobre la sucesión de Wert. No, no lo tecleen en el buscador, no me consta que se haya definido esta sucesión.
 Cuando hablo de la sucesión de Wert me refiero, parafraseando a Baudelaire, a la sucesión de voluntades, nada pequeñas en el caso de este señor y el ministerio que representa, que están legislando y modificando el sistema de Educación Pública de este país, a todos los niveles, o la inversión del mismo en proyectos de investigación científica, por ejemplo.
Cuando hablo de la sucesión de Wert me refiero, parafraseando a Baudelaire, a la sucesión de voluntades, nada pequeñas en el caso de este señor y el ministerio que representa, que están legislando y modificando el sistema de Educación Pública de este país, a todos los niveles, o la inversión del mismo en proyectos de investigación científica, por ejemplo.
Nuestro ministro de Educación, Cultura y Deporte ya apuntaba maneras cuando se descolgó diciendo que
Educación para la Ciudadanía se convirtió en una asignatura con una carga de adoctrinamiento.
J. I. Wert Ortega
Para apoyar su tesis el excelente e iluminado señor Wert citó textos de dicha asignatura que nunca se habían llegado a publicar. Da igual, no pasa ná… Para su información, señor Ministro, el adoctrinamiento al que está siendo sometido mi hijo mayor en EPC abarca asuntos como la tolerancia, respeto a los demás, autoestima, empatía, solidaridad… Supongo que habrá oído hablar de estas cosas. No, claro, usted como yo no tuvo la suerte de que en su colegio dedicaran una asignatura a enseñar valores tan importantes, teníamos que rezar. No pasa ná…
En aquel momento, tras la rabia inicial provocada por esta decisión sobre EPC, desde mi punto de vista estúpida, terminé por aceptar que no se trataba más que de un globo sonda, una cortina de humo para que no nos pusiéramos nerviosos esperando el cumplimiento de aquellas promesas electorales que salvarían a nuestro amado país de la crisis económica.
Pero era sólo uno de los primeros términos de la sucesión de Wert… Desde entonces cada término, cada evento de ésta, de la sucesión, no es más que una muestra más de la indudable voluntad de este Ministerio por hacer tender el sistema de Educación en España a la ignorancia del pueblo raso, para que sólo las mejores rentas tengan opción a ofrecer a sus hijos una educación de calidad, desde la educación infantil hasta la universidad. Porque, eso sí, de 0 a 3 años, según este señor, no es educación sino conciliación, lo que demuestra la falta de respeto del mismo hacia la labor desempeñada con entusiasmo y profesionalidad por los educadores encargados de nuestros hijos a estas edades. No pasa ná…
Supongo que a estas alturas todos los que estáis leyendo este artículo conocéis las lindezas propuestas por Wert. No voy a hacer una lista pormenorizada de ellas, sólo un paseíto por ese camino de baldosas amarillas que este señor nos está preparando para volver al sistema de educación pública de aquellos tiempos que tanto parecen añorar. Eso si no nos come antes la bruja del norte, que en este cuento es bastante malvada.
Es cuanto menos gracioso (bueno, no, no tiene ninguna gracia) leer el comienzo del Real Decreto-ley 14/2012, de 20 de abril, de medidas urgentes de racionalización del gasto público en el ámbito educativo.
Las medidas que se adoptan en este real decreto-ley resultan imprescindibles para cumplir con la senda de consolidación fiscal fijada y con el compromiso de reducción de déficit de la Unión Europea,
Se trata, en definitiva, de introducir importantes elementos de racionalidad y eficiencia en el sistema educativo…
¿Imprescindibles? Perdone mi ignorancia, señor Wert, ¿no hay medidas de recortes imprescindibles para la Iglesia, la Casa Real o el ejército? ¿Le parece más racional recortar en Educación que en las tres partidas anteriormente citadas? ¿Saben ustedes qué significa racionalidad? En fin… No pasa ná…
Si uno sigue leyendo el documento, todavía en enseñanza no universitaria, llega a lo de permitir un grado razonable de flexibilidad en el número de alumnos por aula, que supondrá un aumento de la ratio de alumnos por clase. Alto ahí, nada de enfados, que no lo hemos entendido, que lo que vamos a conseguir con ello es que nuestros niños socialicen y se relacionen en la escuela. Veamos, don José Ignacio, nuestros hijos socializan en el parque. Van a la escuela, principalmente a adquirir conocimientos, a afianzar el pensamiento crítico que traen de serie cuando nacen, a satisfacer su curiosidad científica… Que no vayan a clases de hípica no significa que no tengan espacios públicos donde jugar y relacionarse. Lo digo por si no se le había ocurrido.
 No habrá sustituciones para bajas de profesores de menos de 10 días lectivos, o sea, dos semanas de clase. Eso no nos ha explicado el señor Wert para qué le viene bien a nuestros hijos, a ver si lo invitan a alguna tertulia y nos lo cuenta, me tiene en ascuas. Yo, en mi profunda ignorancia como estudiante de la enseñanza pública, lo único que intuyo es que mis hijos pueden pasar hasta 2 semanas de clases sufriendo un desfile de profesores por el aula, profesores de su nivel o no, que apechugarán como mejor puedan durante la hora o las horas que les toque. Es, como ya he dicho, lo que yo puedo intuir de la medida, pero claro, a lo mejor no me entero como soy de la pública… No pasa ná…
No habrá sustituciones para bajas de profesores de menos de 10 días lectivos, o sea, dos semanas de clase. Eso no nos ha explicado el señor Wert para qué le viene bien a nuestros hijos, a ver si lo invitan a alguna tertulia y nos lo cuenta, me tiene en ascuas. Yo, en mi profunda ignorancia como estudiante de la enseñanza pública, lo único que intuyo es que mis hijos pueden pasar hasta 2 semanas de clases sufriendo un desfile de profesores por el aula, profesores de su nivel o no, que apechugarán como mejor puedan durante la hora o las horas que les toque. Es, como ya he dicho, lo que yo puedo intuir de la medida, pero claro, a lo mejor no me entero como soy de la pública… No pasa ná…
Esas y otras ideas en cuanto a la educación no universitaria. Vamos a leer lo que han legislado estos expertos para la Universidad, que ahí no están mis hijos pero es donde curro.
Me tengo que reír, por no llorar, claro. No tienen ni idea. Pero, vamos a ver, seamos serios: ¿cómo vais a regular la carga docente de un profesor universitario en función de los créditos ECTS? Como usted sabe, ¿o no?, el crédito ECTS es una medida de esfuerzo del alumno. En base a eso, la carga docente asignada a los profesores puede variar desde 6 horas por crédito en una Universidad hasta 10 horas por crédito en otras. Ay, vaya, se le ha pasado este detalle… No pasa ná.
Por no hablar de los recortes o incrementos de carga docente al profesor universitario en función de unos criterios específicos de investigación, probablemente confusos para aquellos que no conocen el funcionamiento de la Universidad, que tampoco tienen ni pies ni cabeza. Desde su perspectiva, los peores profesores serán castigados con impartir clases ¿Es eso un mejora para el estudiante? Si los profesores con más sexenios son los más mejores, ¿no deberían éstos impartir más clases? ¿No sería esa una medida para fomentar la investigación de los malos profesores? ¿Cómo se detectan a esos malos profesores?
Os enlazo la opinión de cinco profesores universitarios: Alberto Márquez, Pablo Mira, JoseRa Portillo (aka Zifra) y Joaquín Sevilla y este otro por si queréis profundizar en el asunto.
Ya tenemos a los profesores controladitos, vamos ahora a por los estudiantes de la Universidad
¿Qué piensa, señor Ministro? ¿Qué podemos hacer para que el que «tenga talento y ganas de estudiar» pueda hacerlo «en cualquier nivel»? Pues nada, subamos las tasas, reduzcamos la partida para becas y endurezcamos los requisitos para concederlas (insertar aquí una risa de malvado de opereta) ¿Y si una familia no puede permitirse enviar a su hijo a la Universidad en esas condiciones? Ah, que concederán créditos. Espero que haya hecho usted mejor estas cuentas y que no le pase como cuando contó el número de universidades de California… Eso si la familia de verdad tiene dificultades para enviar a sus hijos a la universidad, porque el iluminado también se pregunta si «no se tienen recursos o no se quieren dedicar en detrimento de dedicarlos a otra cosa». O sea, que además de pobres somos mentirosos.
Llegados a este punto de desánimo, sólo nos queda por mirar cómo se está tratando a la Ciencia para entender la sucesión completa ¿Para qué queréis ir a la Universidad, niños y niñas? ¿Para tener que salir fuera de este país para poder investigar si os decantáis por esa opción? ¿No veis que ya el Gobierno de Castilla-La Mancha ha suprimido la financiación de «todos los programas de investigación» de la Universidad de esta comunidad? ¿O es que además de pobres sois ingenuos?
Sepa usted, don José Ignacio, que sin ciencia, no hay futuro. Pero no pasa ná…
No, no me diga señor Wert que son medidas coyunturales y temporales porque mi hijo es único, como lo son todos los niños que se verán afectados, y lo que él no aprenda estos años, la calidad de enseñanza que él no tenga estos años, no se la van a devolver nunca ¿O tiene previsto dar clases particulares para recuperar una vez que su gobierno nos traiga esa bonanza económica que nos prometieron?
Si uno analiza con detalle toda esta sucesión de medidas del Ministerio de Educación, Cultura y Deporte sólo le quedan dos posibles explicaciones: o son tan ignorantes que no se dan cuenta del mal que están haciendo o son tan malintencionados que quieren embrutecer al pueblo para manejarlo mejor. En cualquiera de los dos casos, me inquieta que estén gobernando este país con mayoría absoluta.
Y mi inquietud no disminuye cuando descubro que están consiguiendo lanzar un mensaje a la población al más puro estilo Divide y Vencerás. Porque aunque lo lógico en esta situación, creo, sería que hiciésemos piña contra el atropello, tienes que oír en la calle frases del estilo de «los maestros viven demasiado bien», «40 éramos en mi clase y no pasaba nada», «los científicos están en la nómina de las farmacéuticas», «si no se quieren ir a Alemania a investigar, que se vayan a Lepe a coger fresas», «menos universidad y más pico y pala»... Algunos con hijos en escuelas públicas, otros con familiares en proceso de curación de un cáncer… Me recuerda inevitablemente a aquella película en la que el pueblo discutía si deberían crear el Frente Popular de Judea o el Frente Judaico Popular mientras seguían gobernando los romanos. No pasa ná…
¿No pasa ná?
Termino como empecé, con la misma cita de Baudelaire ¿Y si somos nosotros los que creamos una sucesión de pequeñas voluntades que contrarreste la sucesión de Wert? Porque intuyo que ésta tiende a cero.
Una sucesión de pequeñas voluntades consigue un gran resultado.
Charles Baudelaire