La semana pasada la terminamos con una noticia tan gratificante como ésta. Y una se plantea ¿quién está decidiendo nuestros destinos? ¿Quién está dibujando el futuro de nuestras familias? ¿Cuántos nos están vigilando? Y porque sospecho, digo sospecho, que también nos vigilan desde ese polígono de 5 vértices, el Pentágono, se me ha venido a la cabeza uno de mis problemas favoritos de Geometría Computacional que mezcla esos dos conceptos, vigilancia y polígonos: El problema de la Galería de Arte. Aparte de la belleza intrínseca de este problema, de la que intentaré convenceros a lo largo de esta entrada, mi debilidad por él tiene un origen romántico: fue el primer problema de esta disciplina que leí y que me atrapó en las redes de esta forma de hacer Matemáticas.
¿Cuál es el Problema de la Galeria de Arte?
El problema fue planteado por Victor Klee en 1973, pero antes de plantearlo, dejadme que demos algunas nociones muy sencillitas. Vamos a hablar de galerías de artes, museos, que tenemos que vigilar para que nadie toque ni se lleve nada. Pues bien, para nosotros, en esta versión del problema que vamos a contar (hay muchísimas variantes), la galería que queremos vigilar estará representado por un polígono simple, y cuando decimos simple lo que queremos decir es que los lados de nuestro polígono no se cortan entre ellos, voy a hacer un dibujo por si se ve más claro.
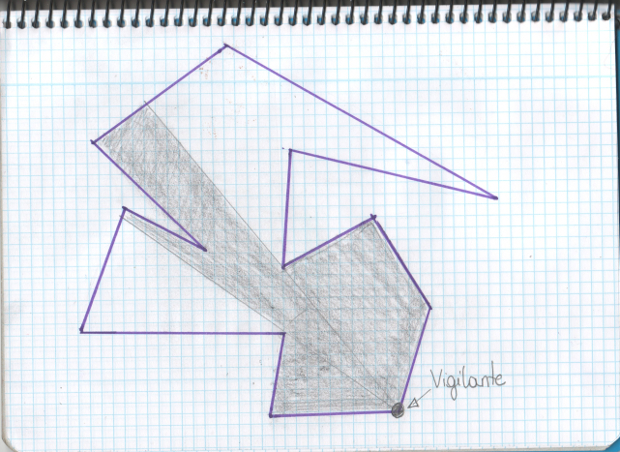
Seguimos. Cuando decimos que queremos vigilar la galería de arte, lo que queremos es decidir dónde colocaremos a los vigilantes en el polígono que representa a la galería con el fin de que toda ella quede cubierta por la mirada de éstos. En esta primera versión del problema, los vigilantes tienen que estar situados en los vértices (esquinas) del polígono, fijos, no se pueden mover. Tienen visión de 360ª y no son miopes, es decir, pueden ver a cualquier distancia, siempre que no haya una pared que se lo impida. A ver, voy a hacer otro dibujo por aquello de que una imagen….
En la imagen superior, hemos situado un vigilante en un vértice del polígono y hemos sombreado la zona que sería cubierta por éste, sin moverse, suponiendo que puede ver a cualquier distancia y 360º a la redonda. Con estas restricciones, ya podemos plantear la pregunta que planteó Klee:
Dado un polígono con N vértices ¿cuántos vigilantes son siempre suficientes para vigilar todo el polígono?
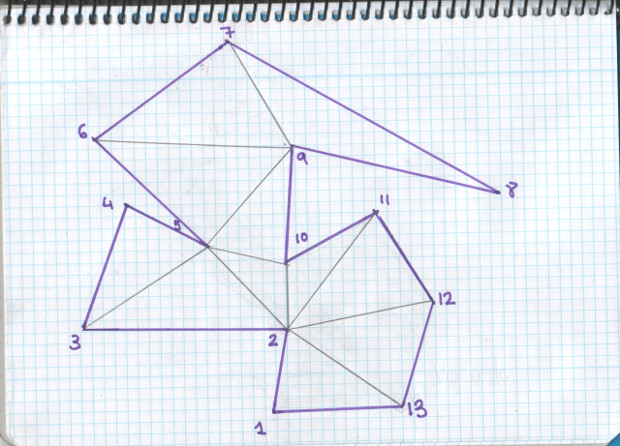
Ahora bien, el problema que plantea Klee no es que nos dan un polígono, dibujado, con N vértices y que nosotros coloquemos el menor número de vigilantes para ese polígono en concreto. Lo que plantea Klee es que demos una fórmula o relación, de forma que podamos saber para un número de vértices N cualquiera, cuántos guardianes serán suficientes para vigilar esa galería, sin saber siquiera qué forma tiene la galería, sólo a partir del numero de vértices que tiene el polígono que representa la planta del museo. Pero, ¿eso como va a ser? La forma del polígono tiene mucho que ver, de hecho puede haber polígonos con muchos vértices que se vigilen con un sólo vigilante y otros que con muchos menos necesiten más de uno… Otro dibujo nos vendrá bien.
En el dibujo anterior, tenemos una galería con 13 vértices que puede ser vigilada por un sólo guardián y otra con 6 vértices, que va a necesitar 2. Entonces, ¿cómo vamos poder dar un número en función del número de vértices? Si pensamos en un hexágono regular, podemos entender que será vigilado con 1 sólo vigilante, y el polígono de 6 lados de nuestra anterior figura necesita 2, ¿cómo vamos a encontrar esa fórmula?
Pues sí, se encontró. Bueno, la relación que encontró Chvátal en 1975, es que cualquier galería de N vértices, sea como sea, con la forma que sea, por muy enrevesado que sea el Calatrava de turno, se puede vigilar siempre con N/3 guardianes. En realidad, más concretamente, con la parte entera por defecto de ese número, que escribimos así ⌊N/3⌋, esto es, que si N/3 no nos sale un número natural, sino que sale con decimales, nos quedamos con ése mismo número pero sin decimales, nada de poner trozos de vigilantes, eso lo dejamos para Dexter y otros como él. Por ejemplo, cualquier galería de 13 vértices, sea como sea, necesitará como máximo, 4 vigilantes (13/3 = 4’33333333…) Que sí, que la del último dibujo necesita sólo 1, vale, pero no es posible encontrar ninguna que necesite más de 4, eso es lo que nos asegura el Teorema de la Galería de Arte de Chvátal. Eso y que siempre es posible encontrar un polígono de N vértices que necesite exactamente ⌊N/3⌋ guardianes.
Pues bien, aunque el mérito de encontrar la fórmula que relacionara el número de vértices del polígono con el número máximo de guardianes que se necesitarían para vigilarlo es de Chvátal, ha sido la demostración de este hecho dada por Fisk en 1978 la que más ha trascendido por su elegancia y sencillez. Tanto que ha sido una de las elegidas para aperecer en el Libro de las Demostraciones del que tanto hablaba Erdős y del también hablamos aquí.
Vamos a contar la demostración de Fisk porque es concisa, sencilla, brillante y hermosa.
Lo primero que observa Fisk es que un triángulo, sea como sea, sólo necesita siempre un vigilante en uno de sus vértices, ¿verdad? Pues lo que propone hacer es dividir la galería en triángulos, asegurar la vigilancia en cada unos de esos triángulos y con ello tendrá asegurada la vigilancia del polígono completo. Vamos allá…
En primer lugar, lo que hay que hacer es triangular el polígono ¿Cómo? Añadiendo diagonales interiores uniendo vértices no consecutivos del polígono, siempre que no corten a otra diagonal ya dibujada o a la frontera del polígono.
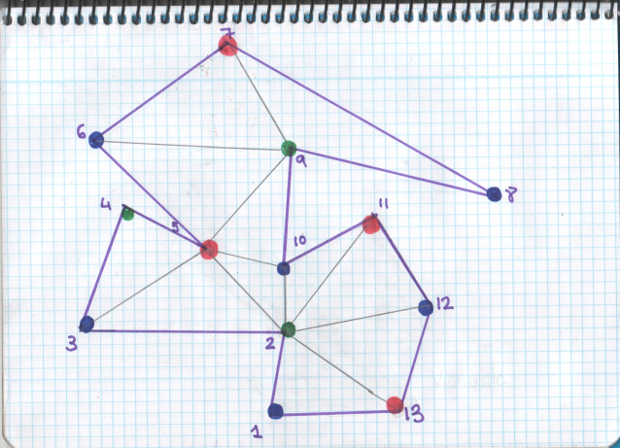
Ahora vamos a asignar colores a los vértices del polígono respetando únicamente una regla: dos vértices con el mismo color no pueden estar unidos en el dibujo de la triangulación que hemos hecho del polígono. Pues bien, respetando esta regla, Fisk demuestra que se puede colorear la triangulación del polígono con 3 y sólo 3 colores.
Venga. Ahora contamos cuántos vértices hay de cada uno de los 3 colores en la triangulación del polígono. En el ejemplo que estamos haciendo en nuestro cuaderno, tenemos 6 vértices azules, 4 vértices rojos, y 3 vértices verdes. Elegimos el color menos popular de los 3, en esto caso el verde, y colocamos un vigilante en cada uno de los 3 vértices verdes y ¡tachán! Ya está todo el polígono vigilado ¿Por qué? Pues porque todos los triángulos del polígono tienen que tener un vértice verde (en realidad, todos los triángulos tienen un vértice de cada uno de los colores) y como en todos los vértices verdes hay un vigilante, todos los triángulos estarán vigilados.
Sí, es maravillosa la demostración. Yo también me quedé boquiabierta la primera vez que la leí.
Bueno, nos queda apuntar un detalle ¿Cómo sabemos que el color menos popular de la triangulación siempre aparece como máximo ⌊N/3⌋ veces? Pues por el Prinicipio del palomar. Supongamos que los vértices son palomas y los colores, 3 palomares. Asignar colores a los N vértices se puede interpretar como asignar las N palomas a uno de los 3 palomares. Pues ya está, uno de los 3 palomares como mucho, tiene N/3 palomas. Porque si los tres tuvieran más de N/3 palomas, la suma de las 3 cantidades sería superior a N.
 Lo que sabemos entonces a partir de este teorema es que sea como sea el polígono de N vértices que nos propongan, como máximo, vamos a necesitar ⌊N/3⌋ vigilantes para vigilarlo. Eso sí, hay veces que necesitaremos muchos menos, y otra en que necesitaremos exactamente ⌊N/3⌋.
Lo que sabemos entonces a partir de este teorema es que sea como sea el polígono de N vértices que nos propongan, como máximo, vamos a necesitar ⌊N/3⌋ vigilantes para vigilarlo. Eso sí, hay veces que necesitaremos muchos menos, y otra en que necesitaremos exactamente ⌊N/3⌋.
Este problema de la Galería de Arte ha dado lugar a una inmensa cantidad de problemas geométricos relacionados, simplemente con modificar algunas de las condiciones: permitiendo que los vigilantes se muevan, obligando a que cada vigilante esté controlado por otro de sus compañeros en todo momento, restringiéndose a un ángulo de visibilidad (pensando en focos e iluminación), permitiendo que se atraviesen paredes (si pensamos en routers)… Todos problemas muy sencillos de plantear pero la mayoría muy difíciles de resolver.
Lo dejamos por aquí y espero que haya servido para olvidar durante un rato cuántos y quiénes son los que nos están vigilando a todos nosotros…