2012 | Mati, una profesora muy particular

Archivo de 2012

¿Cuántos nos están vigilando?

18 de junio de 2012

La semana pasada la terminamos con una noticia tan gratificante como ésta. Y una se plantea ¿quién está decidiendo nuestros destinos? ¿Quién está dibujando el futuro de nuestras familias? ¿Cuántos nos están vigilando? Y porque sospecho, digo sospecho, que también nos vigilan desde ese polígono de 5 vértices, el Pentágono, se me ha venido a la cabeza uno de mis problemas favoritos de Geometría Computacional que mezcla esos dos conceptos, vigilancia y polígonos: El problema de la Galería de Arte. Aparte de la belleza intrínseca de este problema, de la que intentaré convenceros a lo largo de esta entrada, mi debilidad por él tiene un origen romántico: fue el primer problema de esta disciplina que leí y que me atrapó en las redes de esta forma de hacer Matemáticas.

¿Cuál es el Problema de la Galeria de Arte?

El problema fue planteado por Victor Klee en 1973, pero antes de plantearlo, dejadme que demos algunas nociones muy sencillitas. Vamos a hablar de galerías de artes, museos, que tenemos que vigilar para que nadie toque ni se lleve nada. Pues bien, para nosotros, en esta versión del problema que vamos a contar (hay muchísimas variantes), la galería que queremos vigilar estará representado por un polígono simple, y cuando decimos simple lo que queremos decir es que los lados de nuestro polígono no se cortan entre ellos, voy a hacer un dibujo por si se ve más claro.

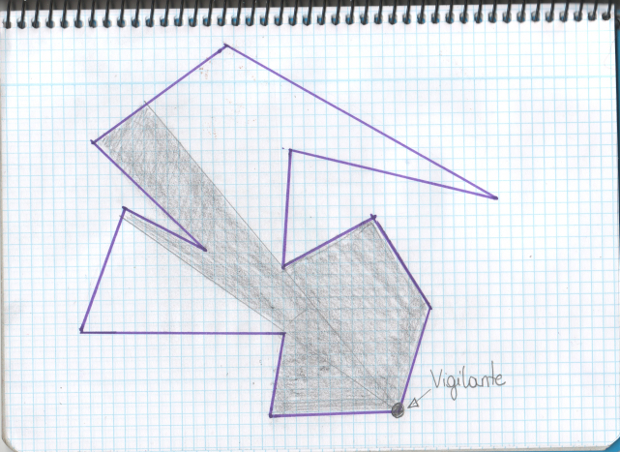
Seguimos. Cuando decimos que queremos vigilar la galería de arte, lo que queremos es decidir dónde colocaremos a los vigilantes en el polígono que representa a la galería con el fin de que toda ella quede cubierta por la mirada de éstos. En esta primera versión del problema, los vigilantes tienen que estar situados en los vértices (esquinas) del polígono, fijos, no se pueden mover. Tienen visión de 360ª y no son miopes, es decir, pueden ver a cualquier distancia, siempre que no haya una pared que se lo impida. A ver, voy a hacer otro dibujo por aquello de que una imagen….

En la imagen superior, hemos situado un vigilante en un vértice del polígono y hemos sombreado la zona que sería cubierta por éste, sin moverse, suponiendo que puede ver a cualquier distancia y 360º a la redonda. Con estas restricciones, ya podemos plantear la pregunta que planteó Klee:

Dado un polígono con N vértices ¿cuántos vigilantes son siempre suficientes para vigilar todo el polígono?

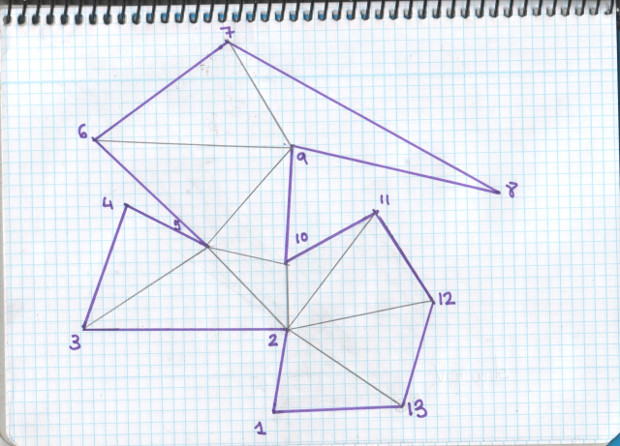
Ahora bien, el problema que plantea Klee no es que nos dan un polígono, dibujado, con N vértices y que nosotros coloquemos el menor número de vigilantes para ese polígono en concreto. Lo que plantea Klee es que demos una fórmula o relación, de forma que podamos saber para un número de vértices N cualquiera, cuántos guardianes serán suficientes para vigilar esa galería, sin saber siquiera qué forma tiene la galería, sólo a partir del numero de vértices que tiene el polígono que representa la planta del museo. Pero, ¿eso como va a ser? La forma del polígono tiene mucho que ver, de hecho puede haber polígonos con muchos vértices que se vigilen con un sólo vigilante y otros que con muchos menos necesiten más de uno… Otro dibujo nos vendrá bien.

En el dibujo anterior, tenemos una galería con 13 vértices que puede ser vigilada por un sólo guardián y otra con 6 vértices, que va a necesitar 2. Entonces, ¿cómo vamos poder dar un número en función del número de vértices? Si pensamos en un hexágono regular, podemos entender que será vigilado con 1 sólo vigilante, y el polígono de 6 lados de nuestra anterior figura necesita 2, ¿cómo vamos a encontrar esa fórmula?

Pues sí, se encontró. Bueno, la relación que encontró Chvátal en 1975, es que cualquier galería de N vértices, sea como sea, con la forma que sea, por muy enrevesado que sea el Calatrava de turno, se puede vigilar siempre con N/3 guardianes. En realidad, más concretamente, con la parte entera por defecto de ese número, que escribimos así ⌊N/3⌋, esto es, que si N/3 no nos sale un número natural, sino que sale con decimales, nos quedamos con ése mismo número pero sin decimales, nada de poner trozos de vigilantes, eso lo dejamos para Dexter y otros como él. Por ejemplo, cualquier galería de 13 vértices, sea como sea, necesitará como máximo, 4 vigilantes (13/3 = 4’33333333…) Que sí, que la del último dibujo necesita sólo 1, vale, pero no es posible encontrar ninguna que necesite más de 4, eso es lo que nos asegura el Teorema de la Galería de Arte de Chvátal. Eso y que siempre es posible encontrar un polígono de N vértices que necesite exactamente ⌊N/3⌋ guardianes.

Pues bien, aunque el mérito de encontrar la fórmula que relacionara el número de vértices del polígono con el número máximo de guardianes que se necesitarían para vigilarlo es de Chvátal, ha sido la demostración de este hecho dada por Fisk en 1978 la que más ha trascendido por su elegancia y sencillez. Tanto que ha sido una de las elegidas para aperecer en el Libro de las Demostraciones del que tanto hablaba Erdős y del también hablamos aquí.

Vamos a contar la demostración de Fisk porque es concisa, sencilla, brillante y hermosa.

Lo primero que observa Fisk es que un triángulo, sea como sea, sólo necesita siempre un vigilante en uno de sus vértices, ¿verdad? Pues lo que propone hacer es dividir la galería en triángulos, asegurar la vigilancia en cada unos de esos triángulos y con ello tendrá asegurada la vigilancia del polígono completo. Vamos allá…

En primer lugar, lo que hay que hacer es triangular el polígono ¿Cómo? Añadiendo diagonales interiores uniendo vértices no consecutivos del polígono, siempre que no corten a otra diagonal ya dibujada o a la frontera del polígono.

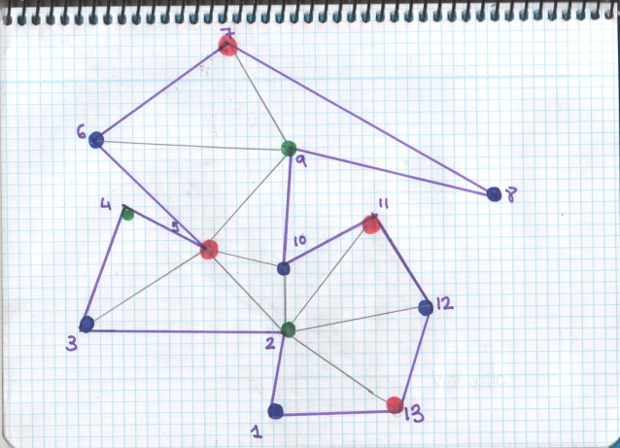
Ahora vamos a asignar colores a los vértices del polígono respetando únicamente una regla: dos vértices con el mismo color no pueden estar unidos en el dibujo de la triangulación que hemos hecho del polígono. Pues bien, respetando esta regla, Fisk demuestra que se puede colorear la triangulación del polígono con 3 y sólo 3 colores.

Venga. Ahora contamos cuántos vértices hay de cada uno de los 3 colores en la triangulación del polígono. En el ejemplo que estamos haciendo en nuestro cuaderno, tenemos 6 vértices azules, 4 vértices rojos, y 3 vértices verdes. Elegimos el color menos popular de los 3, en esto caso el verde, y colocamos un vigilante en cada uno de los 3 vértices verdes y ¡tachán! Ya está todo el polígono vigilado ¿Por qué? Pues porque todos los triángulos del polígono tienen que tener un vértice verde (en realidad, todos los triángulos tienen un vértice de cada uno de los colores) y como en todos los vértices verdes hay un vigilante, todos los triángulos estarán vigilados.

Sí, es maravillosa la demostración. Yo también me quedé boquiabierta la primera vez que la leí.

Bueno, nos queda apuntar un detalle ¿Cómo sabemos que el color menos popular de la triangulación siempre aparece como máximo ⌊N/3⌋ veces? Pues por el Prinicipio del palomar. Supongamos que los vértices son palomas y los colores, 3 palomares. Asignar colores a los N vértices se puede interpretar como asignar las N palomas a uno de los 3 palomares. Pues ya está, uno de los 3 palomares como mucho, tiene N/3 palomas. Porque si los tres tuvieran más de N/3 palomas, la suma de las 3 cantidades sería superior a N.

Lo que sabemos entonces a partir de este teorema es que sea como sea el polígono de N vértices que nos propongan, como máximo, vamos a necesitar ⌊N/3⌋ vigilantes para vigilarlo. Eso sí, hay veces que necesitaremos muchos menos, y otra en que necesitaremos exactamente ⌊N/3⌋.

Este problema de la Galería de Arte ha dado lugar a una inmensa cantidad de problemas geométricos relacionados, simplemente con modificar algunas de las condiciones: permitiendo que los vigilantes se muevan, obligando a que cada vigilante esté controlado por otro de sus compañeros en todo momento, restringiéndose a un ángulo de visibilidad (pensando en focos e iluminación), permitiendo que se atraviesen paredes (si pensamos en routers)… Todos problemas muy sencillos de plantear pero la mayoría muy difíciles de resolver.

Lo dejamos por aquí y espero que haya servido para olvidar durante un rato cuántos y quiénes son los que nos están vigilando a todos nosotros…

Tags: Chvátal, Coloración, Erdős, Fisk, Geometría Computacional, Principio del palomar, Teorema de la Galería de Arte, Triangulaciones | Almacenado en: Ahora que los niños salieron a jugar...
12 comentarios

Más o menos probable…

13 de junio de 2012

–¡Cara! ¡Saco yo!

–¡No vale! ¡Ha rebotado en Gauss! –Ven estaba un poco mosqueado.

–¿Otra vez? ¿Y eso qué más da, Ven?

–Se repite. Ah, se siente…

–¡Cara! ¡Saco yo! –gritó Sal de nuevo.

–No, no vale –respondió Ven, mientras Gauss resoplaba con cansancio.

–Y ahora, ¿qué pasa? –protestó el gafotas.

–No me fío de esa moneda, la has cogido de tu hucha…

–Vamos, Ven –bufó Sal –No tengo ninguna moneda falsa en mi hucha…

–¿Cómo lo sabes? –inquirió el pequeño –¿Los has comprobado como nos enseñó Mati?

–No, no lo he comprobado, Ven –respondió Sal aburrido –Pero son todas verdaderas, como las tuyas…

–¿Qué les pasa a estos chicos? –Mati acababa de llegar.

–Hola, Mati –la saludó Sal.

–Hola, Sal me quiere hacer trampa con la moneda –dijo el pequeño.

–Pesado… –bufó Sal.

–¿Por qué crees que Sal te quiere hacer trampas, Ven?

–Porque ha traído una moneda que siempre sale cara… –contestó éste.

–Eso no es verdad, Ven –se defendió Sal –Ha sido casualidad.

–Vamos a ver –intentó mediar Mati –¿Queréis que os cuente algo sobre lanzamientos de monedas y probabilidad?

–¡Sí! –contestaron los dos a la vez. Gauss resopló aliviado. Mati sacó su libreta.

–Vamos a aprender primero cómo se calcula la probabilidad de que salga cara en la moneda usando la regla de Laplace –comenzó a contarles la pelirroja.

–En el caso del lanzamiento de una moneda y calcular la probabilidad de obtener cara –siguió –el número de casos favorables es 1, que salga cara, y el número de casos posibles es 2, cara y cruz.

–Y sale 1/2 –dijo Ven –La mitad, eso ya lo sabíamos, Mati, el 50% de posibilidades…

–Sí, lo sé –afirmó ella –Con las monedas es muy fácil, pero sirve para todo. Por ejemplo, si lanzamos un dado, ¿cuál es la probabilidad de obtener una potencia de 2?

–Yo lo hago en la libreta, Mati –se apresuró a decir Sal

–Sí, pero ¿por qué no calculas la probabilidad de que Sal saque cuatro caras seguidas? –pidió Ven a la pelirroja.

–Vale, vamos a hacer un diagrama con todas los posibles resultados del lanzamiento de una moneda 4 veces –les dijo.

–Si empezamos en el punto azul y caminamos sobre las aristas azules, tenemos todos los resultados, ¿no?

–A ver… –dijo Ven señalando con su dedo sobre el diagrama —Cara, cruz, cruz, cruz… Y por aquí, cruz, cara, cara, cara...

–Si, Ven –interrumpió su hermano –Están todas.

–Ahora bien, en cada tirada, la probabilidad de obtener cara o cruz es siempre 1/2, ¿no? –continuó ella –Lo escribimos sobre las ramas.

–Bueno, chicos, ¿cuántos casos posibles hay? –preguntó Mati –Sólo tenéis que contar la columna de la derecha, cada una corresponde a un resultado posible.

–¡16! –dijo Ven con entusiasmo.

–¿Y caso favorables para obtener 4 caras? –siguió preguntando la pelirroja.

Los niños estuvieron mirando el cuaderno…

–Sólo uno, Mati –señaló Sal — Sólo cuando sale cara, cara, cara, cara.

–Entonces la probabilidad de obtener 4 caras es… –Mati dejaba la pregunta en el aire.

–¡1/16! –dijeron los 2 hermanos a la vez.

–Efectivamente, chicos –corroboró Mati –Y si os fijáis, 1/16 es el resultado de multiplicar las probabilidades que nos vamos encontrando por el camino hasta llegar al cuarto lanzamiento…

–Es verdad –dijo Sal con alegría.

–Pero Mati –intervino Ven –Cuando sean 20 tiradas, nos va a salir un diagrama, ¡enorme!

–Tienes razón, pero no hace falta hacer el diagrama –aceptó Mati –Se trata de calcular la probabilidad de una intersección de sucesos independientes, porque el resultado de cada lanzamiento es independiente del anterior. Un suceso es que la primera salga cara, otro que la segunda salga cara, el tercero que salga cara en la tercera y el cuarto, que la cuarta tirada dé cara. Cada uno de estos sucesos, tiene probabilidad 1/2, como hemos dicho, ¿verdad? Eso significa que en cada tirada de las 4, la probabilidad de que salga cara es 1/2 o sea, de un 50%.

–Ahora bien, la probabilidad de que las cuatro veces nos salga cara es la probabilidad de la intersección, y eso se calcula sabiendo que, como son independientes, la probabilidad de la intersección es igual al producto de las probabilidades.

–¿Ves, Mati? –dijo Ven con vehemencia –Es casi imposible que pase, y ha pasado

–Tú lo has dicho, Ven –dijo ella –casi imposible, pero no imposible.

–¡Que mi moneda es buena, de verdad! –se quejó Sal.

–A ver, Ven –dijo la pelirroja –Si hacemos otra vez el sorteo, ¿tú que pedirías, cara o cruz?

El pequeño se quedó un rato pensando, al cabo del cual contestó:

—Cruz.

–¿¿Cruz?? –preguntó Sal sorprendido –¿No decías que en mi moneda sólo sale cara?

–Ya… -dijo Ven mirando al suelo –Pero en realidad, creo que tu moneda es auténtica y como ya han salido 4 caras… toca cruz.

–Huy, creo que Ven ha caído en la falacia del jugador… –dijo Mati con voz misteriosa.

–¿La qué? –preguntó Sal con los ojos de par en par.

–Una falacia es una mentira o engaño –empezó a explicarles –La falacia del jugador, o falacia de Montecarlo, es la falsa creencia de que lo sucedido anteriormente en un experimento aleatorio, al azar, afectará al resultado de los experimentos siguientes.

–No entiendo nada de nada… –confesó Ven.

–Es lo que tú acabas de hacer, Ven –continuó ella –Crees que el hecho de que hayan salido ya 4 veces caras, afectará al 5º lanzamiento y no es verdad. La probabilidad de obtener cruz en el 5º lanzamiento es, de nuevo, 1/2, como siempre.

–Claro… Qué tontería…

–Bueno, Ven, esa tontería como tú la llamas, engaña a mucha gente que piensa que si sale varias 4 veces seguida cara, lo lógico es apostar a cruz por que ya toca. Y no, están confundiendo la probabilidad de obtener 5 caras seguidas con la probabilidad de obtener cara en el 5º lanzamiento.

–¡Toma, toma, toma! ¡Es verdad! –el pequeño estaba alucinando.

–Cuando lo lógico sería lo contrario –siguió la pelirroja.

–¿Lo contrario? ¿Por qué, Mati? Si cara y cruz tienen la misma probabilidad –el gafotas estaba muy intrigado.

–Ya, pero si sale muchas veces seguida cara –siguió ésta –lo que parece indicar es que la monedad no está bien compensada y que, por lo tanto, tiene más probabilidad de salir cara.

–Cierto… -se quedó pensando Sal –Si la moneda es buena, no importa lo que ha pasado antes.

–Eso es, Sal, en ese caso decimos que son experimentos independientes –confirmó la gafotas –El resultado de un experimento no depende del anterior.

–¿Y hay experimento dependientes? –preguntó Sal de nuevo.

–Sí, naturalmente –dijo Mati –Por ejemplo, si tenemos 5 bolas rojas y 3 bolas verdes en una bolsa, ¿cuál es la probabilidad de meter la mano y sin mirar sacar una bola roja?

Los niños se quedaron pensando.

–5/8 –dijo Sal

–Muy bien –sonrió Mati — La dejamos fuera ¿Y la probabilidad de que la segunda sea roja?

Sal y Ven montaron de nuevo su gabinete de resolución de problemas.

–Un momento, Mati –preguntó el pequeño –La primera que sacamos fue roja, ¿no?

–Me alegro de que me hagas esa pregunta –respondió Mati haciéndose la interesante –Eso significa que el resultado del segundo experimento depende del primero, ¿no? Son experimentos dependientes.

–¡Claro! –la carita de Sal brillaba con alegría –¿Cómo se calcula entonces, Mati?

–Vamos a verlo en el cuaderno –propuso Mati –Lo que queremos conocer es la probabilidad de que en la segunda extracción (ya hay una bola fuera) saquemos una bola roja. A esa probabilidad que queremos calcular la llamaremos P(2ªR). Para calcular P(2ªR) vamos a necesitar calcular otras probabilidades antes. Por ejemplo, la probabilidad de que la 2ª bola sea roja condicionada al hecho de que la primera que salió fuese roja, lo llamamos P(2ªR | 1ªR)

–De la misma manera, necesitaremos conocer la probabilidad de que la segunda bola sea roja condicionada al hecho contrario, es decir, al hecho de que la primera no fuese roja.

–Por último, necesitaremos usar la probabilidad de que la 1ª bola extraída fuese roja y la del suceso contrario, la de que la 1ª bola no fuese roja.

–Con todo esto, ya podemos calcular la probabilidad de que la segunda vez, extraigamos una bola roja, o sea, P(2ªR), usando esta fórmula

–Ya sólo –dijo Mati –necesitamos calcular esos 4 términos para conseguir lo que queremos ¿Me ayudáis?

–¡Sí! –dijeron los niños al unísono.

–Empezamos por la probabilidad de que la 2ª bola sea roja sabiendo que ya sacamos una y que fue roja –les dijo.

–A ver… –comenzó hablando Sal –casos posibles son 7 porque ya hay una bola menos…y casos favorables, serán 4 porque había 5 bolas rojas pero ya sacamos 1.

–¡Muy bien! ..les animó Mati –Ahora la otra condicionada, la probabilidad de que la segunda sea roja sabiendo que la primera que sacamos no lo era.

–Me toca –dijo Ven animado –Caso posibles son 7, claro, y casos favorables… 5, las 5 bolas rojas.

–Pero bueno…-Mati sonreía orgullosa –Lo que queda ya lo tenéis muy fácil

Los niños terminaron de calcular los términos que le faltaban

–¡Perfecto! –dijo la pelirroja –Ya lo tenemos todo

–¡Toma, toma, toma! –el pequeño Ven estaba alucinando.

–Me encanta, Mati –añadió el gafotas.

–Me alegro –dijo ella –El cálculo de probabilidades es muy entretenido y sencillo. Con esto y con un poco de observación, una familia española, los Pelayo, ganaron mucho dinero. Pero a vosotros todavía no os interesa el dinero, ¿verdad?

–No, ¡nos interesa el fútbol! –dijo Ven.

–Bueno, y las matemáticas –añadió Sal con una sonrisa.

—Volviendo al asunto del fútbol –empezó a decir Mati –si queréis, por ejemplo, elegir campo en el fútbol y no estáis seguros de que la moneda esté equilibrada, os enseñaré a hacer un sorteo justo.

—¿Cómo? —preguntó casi gritando Sal sonriendo esperando la respuesta de Mati.

—Muy fácil, haciendo el sorteo a dos tiradas –propuso ella –La moneda será lanzada dos veces, y los jugadores elegirán sólo entre dos posibilidades: (cara, cruz) y (cruz,cara). Si las dos veces la moneda saca lo mismo, es decir (cara, cara) o (cruz, cruz), repetimos los dos lanzamientos. Pero los dos sucesos (cara, cruz) y (cruz, cara) tienen la misma probabilidad de salir. Nadie puede enfadarse.

–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven –Vamos, Gauss, vamos a repetir el sorteo… ¿Dónde está Gauss?

–Creo que se quedó frito escuchando la explicación…

Tags: probabilidad, probabilidad condicionada | Almacenado en: La hora de las tareas
3 comentarios

No todo es lo que parece

11 de junio de 2012

Nada es verdad, ni mentira dicen algunos, y terminan la frase atribuyendo la causa de la posible diferencia en el punto de vista al color del cristal con que se mira. Puede ser… En este sentido siempre he sido más de Descartes y su Discurso del Método:

no admitir como verdadera cosa alguna, como no supiese con evidencia que lo es; es decir, evitar cuidadosamente la precipitación y la prevención, y no comprender en mis juicios nada más que lo que se presentase tan clara y distintamente a mí espíritu, que no hubiese ninguna ocasión de ponerlo en duda.

No, no estoy hablando de rescates, no tengo ganas de entrar en debates nominalistas, yo tampoco.

Imaginen que quieren construir unos depósitos de combustible cilíndricos de gran capacidad, por ejemplo para un transbordador espacial. Imaginen que para ello lo construyen en varias trozos cilíndricos que luego encajarán unos con otros, formando el depósito cilíndrico final.

Parece evidente que es importante que las distintas partes encajen bien entre sí, es decir, que la base de dichos cilindros midan todas lo mismo, y sobre todo, que sean círculos perfectos. Digo yo que una fuga de combustible puede resultar, cuanto menos, inapropiada ¿Cómo comprobar esto último? Es decir, ¿cómo comprobamos que la base del cilindro es un círculo perfecto?

Uno podría pensar que si mide un número alto de diámetros distintos de la base y todos miden lo mismo, eso tiene que ser un círculo, ¿no?

¿Cuántos diámetros medimos? Yo que sé… 100.000 millones por ejemplo. Si, total, hay infinitos diámetros en un círculo… ¿Podemos estar seguros de que si los 100.000 millones de diámetros miden lo mismo lo que estamos midiendo es un círculo?

Si en lugar de depósitos gigantescos de combustible medimos tubos, ¿nos servirá un calibrador de fontanero para saber si efectivamente el tubo es perfectamente circular? Si lo abrimos con una apertura concreta y lo hacemos girar alrededor de nuestro tubo, eso tiene que ser redondo, ¿no? ¿Sí?

Si respondemos afirmativamente a las dos preguntas finales de los dos parrafos anteriores es porque estamos asumiendo que una figura geométrica con la propiedad de ser igual de ancha en todas las direcciones es un círculo ¿Sí?

En geometría, se llama anchura de un conjunto en el plano a la menor distancia entre 2 rectas paralelas que lo encierran, es decir, la anchura de un objeto es la del pasillo más estrecho en el que cabe. Con esta definición, lo que estaríamos afirmando respondiendo sí a las preguntas anteriormente mencionadas es que un conjunto que tenga anchura constante, la misma en todas las direcciones, es un círculo ¿Sí?

Vamos ver qué pasa con otras figuras planas conocidas. Un triángulo por ejemplo, tiene ¿anchura constante?

Pues como se ve en la figura anterior, si calibramos por el lado del triángulo la medida es mayor que si calibramos desde uno de los lados al vértice opuesto. No nos sirve…

¿Y un cuadrado? ¿Tiene anchura constante?

Vaya, pues parece que tampoco. Porque en el cuadrado de la figura, un cuadrado de lado 1, si lo calibramos de lado a lado medirá exatcamente eso, 1, y si lo calibramos según una diagonal 8en rojo en la figura) medirá

√2.

¿Y un hexágono? ¿Será una figura de anchura constante? No sé, parece más redondito…

Tampoco, como se aprecia en la figura de la derecha. si calibramos en la dirección perpendicular a la línea verde, la medida es mayor que cuando calibramos en perpendicular a la línea de color naranja.

Esto puede inducir a pensar que efectivamente, como habíamos sospechado, la única figura geométrica plana que tiene anchura constante es un círculo, ¿verdad?

Pues no. Existen otras figuras, infinitas de hecho, que tienen anchura constante y que no son círculos. Lo cual puede ser un poco chungo en el caso de las piezas del depósito de combustible de un transbordador espacial. Estas posibles pequeñas imperfecciones en el encaje se resuelven usando juntas tóricas (con forma de flotador) de goma que lo amortigüen. Ahora, eso sí, hay que asegurarse de que estas juntas estén fabricadas con un material adecuado y que, por ejemplo, no sean demasiado sensibles a los cambios de temperaturas y esas cosas, no sea que nos pase como pasó con el Challenger*… y eso no está bonito.

Efectivamente, una de las figuras de anchura constante más conocidas son los polígonos de Reuleaux, que reciben este nombre en honor del ingeniero alemán que los desarrolló, Franz Reuleaux. Vamos a fijarnos por ejemplo en el más simple de estos polígonos de anchura constante, el triángulo de Reuleaux.

Efectivamente, este tipo de triángulos tiene anchura constante. Si lo medimos con el calibrador, en cualquier dirección obtenemos el mismo resultado. Y, evidentemente no son círculos

¿Cómo se dibuja un triángulo de Reuleaux?

Basta comenzar con un triángulo equilátero. Ahora, con un compás, nos apoyamos en cada uno de los 3 vértices de dicho triángulo, y trazamos el arco de circunferencia que une los otros dos vértices.

¿Qué interés, aparte de ser de anchura constante, puede tener un polígono de Reuleaux en general, o un triángulo de éstos en particular?

Por ejemplo, para el diseño de tapas de alcantarilla. Ya, ya sé que con hacerlas circulares se resuelve el problema, pero nunca hay que renunciar a mejorar un poco los pequeños detalles de la vida con el fin de hacerlo más bonito o, al menos diferente. Si diseñamos una tapa de alcantarilla con esta forma, como cualquier posición tiene el mismo ancho, la tapa así diseñada nunca se caería hacia dentro, no habría forma de meterla. Mientras que si, por ejemplo la tapa fuese cuadrada, bastaría con levantarla, y colarla derechita, usando la diagonal del hueco que es siempre mayor que el lado del cuadrado.

Además de tapas de alcantarillas, los triángulos de Reuleaux se han usado para el diseño de una taladradora que hace agujeros casi cuadrados. Como se ve en la animación de la izquierda, en las esquinas que da un poco de área sin recubrir por lo que el resultado es un cuadrado con las esquienas redondeadas. El diseño de este taladro inspirado en los triángulos de Reuleaux lleva la firma de Harry James Watts que lo inventó en 1914.

También en el diseño de motores de coches se han usado los triángulos de Reuleaux. Bueno, casi se han usado… Porque en realidad, los triángulos que se usan en el diseño de los rotores del motor Wankel, tienen los lados un poco más aplanados que los triángulos de Reuleaux y, por tanto, no tienen anchura constante. La ventaja de usar este tipo de rotores en lugar de los pistones habituales, permiten que el motor Wankel sea más silencioso, suave y fiable.

Pero no queda ahí la cosa, no, porque como dijo aquel torero, hay gente pa tó… Aunque ya había podido comprobar que una bicicleta, ésta de era de juguete, podía rodar suavemente si sus ruedas eran triángulos de Reuleaux, de hecho nos regalaron una a cada uno de los participantes en el Kyoto CGGT 2007 (celebrado en honor de Jin Akiyama and Vašek Chvátal),

poco después. Guan Baihua en 2009, diseñó una bicicleta donde la rueda de delante era un pentágono de Reuleaux y la de detrás un triángulo del mismo.

Como cuestión estética, los polígonos de Reuleaux aparecen en el diseño de monedas, en la arquitectura…

Lo dejamos por aquí y os invito a que busquéis más apariciones de los polígonos de Reuleaux. Sólo un par de cosas más. La primera es que como dije casi al principio de esta entrada, hay infinitas figuras que tienen anchura constante y es cierto. En este enlace se explica detalladamente una forma de generarlas.

*Y la segunda, tiene que ver con la referencia al accidente del transbordador espacial Challenger en enero de 1986. Algunos de nosotros ya habíamos nacido… Tras el dramático accidente se creó, como se hace en estos casos, una comisión que investigara las causa del mismo. En esta ocasión, fue la comisión conocida como la comisión Rogers. Casualmente, ¿eh?, he dicho casualmente, en la citada comisión todos los integrantes, menos uno, eran personas bastante vinculadas a la NASA, al ejército o al gobierno de los Estados Unidos. Todos menos uno. Pero ese uno era nada más y nada menos que Richard Feynman, entre otras cosas, Premio Nobel de Física en 1965. Supongo que el nombre de Feynmann le daba mucho más prestigio a los resultados de la investigación, y aunque éste no era conocido especialmente por su carácter dócil y reservado, tenía ya 68 años y había tenido que soportar una importante cirugía para escapar de un cáncer. Podría parecer que no se iba a implicar demasiado en este asunto. Podría parecer… Pero si alguien lo llegó a pensar, se equivocó. Feynmann no sólo se implicó sino que se atrevió a dar una versión diferente a la oficial de la Comisión sobre las causas del accidente. Y lo hizo en televisión, durante una rueda de prensa. Para probar que el problema había estado en el material utilizado para las juntas tóricas, introdujo un trozo de este material en un vaso de agua con hielo. La elasticidad de las mismas y su estanqueidad no soportaban las bajas temperaturas y aquella mañana de 1986 hacía demasiado frío en Florida. En el libro ¿Qué te importa lo que piensen los demás?, aparte de las anécdotas divertidísimas de este genio que también tocaba los bongos, se puede leer más sobre su trabajo en la Comisión.

Tags: Anchura, anchura constante, Challenger, Motor Wankel, Polígonos de Reuleaux, Richard Feynmann, Triángulos de Reuleaux | Almacenado en: Ahora que los niños salieron a jugar...
24 comentarios

No te muevas tanto…

06 de junio de 2012

–Mira a Gauss, Sal ¡Se parece a un conejo de Fibonacci!

–¡Hala, es verdad! Y mira mis piernas, parecen de goma…

–Y mi brazo… –siguió el pequeño entusiasmado –Mira, ¡ese niño está loco! Yo levanto el brazo izquierdo y él ¡levanta el derecho!

–Claro, Ven –respondió su hermano –Es un espejo.

–¿Y? ¿Por qué me veo al revés? ¿Por qué no me veo la cabeza abajo y los pies arriba?

–Pues porque el plano de simetría es el espejo, que es perpendicular al suelo – intervino Mati.

–¿¿Qué?? –los niños se quedaron mirando a Mati perplejos. Gauss cambió de espejo, su identidad de conejo no le convencía ni mucho ni poco.

–Tranquilos, chicos. Voy a tratar de explicarlo –dijo la pelirroja con una sonrisa –Os contaré que es una simetría. Pero empezaremos por el plano, ¿vale?

–¿Qué plano, Mati? –preguntó Sal intrigado.

–En el de la hoja de nuestro cuaderno, ¿os apetece?

–Sí, claro –respondió Sal.

–Como si viajáramos hasta Planilandia –añadió Mati.

–¿Dónde está Planilandia? –preguntó inmediantamente Ven –¿Es un parque de atracciones?

–No, Planilandia es un país dónde todo ocurre como en una inmensa hoja de papel –siguió la gafotas –Otro día hablaremos de ese libro de Edwin Abbott. Hoy os voy a tratar de explicar cómo funcionarían los espejos de este país en una hoja de papel, lo que los matemáticos llamamos simetrías en el plano.

–¡Vale! –dijo Ven con entusiasmo mientras Sal se ajustaba las gafitas sobre la nariz.

–Imaginaos que tenemos un Gauss en nuestro país plano frente a un espejo, que en nuestro plano es sólo una recta. Vamos a dibujar al Gauss que se refleja, al simétrico de Gauss respecto de esa recta.

–¡Mola! –gritó Ven mientras su mascota miraba de reojo al cuaderno de Mati.

–Antes de reflejar a Gauss, vamos a hacerlo con un triángulo que es más sencillo, ¿os parece? –propuso Mati.

–Venga –respondió el gafotas.

–Calculamos primero el punto simétrico de A –empezó a decir Mati –Después calcularemos el de B y el de C y podremos dibujar el triángulo simétrico.

–¿Cómo hacemos el simétrico de A, Mati? ¿Lo podemos pintar nosotros? –preguntó Sal.

–Claro. Trazamos desde A una recta perpendicular a la nuestra, la que representa el espejo, que llamamos eje de simetría…

–¿Perpendicular es que forme ángulo recto como la esquina de una portería? –preguntó el pequeño.

–Eso es, Ven –continuó Mati –Llamaremos M al punto de corte de esta nueva recta con el eje de simetría.

–Ese punto, M, estará a la misma distancia de A que de su punto simétrico, que llamaremos A*, justo en la mitad, ¿sí?

–Sí… –dijo Sal muy concentrado.

–Pues el simétrico de A, A*, es un punto que está sobre la recta que acabamos de dibujar, a la misma distancia de M que el punto A. Medimos la distancia de A hasta M…

–¡6 cuadritos!

–Muy bien, Ven. Ahora contamos 6 cuadritos hacia la derecha sobre la recta, empezando en M… y aquí tenemos al simétrico de A, le ponemos su nombre… A*…

–¿Me dejas hacer a mí el simétrico de B, Mati? Pero solo –preguntó Sal.

–No, y yo también, oye… –protestó el pequeño.

–Claro, entre los dos, Ven –contestó su hermano, mientras Gauss retorcía un poco el hocico y se hacía el indiferente ante la posibilidad de calcular el simétrico de un punto respecto a una recta, “como si me importara mucho…” pensó con un poco de pelusilla.

–Pintamos la recta perpendicular… -mascullaba Ven –Aquí está el punto del medio… ¿le llamamos también M, Mati?

–Puedes llamarlo N, si te apetece –contestó la pelirroja con un guiño.

– 9 cuadritos desde B hasta N… –contaba el gafotas –Ahora 9 cuadritos a partir de N, y ahí está B*.

–¡Te pillamos, so simétrico de B! –dijo Ven mientras apuntaba a la libreta con el índice y el pulgar a modo de pistola.

–Ahora el de C, ¿cómo llamamos al punto de en medio, Ven?

–Llámalo P, forastero… –contestó Ven con tono de vaquero, que este niño es muy novelero y se mete rápido en el papel…

Los dos hermanos dibujaron el simétrico de C en el papel, mientras Gauss se miraba la pata derecha como si nada de aquello fuera con él.

–Ya, ya tenéis los simétricos de los 3 puntos –intervino Mati –ya podéis pintar el triángulo simétrico.

–¡Ahora con Gauss! –dijo Sal y su mascota salió de su ensimismamiento con alegría para descubrir que los niños seguían absortos en el cuaderno.

–Muy bien, chicos – intervino Mati -Aunque hemos hecho un poco de trampa…

–¿Trampa? ¿Por qué? –Ven frunció el ceño.

–Porque en Planilandia no se puede hacer ese movimiento…

–¿Por qué? –preguntó Sal intrigado.

–Porque cuando hacemos una simetría, es como si levantásemos a Gauss y le diéramos la vuelta en el aire…

–¿¿Y?? –Ven estaba cada vez más intrigado.

–Que en Planilandia nadie puede salir de la hoja de papel –concluyó Mati –No hay forma de conseguir el simétrico de Gauss con un movimiento dentro del propio plano, del propio papel.

–Claaaaaaro… –Sal sonreía –Es cierto…

–Por esa razón –continuó la gafotas –los matemáticos llamamos a la simetría, movimiento inverso. Hay que salirse del plano y darle la vuelta la figura de Gauss para que coincida con la otra.

–¡Toma, toma, toma! ¡Es verdad! Gauss no se podrá mover en Planilandia –la cara de Ven se entristeció –Pobre…

–Claro que se podrá mover –corrigió Mati –Pero usando movimientos directos, por ejemplo, una traslación o un giro.

–¿Qué es una traslación? –preguntó el gafotas.

–Una traslación consiste en mover el objeto usando un vector, el vector de la traslación.

–¿Y cómo se hace? –preguntó Sal.

–Decidme las coordenadas de un vector…

—(7,9) –dijo Ven –Nuestras edades.

–Vamos a hacer una traslación de vector (7,9) a Gauss –propuso Mati –Tenemos que mover cada punto según esa dirección, 7 cuadritos a la derecha y 9 hacia arriba…

–Cuando hayamos movido un punto, llevamos sobre él el resto de la silueta de Gauss y ya está –concluyó ella.

–¡Y sin salirse de Planilandia! –dijo Ven abrazando a su mascota –Sólo hay que arrastrarlo.

–Efectivamente, la traslación es un movimiento directo porque no nos salimos del plano –les contó Mati.

–¿Y el giro? ¿Cómo es el giro? –Sal estaba entregado a los movimientos del plano. Gauss se estaba mosqueando un poco…

–Para identificar un giro, necesitamos elegir un punto, centro del giro, y un ángulo, el ángulo de giro –les contó su amiga –¿qué punto queréis que sea el centro del giro?

–¿Tiene que ser un punto sobre el dibujo de Gauss? –preguntó Sal.

–Como queráis –contestó la pelirroja –Pero no es necesario.

–Venga, éste –dijo el pequeño pintando un punto azul sobre el papel.

Gauss gruñó, pero de mentirijilla, en el fondo tanto protagonismo le estaba gustando…

–Estupendo –afirmó Mati –Y lo giramos 45 grados, la mitad de un ángulo recto, ¿vale?

–¡Vale! –dijeron los chicos al unísono.

–Para ello, trazamos una línea desde el centro de giro hasta la punta de la cola de Gauss y giramos era línea 45 grados, apoyados en el centro y vemos hasta donde llega Gauss, como si la punta de su cola estuviese pegada a la línea.

–¡Toma, toma, toma! ¡Qué gracioso! –Ven volvió a abrazar a su mascota.

–¿Veis? Estos 2 movimientos, el giro y la traslación, son movimientos directos –dijo Mati –Se pueden hacer sin salirse del plano.

–Me gusta mucho esto, Mati…

–A mí también, Sal –contestó ella –Y se pueden usar para enlosar el plano con baldosas de diferentes formas, según como movamos las losetas… Pero eso ya lo vemos otro día, ahora volvamos a casa, que es hora de merendar.

–¡Sí, sí! –insistió el pequeño –Tanto movimiento me ha dado mucha hambre…

Tags: Giro, Movimientos directos, Movimientos en el plano, Movimientos inversos, Simetría, Traslación | Almacenado en: La hora de las tareas
Comentarios desactivados en No te muevas tanto…

¿A quién rescatamos el último?

04 de junio de 2012

En estos días compruebo, sin alegría, que la palabra rescate ha perdido el cariz romántico. Ése que de pequeña olía a príncipe soso cabalgando sobre un caballo (no sé por qué blanco) con una capa al viento y que unos años más tarde se transformaba en un arqueólogo tocado con un sombrero Fedora y un látigo en la mano. Y sé que no soy la única, lamentablemente. Estoy segura de que cada uno de nosotros tiene en sus recuerdos de sueños infantiles o púberes rescatadores y/o rescatadoras muy diferentes… Eso sí, casi seguro que ninguno de nosotros soñó con que lo rescataba aquella chica que nacía en Hamburgo un día de julio de 1954…

Pero hoy es lunes y los niños han salido a jugar, las noticias ya nos saturan de problemas que no sabemos resolver, o que, al menos no se están resolviendo, así que dejemos a los profesionales que nos informen sobre ellos y vamos a plantear un problema que nos sirva para pensar un rato y que poder compartir a la hora del café o del aperitivo con nuestros amigos, por si estamos cansados de hablar de cómo está la cosa.

El pasado viernes tuve la suerte de poder asistir a la conferencia Magia y Matemáticas que el Dr. Carlos Vinuesa impartió en la Facultad de Matemáticas de la Universidad de Sevilla. Aparte de la indiscutible capacidad de Carlos para atraer y sorprender con sus juegos de magia, los asistentes a la misma pudimos entrar entre bambalinas y descubrir qué Matemáticas se escondían detrás de aquella magia. No, no voy a contar los secretos de Vinuesa, os invito a que lo vayáis a a ver si tenéis ocasión.

Pero si os voy a contar un problema que él nos recordó en su conferencia y que es conocido como el Problema de Flavio Josefo. En su obra La guerra de los judíos, obra que algunos ponen un poco en tela de juicio en cuanto a su rigor y neutralidad, puesto que fue escrita después de que Josefo fuera capturado por los romanos y se le nota un pelín filorromana, este historiador judío cuenta como él y 40 soldados judíos quedaron atrapados en una cueva, rodeados de romanos, y que prefiririeron suicidarse antes que entregarse a los romanos. Si, hay gente pa tó. Pero como estaban así, en plan festivo, decidieron ir ejecutando a las víctimas de una forma original, no hay que perder el buen humor en ninguna situación: ¡que no se diga! Hay varias versiones sobre el método elegido para el macabro sorteo, pero la más extendida es la siguiente:

Se colocan todos los soldados en un círculo, el primero se salva, matamos al segundo, saltamos uno, matamos al cuarto, saltamos uno, matamos al siguiente, saltamos uno… y así sucesivamente hasta que queda el último que se matará sólo.

Si tenemos 12 soldados alrededor del círculo, en la primera vuelta, mataríamos a los que aparecen en amarillo en la siguiente figura

Al llegar al 12, que en paz descanse, nos saltaríamos al 1 de nuevo (ya se ha escapado 2 veces) e iríamos a por el 3. Vamos que al final de la segunda vuelta, habrían caído los que aparecen en verde en la siguiente figura

Pues bien, de nuevo tras despedirnos del 11, volvemos a saltar el 1, le damos boleto al 5, nos saltamos al 9 y nos queda…

Por lo tanto, el último que queda tras esta estrategia graciosa es el 9.

Nota mental: si somos 12 en la rueda, colocarme en la posición número 9.

Según la historia de Flavio Josefo aquel día en la cueva, al final sólo quedaron él y un amigo, que decidieron entregarse a los romanos antes que suicidarse. Dicen que él atribuyó su salvación a la Providencia. No me voy a meter en esto, pero a lo mejor es que Flavio y su colega habían hecho bien las cuentas…

¿Qué cuentas son las que hay que hacer para ser el último y decidir si suicidarte o echarte unas risas con los romanos?

Bueno, ya hemos visto que si son 12 en la rueda, la posición que más mola es la 9. Vamos a estudiar otros casos, a ver si inferimos algún método…

Si sólo somos 4 jugadores el último en morir sería el que estuviese en la posición 1…

Si hay 5 jugadores en círculo, el que se salva es el de la posición 3…

Cuando hay 6 en el círculo, se salva el 5…

La 7 es la posición buena cuando son 7…

Otra vez la posición 1, si son 8… Vamos a recoger todos estos datos en una tabla a ver si nos sugieren alguna regla…

Si nos fijamos en la tabla anterior, que para eso también lo hemos coloreado en amarillo canario, la posición 1 es la última en ser elegida en todas las ruedas cuyo número de jugadores es una potencia de 2 (1, 2, 4, 8, 16…) Luego, entre cada dos potencias de 2, lo que aparece es la sucesión de los impares, comenzando con el 3 justo después de dicha potencia de 2.

¿Se cumple siempre? Pues sí, se cumplirá siempre, otro día os contaré la demostración. Hoy nos quedamos sólo con el truco, aunque preferiría que lo usarais para otra cosa que no sea una ronda de suicidios a la salud de algún imperio. Es más gracioso, por ejemplo, para elegir quién paga una ronda en un bar, que lo pague el último en salvarse.

Para comprobar si lo he explicado con claridad, vamos a poner otro ejemplo. Supongamos que tenemos 27 países que forman una posible comunidad y que empiezan a sobrar algunos. Supongamos que aplicamos el método del problema del Josefo para ir eliminando uno a uno a estos países, ¿en qué posición hay que colocarse para ser el último en salir de esta comunidad? Vamos a hacer las cuentas. Buscamos la potencia de 2 más próxima a 27 pero inferior a él. Como 27 está entre 16 y 32, la potencia buscada es 16, 2 elevado a 4. Ahora, si queréis en una tablita, rellenáis con impares hasta llegar al 27…

Pues sí, para ser el último en salir hay que colocarse en la posición 23 en la rueda, que viene a caer un poco al sur del mar Báltico, un poco a la izquierda de Polonia y sin llegar a Francia…

Tags: Flavio Josefo, Magia y Matemáticas | Almacenado en: Ahora que los niños salieron a jugar...
1 comentario »

Seguimos pendientes de las rectas…

30 de mayo de 2012

Anteriormente en Mati, una profesora muy particular…

–¡Toma, toma, toma! ¡CÓMO MOLA! –a Ven se le salían los ojos de las órbitas.

–¡Me encanta, Mati! –Sal estaba también entusiasmado.

–Pues aún hay más…–respondió ella con tono de misterio –pero ésas la dejaremos pendientes… Ahora vamos a dar un paseo por la playa

En el capítulo de hoy…

–Mira, Sal, el tobogán, ¿nos tiramos? –preguntó Ven animado –Parece muy emocionante, mira cuánta pendiente tiene…

–No, no tiene tanta pendiente, Ven, es casi como el del parque de nuestra casa. No seas exagerado…

–Que no, Sal, que este tiene más pendiente –insistió el pequeño.

–¿Cómo lo puedes saber? –preguntó su hermano mirando por encima de sus gafotas.

–Espera, que me tiro y te lo digo –dijo Ven y salió corriendo al tobogán.

Mati, Sal y Gauss se quedaron esperando la opinión del experto que volvió en pocos minutos sonriente.

–Me he quemado el culete, estaba muy caliente –dijo éste –Pero tiene la misma pendiente, he sentido las mismas cosquillitas en la barriga.

–Bueno, bueno –intervino la pelirroja sonriendo –Es una escala de medida bastante original, pero si queréis os cuento cómo se puede medir exactamente una pendiente.

–¡Sí, Mati! –dijeron los dos hermanos a la vez, Gauss se tumbó panza arriba para tomar el sol.

–La pendiente del tobogán, es la pendiente de la recta que lo representa –comenzó a hablar Mati.

–¡Toma, rectas! ¡Mola! –interrumpió Ven.

–Sí, para eso también sirve conocer las rectas –dijo Mati y continuó guiñando un ojo–Ya veis que son muy interesantes… Pues bien, vamos a usar para explicarlo una recta y lo hacemos con un dibujo, ¿vale?

Mati sacó su cuaderno y dibujó una recta que pasaba por los puntos A y B de coordenadas (1,1) y (4,3), respectivamente.

–Ésta es la recta de antes, ¿verdad, Mati? –preguntó Sal.

–¡Ajá! Voy a usar la misma porque vamos a ver nuevas ecuaciones de la recta –dijo Mati –Cuando queremos calcular la pendiente de una recta, lo que estamos tratando de medir es el ángulo que forma con el suelo, como cuando medimos la pendiente del tobogán. Nuestro suelo es el eje de las x, donde medimos la primera coordenada.

–Pero fijaos que este ángulo, esta elevación es la misma que si el suelo estuviese a la altura del punto A –continuó la gafotas.

–¡Toma, toma, toma! ¡Claro! –gritó Ven sobresaltando a Gauss en su baño solar.

–¿Cómo medimos el ángulo, Mati? –preguntó Sal.

–En realidad, cuando hablamos de la pendiente de una recta no medimos el ángulo como tal, sino una cantidad propia del ángulo, que es la tangente de dicho ángulo –respondió ella.

–¿Qué es la tangente? –quiso saber Sal.

–Bueno, es una característica que nos permite identificar a un ángulo sin saber cuánto mide –comenzó a decir Mati –pero nos ayuda a determinar su inclinación. Para ello, vamos a medir la distancia en vertical entre los dos puntos A y B, y la distancia en horizontal entre los 2. Fijaos, tenemos un triángulo rectángulo, como en el Teorema de Pitágoras, ¿os acordáis? –les preguntó la pelirroja.

–¡¡Sí, sí!! ¡¡Con los catetos!!

–Eso es, Ven. Pues la tangente del ángulo que queremos se calcula dividiendo entre sí la longitud de los catetos –continuó Mati –Dividimos el cateto que no toca al ángulo por el cateto que si la toca.

–Que en nuestro caso particular sería…

–Pero, Mati –dijo Sal pensativo –Los catetos miden lo mismo que las coordenadas del vector AB, ¿no?

–Efectivamente, cielo –Mati se sorprendió alegremente –Si conocemos el vector de la recta, la pendiente de ésta se calcula dividiendo la segunda coordenada del vector por la primera coordenada del mismo. Nos ha salido positiva porque el ángulo que forma es menor que 90º, agudo. Eso significa que la recta va subiendo cuando nos movemos hacia la derecha. –siguió Mati –Pero cuando el ángulo es obtuso, mayor de 90º, la pendiente será negativa y la recta irá bajando cuando nos movemos la derecha también.

–¡Toma, toma, toma! ¡La del tobogán es negativa porque cuando vamos hacia adelante, el tobogán va bajando!–como siempre Ven estaba estusiasmado.

–¡Exacto! Pues aún hay más –siguió nuestra amiga matemática –Conociendo un punto de la recta, por ejemplo A y la pendiente, m, podemos calcular otra ecuación de la recta: la ecuación punto-pendiente.

–¡Hala, qué suertudas las rectas! –dijo Ven –Tiene un montón de ecuaciones…

–Pues no se vayan todavía, aún hay más –dijo cómicamente Mati –Vamos a dejar sola a la y en el miembro de la derecha…

–¡Otra! –dijo Sal con sorpresa.

–A esta nueva ecuación de la recta, en la que se expresa el valor de la coordenada y de un punto en función de x, se le llama ecuación explícita de la recta.

–Ésa ya la vimos, ¿no, Mati? –preguntó Ven.

–No, no. La que vimos fue la ecuación implícita. Pero ya veréis, hacemos lo mismo con la ecuación implícta de la recta, es decir, dejamos a la y sola en el primer miembro… –Mati continuó con voz de misterio.

–¡Toma! ¡Sale lo mismo! –se asombró el pequeño.

–Claro, pero aún hay más… –continuó Mati –¿Qué número multiplica a la x?

–¡2/3! -dijo Sal –¡La pendiente!

–¡Eso es! –corroboró ella — Por lo tanto, podíamos conocer la pendiente simplemente despejando la y en la ecuación implícita y saber si la recta se inclina hacia arriba o hacia abajo. Si tenemos la ecuación explícita de una recta, la pendiente de la misma es el número que multiplica a la x, es decir, el coeficiente de x en la ecuación explícita.

–Pues a nuestra mascota… –dijo Ven mirando a Gauss todo despatarrado en la arena –No le va lo de las pendientes, prefiere estar tumbado…

Tags: coordenadas, coordenadas cartesianas, ecuación de primer grado, ecuación lineal, ecuaciones de la recta | Almacenado en: La hora de las tareas
2 comentarios

Un niño grande que juega con papel

28 de mayo de 2012

Cuando dices que eres investigadora en el área de Matemáticas no es difícil que alguien te pregunte ¿aún quedan cosas por descubrir en Matemáticas? ¿No está todo descubierto? Es entonces cuando tratas de explicar, sin palabros, que efectivamente no, no está todo descubierto y que, aparte de los problemas matemáticos clásicos planteados por ilustres matemáticos y que aún siguen sin resolver desafiando a las mentes que se dedican a ello, el desarrollo de la informática y las nuevas tecnologías hace imprescindible el avance de esta disciplina en la resolución de nuevos problemas, problemas sobre todo de tipo computacional. En ese sentido, por ejemplo, entre otras áreas, se encuentra la Geometría Computacional. Es ahora cuando me toca explicar qué es la Geometría Computacional, y aunque traté en su tiempo de hacerlo en esta entrada que publiqué en Gaussianos, tras una invitación del editor del mismo y he tratado de convencer de la belleza y versatilidad de sus estudios en dos entradas de Amazings.es, una primera explicando las aplicaciones del Diagrama de Voronoi y en la segunda parte, mostrando algunas estrategias de la materia para resolver el problema del cálculo del Diagrama de Voronoi, en pocas palabras, se podría decir que la Geometría Computacional se ocupa de tratar de resolver problemas de naturaleza geométrica, pero con métodos que puedan ser entendidos por un ordenador, y hacerlo de la forma más rápida (con menos operaciones) posible.

Erik y una de las autoras del blog

Erik Demaine no sólo investiga y publica en este área, pero es sin duda en la que más ha participado y gracias a lo cual he tenido el placer de conocer. Este niño grande, curioso y sorprendentemente brillante, fue con 20 años, el profesor más joven del prestigioso Instituto de Tecnología de Massachusetts, M.I.T, o emaití, como se le llama a veces coloquialmente

¿Con 20 años? ¿Sólo con 20 años?

Pues sí, porque aunque Erik detesta que se le tache de niño prodigio, no ha podido evitar ser incluido, por ejemplo, en esta lista, ni ser presentado como tal en la multitud de entrevistas y notas de prensa que sobre él se han publicado desde que era pequeño.

Erik nació en 1981 en Halifax (Canadá), su padre Martin Demaine es una figura capital en su formación ya que pronto se estableció una relación muy especial entre ambos. Cuando Erik tenía sólo 6 años, ambos fundaron la Erik and Dad Puzzle Company una compañía que se dedicaba a elaborar puzzles y pasatiempos. Un año más tarde, padre e hijo decidieron llevar una vida nómada por Estados Unidos y Canadá. El padre era un artista y artesano, sobre todo trabajaba y trabaja el vidrio (ahora como científico en un equipo de investigación del citado MIT, en proyectos que conectan el arte con las matemáticas).

Esta vida nómada les permitía ir de feria en feria, así que Martin decidió dar clases a Erik usando unos manuales de una agencia especializada en la enseñanza no escolarizada. Pronto Erik superó a su padre en muchas materias y a partir de los nueve años fue prácticamente autodidacta hasta que a la edad de 12 años entró en la universidad, consiguiendo titularse a los 14. Obtuvo su doctorado con 20 años y con esa misma edad, como ya se ha dicho, fue el catedrático más joven en la historia del MIT.

Una de las autoras del blog con el padre de Erik, Martin Demaine

En realidad, a la vez que le ofrecían la plaza a Erik, el propio MIT hizo una oferta a Martin, así padre e hijo pudieron seguir trabajando juntos. La labor de ambos está centrada en varios campos como son el arte (donde el padre juega un papel principal), las matemáticas y la informática. Además han conseguido que confluyan estas tres disciplinas cuando han estudiado las matemáticas asociadas al arte del origami (papiroflexia), campo en el que son reconocidos expertos mundiales, incluso tres de sus obras han entrado a formar parte de la colección permanente del Musseum of Modern Art de Nueva York (MOMA). Pero si la vertiente artística de los trabajos de los Demaine es evidente a partir de las imágenes de sus creaciones en papel, el desarrollo por parte de Erik de esta nueva especialidad, el Origami Computacional, es mucho más que eso. Se trata de un esfuerzo interdisciplinar a caballo entre Matemáticas e Informática. Su interés se centra, principalmente, en problemas relacionados con la geometría asociada al plegado de papel con aplicaciones prácticas en campos tan diversos como la manufacturación industrial (fabricación de láminas de metal, bolsas de aire, envoltorios de caramelos), Física (nanoestructuras), o Biología (plegamiento de proteínas).

Erik confiesa que su interés por las matemáticas surgió a partir de los videojuegos. Su padre le comentó que para programar videojuegos tenía que aprender lenguajes de programación y ser bueno en matemáticas y le proporcionó algunos libros empezando por álgebra lineal. En realidad nunca ha abandonado su pasión por los videojuegos y ello le llevo a probar que el juego de Tetris pertenece a la categoría de juegos muy difíciles (es NP-duro encontrar una estrategia ganadora).

Pero además de una mente realmente prodigiosa. Erik es un tío optimista y travieso que disfruta de su trabajo y quiere hacer partícipes a todos de ese goce supremo. No pierde ocasión de bromear sobre hechos matemáticos, como se puede apreciar por ejemplo en esta vídeo en el que, coincidiendo con la celebración del April Fools’ Day (día de las inocentadas), demuestra que P=NP, sufriendo unas terribles consecuencias…

Por último, si se preguntan por qué en todos los congresos la charla de los Demaine e una de las más concurridas de todas, no dejen de ver este vídeo donde además ellos mismos hablan de su historia y hacen… bueno, es mejor que lo vean 😉

Eso sí, este niño grande y brillante es un racionalista incondicional…

There’s nothing Science can’t prove.

Erik Demaine

Tags: Erik Demaine, Geometría Computacional, Martin Demaine, Origami computacional | Almacenado en: Ahora que los niños salieron a jugar...
3 comentarios

¿Estás de broma?¡La bola no entró!

23 de mayo de 2012

–¡Punto mío!

–¿Qué dices, Ven? ¡Ha dado en la línea! ¡Eso es dentro!

–¿¿Dentro?? De eso nada, Sal, ha dado fuera de la línea.

–Ha dado sobre la línea –dijo Sal muy seguro, tranquilo y convencido.

Gauss miraba fijamente la línea tratando de posicionarse en aquella discusión. Pero no lo tenía tampoco muy claro. Al fin y al cabo, adoraba a sus dos dueños y no le gustaba tomar partido. Mati se dejaba querer por el sol y la brisa marina pensando en teoremas y conjeturas.

–Que sí, que ha dado sobre la línea, ¿lo ves? –dijo Sal sin perder los nervios.

–No, Sal, ¡ésa es una marca antigua! –Ven estaba cada vez más rojo y nervioso. Se le empezaba a rizar el pelo, no se sabe muy bien por qué.

–Huy, qué acalorados estáis, chicos –Mati salió de su ensoñación matemática–¿Qué os pasa?

–Nada, Mati –dijo Sal –Sólo que Ven está tratando de hacer trampas…

–Nada de eso, Mati –interrumpió el pequeño muy excitado –Ha dado fuera de la línea, ¡punto mío!

–Que no, Ven, pesado, que ha dado sobre la línea –insistió el gafotas.

–¿¿Estás de broma?? ¡La bola no entró! –Ven estaba cada vez más enfadado, casi tira la raqueta al suelo, pero no lo hizo porque era un regalo de sus abuelos y no quería romperla.

–Entiendo… –añadió la pelirroja tratando de buscar una salida a aquella situación –Todo depende de decidir si el punto donde la bola tocó el suelo estaba sobre una línea o no…

Mati se quedó cómicamente pensando, los niños la miraban esperando, cada uno por su lado, que le diera la razón. Gauss miraba al mar…

–En Matemáticas es mucho más fácil saberlo, ¿sabéis? –comenzó a decir Mati –Se trata simplemente de usar una ecuación.

–¡Toma! Nosotros ya sabemos ecuaciones, Mati –dijo el pequeño con alegría –Nos enseñaste el otro día.

–Es cierto, Ven –respondió Mati –pero las ecuaciones de las que os hablo, son un poco diferentes, aunque también muy sencillas.

–¿Por qué son diferentes, Mati? –preguntó inmediatamente Sal.

–Porque, por ejemplo, en estas ecuaciones, no hay una sola letra misteriosa, o incógnita, la x –dijo Mati –sino que aparece con una de sus mejores amigas, la y, que también va de incógnita.

–Hum, interesante… –añadió Ven –Así que tenemos dos sospechosas…

–Sí y no –contestó ella.

–¿Sí y no? –Sal estaba cada vez más intrigado y entregado.

–Veréis en realidad de lo que se trata es de saber si un punto está o no sobre la línea o recta, que a los matemáticos nos gusta llamar rectas a las líneas rectas, porque hay otras líneas que son curvas –Mati hizo una pequeña pausa y continuó –Para ello lo que solemos hacer es dar una ecuación de la recta, que es, podríamos decir, como una contraseña que deben cumplir los puntos para estar sobre ella.

–¿No hay sospechosos entonces, Mati?

–No exactamente, Ven –continuó la gafotas –No se trata de desenmascarar a x y la y para conocer su valor como hicimos con las ecuaciones del otro día, sino comprobar si el punto que elijamos cumple la ecuación (la contraseña) para estar en esa recta.

Los niños seguían mirando a Mati con los ojos brillantes con las raquetas en ristre, esperando que ella continuara contándoles aquella historia de contraseñas para pertenecer al club de la recta. Gauss se echó a dormir aprovechando que no tenía que ir a buscar las bolas cuando éstas salían despedidas.

–Os lo explico con un ejemplo –propuso Mati mientras sacaba su libreta del bolso de la playa –A ver si así os resulta más fácil

–¡Sí, por favor! –dijo

–Lo primero que necesitamos es un sistema de coordenadas, por ejemplo, cartesianas.

–¿Por qué pones números negativos, Mati? –preguntó Ven.

–Son números enteros, ¿recuerdas? –dijo ella –Para indicar que estamos a la izquierda o por debajo del origen. Los positivos nos indican que estamos a la derecha o arriba del mismo. Y con este sistema de referencia, sabemos las coordenadas de los puntos como cuando jugábamos a los barquitos.

–¡Mola! Como estamos en la playa… –Ven se iba olvidando poco a poco de la polémica bola…

–Voy a dibujar una recta –continuó Mati.

–Para poder conseguir la ecuación de esta recta, es decir, la contraseña para que un punto esté sobre ella, necesito obtener algunos datos de la misma. Para ello vamos a usar, por ejemplo, a dos miembros de ella, dos puntos que pertenecen a este club. Necesitamos las coordenadas de 2 puntos sobre ella…

–Éste y éste –dijo Sal a la vez que señalaba 2 puntos sobre el cuaderno de Mati.

–El (1,1), le llamaremos A…y el (4,3), le llamaremos B –añadió Mati.

–Muy bien. Ahora –dijo la pelirroja –Voy a darle un nombre y un apellido, unas coordenadas, a la flechita que va desde A hasta B. A esa flecha le llamaré vector AB.

–¿Cómo se saben las coordenadas de una flecha, Mati? –preguntó Sal intrigado.

–Las coordenadas de una flecha o vector serán las siguientes: la primera coordenada nos indica cuánto nos movemos hacia la derecha, si es positiva, o hacia la izquierda, si es negativa; la segunda coordenada nos dirá cuántos pasos damos hacia arriba, si es positiva, o hacia abajo, si es negativa.

Los niños se pusieron a contar los pasos que indicaban el vector AB de su dibujo.

–Tres pasos a la derecha… –mascullaba Ven –y dos hacia arriba…¡(3,2), Mati!

–También se pueden calcular las coordenadas del vector AB restando a las coordenadas de B las coordenadas de A –les contó Mati.

–¿Cómo se restan coordenadas, Mati? –quiso saber Sal.

–Ah, claro. La primera con la primera y la segunda con la segunda –respondió ésta.

–Muy, muy bien, chicos –la pelirroja estaba orgullosa de sus amiguitos — Y claro, las coordenadas del punto B es igual a la suma de las coordenadas de A y del vector AB.

–¡Toma, toma, toma! ¡Es verdad! –el pequeño ya estaba alucinando.

–¿Qué pasa si sumamos al punto A dos veces el vector AB? –preguntó ella.

Los niños se quedaron pensando y mirando al dibujo, hasta que, finalmente, Sal dijo:

–Que andaríamos 6 pasos a la derecha y 4 hacia arriba y llegaríamos… a este punto –señaló el gafotas sobre el dibujo –Al de coordenadas (7, 5).

–¿No es el mismo resultado que si hacemos esta cuenta? –cuestionó Mati a los niños.

–¿Cómo se multiplica 2 por (3,2)? –preguntó el gafotas — ¿A la primera coordenada? ¿O a la segunda?

–A las dos –respondió la gafotas.

–¡TOMAAAAAAAAAAAAA! –gritó Ven entusiasmado –Sale (7,5)

–Claro –continuó Mati sonriendo –Todos los puntos de esa recta se pueden conseguir sumando a A el vector AB un número de veces o restándolo.

–¿Cómo que restándolo?

–A ver, ¿hacéis este cálculo? –les pidió

Los niños se pusieron manos a la obra.

–¿Cómo se hace 1-6, Mati? –preguntó el pequeño.

–Andando 6 pasos a la izquierda en la regleta, ¿no te acuerdas? Y 1-4 se calcula dando 4 pasos a la izquierda del 1 también en la regleta.

–Huy, es verdad… –se disculpó Ven –A ver qué nos sale… (-5, -3)… ¡Toma! ¡Es verdad! ¡También está sobre la recta! –el pequeño Ven disfrutaba cada descubrimiento.

–Bueno, pues ya sabemos que para que un punto esté sobre la recta, debe cumplir esa contraseña o condición: que debe ser igual que el punto A más el vector AB multiplicado por un número. O sea que la ecuación que debe cumplir un punto (x,y) para pertenecer a esta recta es la siguiente

–Y eso, ¿cómo se usa, Mati? –preguntó sal muy serio.

–Vamos a ver, decidme un punto sospechoso de pertenecer a la recta…

Los niños miraron el dibujo.

–El (7,5) –propuso Ven McEnroe.

–Muy bien –dijo Mati –tomamos x como 7 e y como 5 y susitituimos en la ecuación. (7,5) pertenecerá a la recta si k nos da el mismo valor en las dos ecuaciones.

–Efectivamente, (7,5) cumple la ecuación, para el valor de k igual a 2. Es un miembro de la recta –concluyó Mati.

–¡Toma, toma, toma! –el pequeño saltaba de alegría.

–Ahora el (10, 9) –propuso Sal animado.

–Vamos a ver si (10, 9) se sabe la contraseña…

–¡Ja! ¡Te pillamos (10,9)! Tú no eres del club de la recta… –Ven estaba disfrutando con aquello.

–Es alucinante, Mati…–Sal miraba al cuaderno y se ajustaba las gafas.

–Las Matemáticas siempre lo son –respondió ella con un guiño –Pero hay otras formas de detectar a los miembros de una recta. Os las enseñaré. Vamos a dejar sola a k en las dos ecuaciones como ya sabemos, deshaciendo en orden inverso todas las operaciones que la ocultan…

–Cuando igualamos las dos ecuaciones porque las dos valen lo mismo, k, tenemos una nueva ecuación de la recta, que se llama ecuación continua.

–Así, cada vez que tengamos dos puntos de una recta podemos calcular suu ecuación continua sin más que hacer esto

–¡Qué chulo! –exclamó Sal — ¿¡Cómo la usamos para saber si, por ejemplo, el (1,0) pertenece al club?

–Muy fácil –dijo Mati –Cambiamos x por 1 e y por 0 y vemos qué pasa.

–Ajá, no eres de nuestro club, forastero… –dijo Ven cuando descubrieron que el (1,0) no pertenecía a la recta.

–¿Os gusta, chicos? –continuó la pelirroja –Pues aún podemos escribir la ecuación de la recta de otra forma.

–¡Venga! –la animó Sal.

–Usando nuestras técnicas de desenmascaramiento vamos a tratar de llevar todo al primer miembro de la ecuación, ya veréis…

–Ya tenemos otra ecuación de la recta –dijo Mati –La ecuación implícita.

–Prueba con el (4,2), Mati –pidió Ven ansioso.

–¡¡Yo! ¡Yo lo hago! –intervino Sal –Cambio x por 4…cambio y por 2…

–¡Otro! Hemos pillado a otro que no está –Ven lo pasaba en grande.

–Pues además de decirnos si un punto pertenece o no a una recta, con esta ecuaciones podemos calcular todos los puntos sobre ella que queramos –dijo Mati.

–¿¿Cómo?? –preguntaron los dos niños a la vez.

–Elegid un valor para la x –les propuso.

–¡10! –gritó Ven.

–Estupendo –contestó la pelirroja –ponemos 10 en lugar de x y vamos a ver cuánto vale y…

–¡Toma, toma, toma! ¡CÓMO MOLA! –a Ven se le salían los ojos de las órbitas.

–¡Me encanta, Mati! –Sal estaba también entusiasmado.

–Pues aún hay más…–respondió ella con tono de misterio –pero ésas la dejaremos pendientes... Ahora vamos a dar un paseo por la playa.

–¡Vale! –dijo Ven –Pero que sepáis que la bola no entró…

Tags: coordenadas cartesianas, ecuación de primer grado, ecuación lineal, ecuaciones de la recta | Almacenado en: La hora de las tareas
8 comentarios

Matemáticas y xenofobia

21 de mayo de 2012

La matemática posee no sólo verdad, sino belleza suprema; una belleza fría y austera, como aquella de la escultura, sin apelación a ninguna parte de nuestra naturaleza débil, sin los adornos magnificos de la pintura o la música, pero sublime y pura, y capaz de una perfección severa como sólo las mejores artes pueden presentar. El verdadero espíritu del deleite, de exaltación, el sentido de ser más grande que el hombre, que es el criterio con el cual se mide la más alta excelencia, puede ser encontrado en la matemática tan seguramente como en la poesía.

Bertrand Russell

Después de leer esta cita de Russell es difícil creer que algo tan sumamente bello y sublime pudiera ser usado en pro de algo tan deshumanizado como la xenofobia, pero, citando a otro grande, cosas veredes, amigo Sancho, que farán fablar las piedras… (Cita, por cierto, frecuentemente atribuida al Quijote, aunque hay quién apunta que es aún más antigua).

Lamentablemente, sí.

Ahora pega aquí aquella cita célebre de Plauto sobre lobos y hombres

Lobo es el hombre para el hombre, y no hombre, cuando desconoce quién es el otro

Tito Maccio Plauto

Hoy voy a compartir con vosotros una historia donde las Matemáticas fueron usadas, lamentablemente, como herramienta para llevar acabo una purga absolutamente xenófoba.

Conocí la historia por un artículo que llegó a mis manos a través de Twitter, «Los problemas judíos», podéis encontrarlo también en SlideShare.

Lo que Tanya Khovanova nos desvela en su artículo, Los problemas judíos, es una colección de problemas que el Departamento de Matemáticas de la Universidad Estatal de Moscú proponía a los aspirantes judíos a dicha Universidad, para evitar que éstos u otros grupos de personas indeseables accedieran a ella. Para evitar reclamaciones y/o impugnaciones al proceso, todos estos problemas tiene una solución muy sencilla pero difícil de encontrar, puesto que era necesaria una idea feliz que te condujera trivialmente a resolverlo. Nadie podía alegar que eran ejercicios irresolubles o muy complicados…

Estos problemas son conocidos también con los intuitivos nombres de ataúdes o asesinos. Y sí, muchos aspirantes judíos a la citada universidad tuvieron que enterrar sus aspiraciones en alguno de estos ataúdes hechos, no de madera de pino, sino perversamente construidos con Matemáticas.

Si uno intenta resolver algunos de estos problemas, puede que no le resulten tan complicados, pero hay que decir que el procedimiento para estos aspirantes era ir resolviendo un problema tras otro hasta fallar en alguno, momento en el que eran eliminados, con lo que las condiciones de contorno eran peores que las que tenemos nosotros en casa si lo intentamos por el puro gusto de resolver un reto matemático.

Por poner un ejemplo sobre uno de estos problemas ataúdes propuestos a modo de Selectividad a aquellos alumnos judíos, vemos éste:

Problema 20:

Construir (con regla y compás) un cuadrado conocidos un punto de cada uno de sus 4 lados.

Vamos a ver cómo se resuelve este problema para ver que efectivamente no es tan complicado y, de paso, por si queréis proponerlo sobre una servilleta en un restaurante mientras os sirven la comida. Pero, por favor, con ningún fin xenófobo.

Lo que tenemos como dato de entrada son 4 puntos que podemos llamar, echando mano de nuestra originalidad e imaginación, A, B, C y D, y sabemos que cada uno de ellos está sobre el lado de uno de los lados del cuadrado buscado. Se trata, por lo tanto, de dibujar, usando regla y compás, dicho cuadrado.

Para ello, primero trazamos el segmento que une los puntos A y C.

A continuación, desde el punto B, trazamos un segmento perpendicular al segmento AC, y ponemos un punto D’ sobre ese segmento, de forma que la distancia entre B y D’ sea la misma que entre A y C. Ése nuevo punto, D’, está sobre el mismo lado del cuadrado que D, es cuestión de análisis de ángulos.

Ya tenemos la orientación de uno de los lados del cuadrado, la de la recta que pasa por D y D’. Se trata simplemente ya de dibujar la recta DD’, una paralela a ésta por B y dos perpendiculares a la misma, una por A y otra por C ….

Y así se obtiene el cuadrado buscado.

Hay muchos más problemas judíos, ataúdes o asesinos. Si queréis ver más os recomiendo este trabajo de Khovanova y Radul que fue el que me descubrió la existencia de los mismos.

Lo que me apena de esta historia es el hecho de que estos problemas tan bellos hayan sido cómplices de la maldad humana y lo que me inquieta es que no es una historia tan antigua, de hace poco más de 40 años. Esta página de la misma Tanya Khovanova aporta enlaces a documentos sobre este espisodio.

Sobre este mismo asunto, se ha publicado el libro You failed your math test, Comrade Einstein: adventures y misadventures of young mathematicians en el que el matemático Ilan Vardi presenta y compara los problemas mencionados en esta entrada con los de la Olimpiada Matemática del año 2000. Incluye además un ensayo El genocidio intelectual explicando el trasfondo histórico de esta práctica llevada a cabo en la URSS en las décadas de los 70 y 80.

Nuestra historia también tiene su heroína, Bella Abramovna Subbotovskaya, que ante esta situación de injusticia con los judíos fundó en 1978, con ayuda de otros colegas, la Universidad del Pueblo Judío cuyas primeras clase se impartieron en el propio apartamento de Subbotovskaya. Sus amigos la describen como fuerte, enérgica y reivindicativa, al mismo tiempo que cálida, bondadosa y optimista. Todos resaltan su enorme determinación. Bella murió, de forma extraña, cuando sólo tenía 44 años.

George G. Szpiro, escribió en este artículo, Bella Abramovna Subbotovskaya and the Jewish People Unniversity, esto sobre ella:

Hace exactamente hace 25 años, el 23 de septiembre de 1982, alrededor de las 11 de la noche, en una calle oscura de Moscú, se produjo un accidente. Una mujer caminaba por la acera. Acababa de visitar a su madre y volvía a su casa. Aquella era una calle tranquila por la que, rara vez, pasaba un vehículo a esa hora. De repente, apareció un camión a gran velocidad, atropelló a aquella mujer y se dio a la fuga. Minutos más tarde, otro coche se detuvo junto a la víctima unos instantes y también desapareció. Apareció una ambulancia, ¿quién la llamó?, y llevó a la víctima directamente a la morgue. El funeral se celebró al día siguiente, en privado. Nadie habló, no se pronunció ningún elogio. Los asistentes al mismo sólo cuchicheaban entre ellos, observados por algunos hombres con aspecto de oficiales. Al final del funeral, todos se dispersaron en silencio. El conductor de aquel camión que se había dado a la fuga nunca fue hallado y se cerró el caso. Aquel accidente tenía todos los ingredientes de un golpe de la KGB.

La víctima fue Bella Abramovna Subbotovskaya, una matemática de 44 años. Los días previos a su muerte había sido convocada en varias ocasiones por la KGB y sometida a interrogatorios. El crimen sobre el cuál fue interrogada fue la creación de la Universidad del Pueblo Judío

Hasta aquí lo que sé de esta historia. Otra muestra más de la estupidez humana y ese afán de etiquetar a los humanos y clasificarlos en grupos en función de criterios tan absurdos como etnias, ideologías…o incluso por sus preferencias a la hora de practicar sexo. No concibo, posiblemente sea torpe, cómo puede etiquetarse una persona en función de su tendencia sexual. Si ya no lo entiendo cuando se le intenta etiquetar en función de su pasaporte o el color de su piel, que es el mismo 24 horas al día, ¿cómo podría hacerlo en función de algo puntual y absolutamente íntimo? En fin… A veces pienso que no somos tan inteligentes como pensamos. El caso es que este tipo de decisiones me inquieta y me producen nerviosismo y desasosiego, y me evocan, irremediablemente, historias terribles que todos conocemos sobre discriminación llenas de sufrimiento y dolor humano.

Tags: Los problemas judíos, Xenofobia | Almacenado en: Ahora que los niños salieron a jugar...
18 comentarios

Esa letra tan sospechosa…la x

16 de mayo de 2012

–Me parece que…va a ser la señorita Amapola…

–Ven, no digas tus sospechas en voz alta…

–¿Voy bien, Sal?

–No se puede hablar, Ven, concéntrate en el juego.

–Es que ya sé quién y con qué, creo, vamos, porque el candelabro…

–Te recuerdo que tienes que resolver las 3 incógnitas.

–Ya, ya lo sé, ¡me encantan las incógnitas!

–¡Y a mí! –Mati acababa de llegar.

–¡Hola, Mati! –saludaron los dos niños con alegría.

–¡Hola guapos! Cuando os escuché pensé que estabais resolviendo ecuaciones –dijo la pelirroja guiñando un ojo.

–No, no, estamos jugando al Cluedo –respondió Ven –Yo soy el profesor Mola –concluyó con una sonrisa de pícaro.

–El profesor Mora, Ven –le corrigió su hermano.

–No, el profesor Mola, que mola más –el pequeño cerró los ojillos y sonrió apretando los dientes mostrando la última baja de su dentadura.

–¿Qué son ecuaciones, Mati? –preguntó Sal que no había dejado de pensar en aquella palabra que ella había dicho.

–Una ecuación es, más o menos, como un Cluedo matemático… –comenzó diciendo la gafotas.

–¿Con sospechosos? –preguntó Ven con los ojos como platos.

–Bueno, las más sencillitas, con sospechosa, la x –dijo Mati.

–¿La x? ¿La letra x? ¿O hay un número especial como π que se llama x? –la cabecita de Sal comenzaba a dar vueltas.

–¿Queréis que os enseñe a resolver unas ecuaciones de las más sencillas? Es casi como jugar a los detectives –propueso ella.

–¡Sí! –respondieron los niños provocando un sobresalto al pobre Gauss que estaba mirando el tablero del juego con cara de detective sagaz.

–Os voy a proponer un caso que tendréis que resolver como buenos detectives. Tendréis que desenmascarar a la x para ver quién se esconde bajo esa máscara –añadió Mati hablando lentamente con voz misteriosa.

–Tranquila, pequeña, estás frente a los 2 mejores detectives del mundo… –respondió Ven haciéndose el interesante.

–Comencemos, señora, ¿qué sabe del caso? –continuó Sal en su papel de sabueso.

–Pues sé que la sospechosa fue vista primero multiplicada por un 4 –comenzó Mati con voz de miedo e indefensión –Más tarde se le sumó un 3…

–Hum, qué mal huele este asunto… –interrumpió Ven.

–Un testigo me dijo que todos juntos eran iguales que un 39 –terminó de decir ella.

–¿Algo más, señora? –preguntó Sal mirando por encima de sus gafotas.

–No, señor detective, es todo lo que sé ¿Podrán resolver el caso?

–Ni idea… –respondió Ven desmoralizado.

–Podemos ir probando… –empezó Sal –Esa x, ¿es un número natural o puede ser negativo? ¿Podría ir con decimales?

–¿Cuáles eran los naturales? –preguntó Ven –Los que sirven para contar, ¿no?

–Eso es, Ven –respondió Mati –Veo que recuerdas el cuento con las ovejitas y los conjuntos numéricos –continuó sonriendo — Sí, Sal puede ser negativo y puede tener decimales. Por lo tanto, probando, puede que no acabaras nunca… Se puede hacer más rápido, ¿queréis que os enseñe?

–¡Sí! –la respuesta de los niños estaba clara.

–Pues bien, vamos escribir en nuestra libreta todos los datos que tenemos. Sabemos que iba multiplicada por 4, que se le sumó un 3 y que todos así eran un 39. Escribamos todo esto. Como tenemos que escribir la letra x, para no confundirnos con el signo de multiplicar, éste, el signo de multiplicar lo escribimos como un puntito.

–Esto que hemos escrito es una ecuación. Una ecuación lineal con una incógnita. La llamamos lineal porque las incógnitas, en este caso, sólo una, la x, aparece sin estar elevada a ninguna potencia. Porque en otras ecuaciones, las incógnitas pueden aparecer aún más enmascaradas elevadas a otras potencias:2, 3… –les explicó Mati –Para desenmascarar a la x, que es nuestra incógnita, vamos a deshacer todo lo que ella hizo, en orden inverso, hasta conseguir llegar hasta 39. Para ello, como lo último que hizo fue sumarse un 3, vamos a deshacerlo restando, que es la operación inversa de la suma. Pero, ¡ojo!, tenemos que restar lo mismo en los 2 lados del signo igual. Vamos a llamar primer miembro a lo que aparece a la izquierda del signo igual y segundo miembro al que aparece a la derecha. Como los dos miembros son iguales, vamos a ir haciendo las mismas operaciones en los 2 hasta que consigamos dejar sola a la x y así poder descubrir quién es, ¿vale? si no hacemos lo mismo en los dos miembros estaremos destruyendo pistas de la escena.

–¡Vale! ¡Qué emoción! –Ven estaba excitado, Sal miraba sin pestañear, Gauss seguía mirando el tablero del Cluedo. Es un perro un poco raro…

–Si restamos 3 en ambos miembros, llegamos a la conclusión de que 4 multiplicado por x es igual que 36 –siguió la pelirroja.

–Se te olvidó poner el punto entre 4 y x –dijo Ven,

–Sí, pero en realidad, en Matemáticas solemos hacerlo. Si no escribes ningún signo se entiende que estás multiplicando, y en realidad, expresa mejor lo que queremos decir. Es decir, decimos 4x y pensamos en eso, en que tenemos 4 veces a la x.

–Me gusta –dijo Sal –¿Y ahora?

–Ahora, como la x se ha escondido multiplicándose por 4, la sacamos de su escondite con la operación inversa a la multiplicación –siguió Mati –¿Qué es lo inverso de multiplicar?

–¡Dividir! –dijeron los hermanos al unísono.

–Efectivamente, chicos. Dividimos los dos miembros por 4 para desenmascarar a la sospechosa…

–¿Por qué tachas los 4s, Mati? –preguntó el gafotas.

–Porque multiplicar y dividir un número, en este caso la x, por el mismo número, es como multiplicar por 1, o sea, no hacer nada.

–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven excitado –Sabía que había sido el 9… A mí no se me engaña tan fácilmente…

–No mientas, Ven… –respondió su hermano –Me gusta mucho, Mati ¿nos propones otro caso?

–¡Claro! Nuestra siguiente sospechosa fue un día vista multiplicada por 7 y a ese producto le restaron 4. Al día siguiente, vieron que primero se multiplicó por 4 y después se sumó 5. Ahora viene lo interesante, los dos días llegó al mismo resultado –les contó Mati con voz muy misteriosa.

–Y, dígame, señora, ¿cuál era ese resultado? –preguntó Sal Holmes.

–Nadie lo recuerda –dijo Mati bajando la voz hasta el susurro.

–Entonces no podremos ayudarla, señora –añadió Ven Watson.

–¿Están seguro de ello mis sabuesos? –preguntó Mati.

–Absolutamente –confirmó el pequeño Watson.

–Si me permiten ayudarles… –Mati guiñó un ojo.

–Por favor… –dijo Sal haciendo una pequeña reverencia cómica.

–Vamos a escribir lo que sabemos en nuestra libreta de detectives.

–Pero, ahora, la x está en los 2 miembros de la ecuación –dijo Sal angustiado.

–Efectivamente, Sal. Tenemos 7x en el primer miembro y 4x en el segundo. Vamos a llevarlas todas al primero quitándolas del segundo. como el segundo tiene 4x, restamos 4x en los dos, siempre en los 2 para no destruir pistas.

—7x menos 4x son 3x y ya tenemos una ecuación como la de antes –dijo sonriendo la pelirroja.

–Déjanos a nosotros, Mati, por favor –pidió Sal.

–Toda vuestra, chicos –respondió ella.

–Suma 4 en los dos miembros, Sal –dijo Ven a su hermano excitado –Para delatarla.

—¡Ahora divide por 3, para dejarla sola! –gritó Ven.

–¡Toma, toma, toma! –Ven estaba excitado. Sal no podía dejar de sonreír. Sí, Gauss seguía mirando el tablero del Cluedo. Él es así.

–Pero, bueno… Sois los mejores detectives del mundo –dijo Mati sonriendo orgullosa –¿Os atrevéis a resolver ésta?

Los dos niños se pusieron manos a la obra mientras Gauss…bueno, ya sabéis dónde seguís nuestra mascota.

–Huy, ¿ahora qué hacemos Sal? –preguntó el pequeño preocupado.

–Pues..yo creo que si la x se ha dividido por 4, para delatarla hay que hacer lo contrario de dividir… –pensaba Sal en voz alta — es decir, multiplicar por 4 ambos miembros.

Ven buscó la confirmación en la mirada de Mati que asintió con un guiño y una sonrisa.

–¡Toma, toma, toma! ¡Cómo molan las ecuaciones! –Ven saltaba sobre sus pies.

–Mucho. Es como jugar al Cluedo –en la cara de Sal lucía una enorme sonrisa.

–Me alegro mucho de que os gusten –añadió Mati –Otro día os explicaré otras ecuaciones si os apetece.

–¡Claro que nos apetece! –respondió Sal.

–Venga, ¿jugamos una partida al Cluedo, chicos?

–Vale, pero vamos a fastidiar a Gauss que parece que está a punto de resolver el caso anterior…

Tags: ecuación de primer grado, ecuación lineal | Almacenado en: La hora de las tareas
9 comentarios