Ahora que los niños salieron a jugar… | Mati, una profesora muy particular

Archivo de la categoría ‘Ahora que los niños salieron a jugar…’

¿Jugamos?

24 de septiembre de 2012

El sábado 22 de septiembre a las 16h 49m (hora oficial peninsular) llegó el otoño. Hacía mucho calor en Sevilla, de hecho, creo que no nos hubiésemos enterado de no ser por la prensa. Eso sí, oscurecer ya había oscurecido desde el día antes, tras el consejo de ministros…

Como en una especie de ritual de despedida me puse a repasar las fotos del extinto verano, por si me servía, además, para no pensar, en una tarde de sábado, en la desafortunada, según mi opinión, LOMCE…

Este repaso me llevó a una ciudad francesa en la que estuve, casi fugazmente, este año (¿sabrías reconocerla sólo mirando la foto? 🙂 ) Como quiera que al mirar las fotos recuerdas el viaje en sí, aparte de recordar una cena sin indeterminaciones de ningún tipo en la plaza de l’Hôpital de dicha ciudad (esto es un chiste un pelín frikie matemático), recordé una velada con unos amigos en la que, entre otras cosas, descubrí un juego de mesa hasta entonces desconocido para mí. Tengo que reconocer que no conseguí ganar ni una sola vez a mi oponente y que mi orgullo quedó bastante perjudicado, perder ante un físico teórico en un juego diseñado por un matemático…

Esa es la historia que me ha llevado a escribir hoy sobre el juego en cuestión. No, no se trata de hacer publicidad, no hay niguna intención comercial. De hecho, como vais a ver, se puede fabricar uno en casa sin ninguna dificultad.

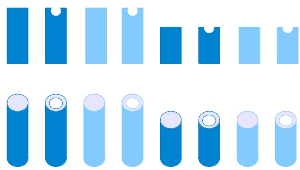
Se trata de el juego de mesa llamado Quarto! Este juego de mesa diseñado por el matemático Blaise Muller, es un juego de estrategia para dos jugadores. Para jugar sólo necesitamos una tablero de 4 x 4 casillas y de 16 piezas o fichas, cada una de ellas con cuatro características:

Color: sólo hay dos colores posibles, en las de la foto del juego, claro y oscuro.

Tamaño: pequeña o grande.

Forma: cilíndrica o paralelepípeda.

Punta:lisa o agujereada.

En la siguiente figura os dejo un esquema con todas las fichas necesarias, manifiestamente mejorable, lo sé…

Como os dije, se puede fabricar en casa, con pocos materiales. Hay varias versiones del juego, pero digamos que la básica consiste en que cada turno, uno de los jugadores elige una de las piezas (que no hayan sido usadas previamente, claro) y la coloca en una de las 16 casillas del tablero. El objetivo es conseguir alinear (en horizontal, vertical o diagonal) 4 fichas con alguna característica en común, esto es, o cuatro del mismo tamaño, cuatro del mismo color, cuatro con la misma forma o cuatro con la misma punta y gritar ¡Quarto! En la siguiente figura se muestran algunas combinaciones ganadoras posibles, según cada una de las cuatro características anteriormente descritas.

Hasta aquí puede parecer una versión más elaborada del clásico 4 en raya. Para esta versión del Quarto, la más simple, ya hay quien encontró estrategias ganadoras para el jugador que empiece en segundo lugar.

Pero el juego da mucho más de sí… Una primera variante de esta versión, la que se juega habitualmente, se conoce como la versión twist, en la que, en cada turno, cada jugador jugará la pieza que le dé su oponente. Así me lo contaron directamente a mí. Pero esta versión, aunque más elaborada, si se juega a la defensiva nos llevará casi sistemáticamente a tablas.

La variante del juego en la que fui vilmente vilipendiada consiste en una versión twist, es decir, tienes que jugar la ficha que te ofrece tu oponente, y en la que el objetivo es conseguir que cuatro fichas con alguna característica en común, formen un cuadrado sobre el tablero, no una línea. A continuación, algunas posibles cuadrados que se pueden conseguir en el tablero del Quarto.

Reconozco que no he vuelto a jugar desde aquel viaje, pero al ponerme a escribir esta entrada me han entrado unas ganas irrefrenables no sólo de jugar sino de intentar estudiar estrategias ganadoras para el mismo, por si tengo la oportunidad de la revancha… Bicheando por la red no he encontrado más trabajos que le que se enlaza más arriba, aunque reconozco, también, que no he tenido tiempo de bucear muy profundo. Lo haré, a Euler pongo por testigo…

Ya sabéis cómo construir el juego y algunas de las posibles variantes que podéis jugar en una tarde lluviosa de otoño, porque espero que llueva y mucho, sólo nos falta que también tengamos este año sequía…

A continuación lo que os voy a proponer tiene que ver un poco con la variante de los cuadrados, y es un pequeño reto de ésos que podéis compartir en la servilleta del café 😉

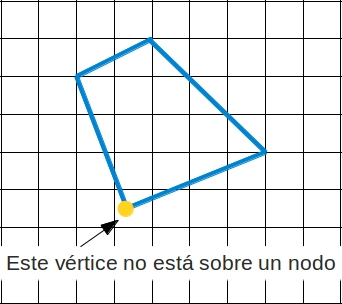
Tenemos un tablero de 5 x 5, para que sea un poco más interesante y entretenido, la pregunta es ¿de cuántos tamaños diferentes son los cuadrados que se pueden formar? Venga, os dibujo uno para que no digáis que no os doy pistas…

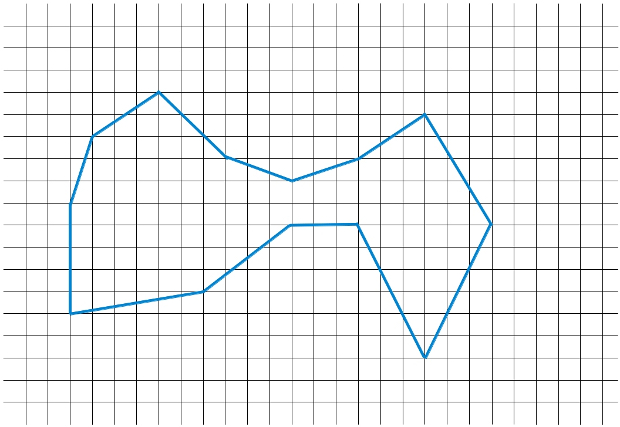
Y una segunda pregunta, ¿cuántos cuadrados diferentes se pueden formar? Ahora sí contamos los cuadrados que tengan el mismo tamaño pero estén en distinta posición, como por ejemplo, los dos de la figura de la izquierda. El cuadrado rojo y el azul tienen el mismo tamaño, sí, pero están en dos posibles situaciones. Ea, pues ¿cuántos en total se pueden formar?

Pues bien, esto también nos da para un juego de lápiz y papel para dos o más jugadores, sencillo y barato, que está la cosa mu mala. En un papel cuadriculado, cada jugador, por turnos, marca con su color una de las casillas y quedará eliminado aquel que complete un cuadrado con 3 casillas ya marcadas, ganando el último jugador que quede en el juego.

¿Jugamos?

P.S.: Traté de comprar el juego en aquella ciudad francesa en una tiendecita que me recomendaron, estaba cerrada. Pero aún sonrío cada vez que veo el cartel que anunciaba el cierre, todo siempre se puede decir mejor, con humor…

Cerrado por enfermedad ¡Reabriremos lo más rápido posible! (Excepto en caso de enfermedad mortal, consulten las necrológicas)

Tags: Blaise Muller, Juegos, Quarto! | Almacenado en: Ahora que los niños salieron a jugar...
2 comentarios

Papel cuadriculado y George Pick

17 de septiembre de 2012

De nuevo es lunes y de nuevo tenemos que enfrentarnos a una semana marcada por las noticias poco esperanzadoras, aunque eso irá cambiando poco a poco… les quedan pocos medios que controlar. Como estamos todos un poco saturados de esto, os voy a contar un pequeño entretenimiento matemático para que podáis compartir sobre una servilleta a la hora del café.

Para nuestro siguiente truco sólo vamos a necesitar papel cuadriculado y lápiz, o bien dibujar una malla cuadriculada sobre la servilleta en cuestión. Intentaremos que la malla cuadriculada sea lo más uniforme posible, y aceptamos que cada cuadradito tiene área 1. A los cruces entre las líneas horizontales y verticales de la cuadrícula los llamamos nodos.

Ahora vamos a pintar un polígono sobre la malla siguiendo las siguientes reglas:

a) Los vértices del polígono deben estar situados sobre nodos de la cuadrícula. El polígono de la figura no es válido, por ejemplo.

b) Debe ser un polígono simple, es decir, que los lados del polígono no se crucen entre ellos, como, por ejemplo en la siguiente figura que representa a un polígono no simple.

Pues bien, podemos dibujar un polígono como el siguiente:

Atención, pregunta: ¿Cuál es el área del polígono de la figura anterior?

Evidentemente, tenéis la opción de dividir el polígono en otros más simples, triángulos y cuadriláteros, para los que conocéis las fórmulas correspondientes para calcular sus áreas y responder a la pregunta planteada o bien, usar la Fórmula de Pick, que es bastante más rápido.

¿Que cuál es la fórmula de Pick? Claro, se me olvidó ese pequeño detalle… El Teorema de Pick (1899) establece que si tenemos un polígono simple cuyos vértices tienen coordenadas enteras, es decir, cuyos vértices están sobre los nodos de la cuadrícula y llamamos B al número de nodos sobre la frontera del polígono e I al número de nodos de la cuadrícula en el interior del polígono, entonces el área A del polígono se puede calcular con la fórmula:

Vamos a ver que, efectivamente, esta fórmula funciona con polígonos sencillos para los que sabemos calcular sin dificultad el área.

En la siguiente figura, tenemos un rectángulo, de base 4 y altura 6 (os recuerdo que cada cuadradito de nuestra malla tiene área 1), por lo tanto, es un rectángulo de área 24; el triángulo central tiene una base de longitud 8 y una altura de 6, su área es de 24, también; y por último, el cuadrado de la derecha, tiene un lado de longitud 3 lo que nos da un área de 9.

Vamos a calcular sus áreas según la fórmula de Pick, para ello hemos señalado en rojo los nodos de la frontera, los que nos dan el valor de B y en verde, los nodos interiores al polígono, que nos darán el valor de I y… ¡tachán!

En realidad, no hacía falta esta comprobación puesto que el Teorema de Pick está rigurosamente demostrado y publicado en su trabajo Geometrisches zur Zahlenlehre, publicado en Praga en 1899. Lamentablemente, este trabajo de Pick pasó sin pena ni gloria y fue Hugo Steinhaus (al que, por cierto, le dirigió la tesis doctoral nada más y nada menos que Hilbert), el que lo dio a conocer, ya en 1969.

George Pick

George Pick nació en Viena en 1859, en el seno de una familia judía, lo que sin duda le allanó el camino para poder morir en el campo de concentración de Theresienstadt, unos 60 kilómetros al norte de Praga. Aunque, posiblemente, lo más conocido de los trabajos de Pick, sea la fórmula presentada, llegó a publicar 67 artículos que abarcaban temas tan diversos como el Álgebra lineal, el Análisis funcional, el Cálculo Integral o Geometría, aunque su atención se centraba, principalmente en Funciones de variable compleja, Ecuaciones diferenciales y Geometría diferencial.

Además de lo anterior, a Pick le corresponde el honor de haber introducido al mismísimo Albert Einstein en los trabajos de Cálculo Tensorial de Ricci y Levi-Civita, que sirvieron más tarde a don Albert, en 1915, para formular su teoría de la relatividad general. El propio Einstein escribía en una carta a Levi-Civita:

«Admiro la elegancia de su método de cálculo, debe ser agradable pasear a través de estos campos a lomos del caballo de las matemáticas reales, mientras nosotros tenemos que hacer nuestro camino trabajosamente a pie»

Volviendo a nuestro protagonista de hoy, Pick, parece que él y Einstein fueron grandes amigos, compartiendo además la pasión por la música.

¿Y bien? Volviendo al reto del principio, ¿qué área tiene el polígono grandote que os presenté? Venga, va, os echo una mano por si no os pinta el boli, os coloreo los puntitos 😉

Tags: Áreas de polígonos, Einstein, Fórmula de Pick, George Pick, Levi-Civita, Ricci, Teorema de Pick | Almacenado en: Ahora que los niños salieron a jugar...
4 comentarios

El legado de Alan Turing

10 de septiembre de 2012

A pesar de ser un personaje absolutamente decisivo en el desarrollo de la Segunda Guerra Mundial (sin él posiblemente hubiera durado más, con más pérdida de vidas, con más sufrimientos), a pesar de ser uno de los padres de la Computación (tanto a nivel teórico como práctico), a pesar de haber revolucionado completamente el criptoanálisis, a pesar de una vida agitada y controvertida, la figura de Alan Turing no ha empezado a ser conocida por el público (fuera de los círculos académicos) hasta hace relativamente poco.

Efectivamente, Alan Turing que nació en Inglaterra hace justamente cien años (es por ello que este 2012 es considerado internacionalmente como el año Turing) lideró el grupo de criptoanalistas británico que consiguió descifrar los mensajes alemanes que usaban la máquina Enigma que se creía inexpugnable. Para conseguir dicho objetivo realizó hasta cinco aportaciones fundamentales al criptoanálisis y participó en el diseño y construcción de Colossus lo que muchos consideran el primer ordenador de la historia. El software (aunque no existía software tal y como hoy lo conocemos) de Colossus fue obra del propio Turing y, sobre todo, de Bill Tutte, muy conocido posteriormente por sus aportaciones a la Teoría de Grafos. sí, si no hablo de grafos me da algo… 😉

Pero el interés de Turing por el criptoanálisis y la informática teórica (sobre todo a esta última) es anterior a la Segunda Guerra Mundial ya que una de sus aportaciones decisivas procede de 1936 cuando publicó un artículo que es una de las bases de dicha disciplina y que supuso el nacimiento del diseño de ordenadores con programas almacenados. En dicho artículo se describe lo que posteriormente se ha llamado una máquina de Turing.

Una máquina de Turing (que es un mero ejercicio mental, no una máquina real) básicamente está constituida por una cinta infinita dividida en casillas contiguas en las que podemos escribir un 0 o un 1 (o no escribir nada) y una cabeza lecto-escritora; esta máquina está gobernada por un programa (sucesión finita de instrucciones) que llevará a la cabeza lecto-escritora a realizar distintas operaciones simples (leer lo que pone la casilla correspondiente, moverse un lugar hacia la izquierda o la derecha, cambiar el valor de la casilla o dejarlo tal y como está). Uno puede pensar que una máquina tan simple está muy limitada, sin embargo es comúnmente aceptado que todo lo que puede hacer un ordenador moderno puede ser realizado por una máquina de Turing. El trabajo en el que Turing presentó su modelo de máquina teórica sentó las bases de lo que es conocido como arquitectura Von Neumann (que perdura hoy en día dividiendo un ordenador en software y hardware) y constituye uno de los tres trabajos fundamentales (y en cierto sentido equivalente) de la teoría de la computación (los otros dos son el famoso teorema de Gödel y el trabajo de Alonzo Church).

Aquí puede verse una máquina de Turing construida con LEGO. Y aquí, la edición de Monopoly en honor a nuestro personaje de hoy.

Pero más que de su máquina, vamos a hablar un poco sobre él. Como dijimos al principio, Turing fue un personaje decisivo en el desarrollo de la Segunda Guerra Mundial ya que fue uno de los líderes de Bletchley Park y sus trabajos permitieron descifrar la mayoría de los mensajes que se transmitían los alemanes. Con ello los aliados disponían de información de primer orden que fue usada en innumerables ocasiones para prepararse ante ataques alemanes o para infligir pérdidas en los flancos más débiles del enemigo. De hecho, su relación con la Inteligencia Militar británica comienza en septiembre de 1938 (un año antes de la guerra). Durante la guerra su labor se centró en descifrar los mensajes elaborados con la máquina Enigma (usada por la marina alemana), para ello diseñó el llamado Bombe, un precursor de los ordenadores diseñado con el objetivo específico de desencriptar mensajes de Enigma. El primer Bombe entró en funcionamiento a comienzo de 1940 y al final de la guerra había más de doscientas bombas funcionando a pleno rendimiento.

En un ambiente excéntrico con tantos científicos reunidos como era el de Bletchley Park, Turing tenía fama de excéntrico, o sea que… Una de sus excentricidades consistía en desplazarse a veces corriendo hasta Londres para las reuniones de alto nivel a las que era convocado (Londres está a 60 km de Bletchley Park), ya que era un fanático de recorrer largas distancias corriendo, lo que le llevó a ser un gran maratoniano (su marca en 1949, ya con 37 años, estaba alrededor de las 2 horas y 45 minutos lo cual era sólo unos 10 minutos más lento que el campeón olímpico de la época).

Alan Turing de niño

Aunque al fin y a la postre, la excentricidad que posiblemente llevaría a Turing a su muerte fue su carácter de homosexual. A través de una denuncia que presentó por un robo que había sufrido en su hogar (por parte de un amante ocasional), su homosexualidad salió a la luz y por la misma ley por la que fue juzgado Oscar Wilde más de cincuenta años antes se le ofreció o bien una pena de cárcel o una castración química; optó por esta última y se le presentaron una serie de efectos secundarios que algunos consideran como una de las causas que lo llevó al suicidio en 1954.

Respecto a su suicidio, existen varias leyendas y algunos puntos oscuros. La autopsia determinó que se produjo por envenenamiento con cianuro, junto a su cadáver se encontró una manzana a medio comer, pero la manzana nunca fue analizada y por tanto se desconoce si fue la fuente del envenenamiento. Naturalmente, estos puntos oscuros han motivado el nacimiento de muchas sospechas, pero puesto que su cadáver fue incinerado, es posible que nunca podamos llegar a la certeza de qué fue lo que realmente ocurrió, aunque no faltan voces que afirmen que no fue algo voluntario…

Por cierto, si os interesa la figura de Turing, tanto el personaje como sus aportaciones a la Computación, Criptografía, Ingeniería o incluso a la Biología, este año, en Madrid, la Real Academia de Ciencias y la Fundación Areces (Madrid) han organizado el mayor evento alrededor de nuestro personaje celebrado en España en este año de Turing. La inscripción es gratuita y tenéis información sobre El legado de Alan Turing aquí y aquí ¿Nos vemos allí?

Tags: Alan Turing, El legado de Turing | Almacenado en: Ahora que los niños salieron a jugar...
30 comentarios

Llegó Septiembre y hablamos de medidas, pero no de las del gobierno

03 de septiembre de 2012

Hace un par de días llegó el 1 de Septiembre de 2012. Como 1 de Septiembre, sin más, era el día temido por aquellos que tenemos hasta el 31 de Agosto de vacaciones. Con el apellido de 2012 se nos han unido a nuestras cuitas todos y cada uno de los consumidores que hemos visto reducir nuestro poder adquisitivo y de paso nuestra calidad de vida. También por los empresarios que nos proveen de servicios no de primera necesidad: peluquerías, lavado de coches, balnearios, cultura, ocio… Nada, desde luego, comparable a lo de esas 910342 personas que viven entre nosotros, junto a nosotros, y que ya no disponen de tarjeta sanitaria. Vinieron en busca de una vida digna… Pero no podemos permitírselo porque tenemos que seguir inyectando dinero a entidades bancarias que son muy, muy españolas.

Será eso lo que llaman la Marca España, ¿no? Y esta marca, ¿está avalada por algún certificado ISO? ¿O somos tan guays que no lo necesitamos para presumir de ella allende nuestras fronteras?

Habría que plantearse regular de alguna forma o establecer alguna medida de normalización y estandarización del estado del bienestar…Claro, que al paso que vamos, la Organización Internacional de Normalización (ISO) nos va a otorgar un rábano. Sí, he dicho rábano, estamos en horario infantil.

Vamos a hablar de eso, digo. No de los que nos gobiernan que no atienden a ningún reglamento internacional, ni siquiera a su propio programa electoral, sino de las medidas de normalización y estandarización y su importancia en nuestras vidas. De paso, les contaré una historia sobre una medida un tanto especial que me descubrió mi amado esposo paseando por el Puente de Harvard sobre el río Charles.

En cuanto a lo primero, es evidente que necesitamos tener medidas estándares, por ejemplo, cuando pensamos en tornillos, tuercas u otro tipo de piezas. En otro caso, sería un desmadre ir a la ferretería con el trasto en cuestión hasta que el dependiente encontrara el tornillo que nos falta, en el trasto quiero decir. Pero no sólo para tornillos…

También la ISO, por ejemplo, tiene una norma, la ISO 16 que establece que una vibración de 440 hercios como estándar de referencia para afinar los instrumentos. Hay quien dice que fue Goebbels (sí, ese Goebbels) el que propuso como estándar la 440 Hz, en lugar de la 432 Hz como se hacía hasta entonces. Pero de esto de Goebbels no he podido encontrar ninguna referencia que me inspire total confianza… En cualquier caso, en Estados Unidos se usaba la 440 desde 1926, antes de que Goebbels fuese ministro, con lo cual, si fue él el que la propuso, parece ser que no hizo más que seguir una corriente que venía desde el otro lado del charco.

Y para el papel. La ISO 216 establece el tamaño de papel y nos permite saber en cualquier lugar que si nos piden un DIN A4, lo que nos están pidiendo es un papel de 21 cm de ancho y 29’7 cm de alto. Ea, aquí no hay error posible. Y no como en otras circunstancias que crees que has pedido un rescate y ni mucho menos, lo que has pedido es un apoyo financiero.

Más cositas… Que si digo 1, eres chico; que si digo 2, eres chica; y si digo 0, no sé cuál es tu sexo. O algo así establece la ISO 5218 para el uso de caracteres que marquen el sexo en estadísticas, por ejemplo.

Hay muchas normas ISO que nos hacen la vida más fácil, las podéis consultar aquí o en la página web oficial de la organización y abarcan aspectos como estándares en gestión medioambiental, tecnología de la información, gestión de calidad, de riesgos en productos sanitarios, inocuidad en alimentos, calidad del software, roscas de tornillos, magnitudes, unidades de medida…

Nos vamos a quedar con esto último, con las unidades estándares de medidas y con Oliver Reed Smoot Jr ¿Por qué? Porque me ha dado por ahí… No, no exactamente. El señor Smoot fue el presidente de la ISO desde enero de 2003 hasta diciembre de 2004, y anteriormente estuvo al frente de la ANSI que es el instituto estadounidense para fijar estándares en Estados Unidos. O sea, que este señor sabe algo de estandarizar y normalizar. Y su primo además fue premio Nobel de Física en 2006. Ya, no tiene nada que ver, pero seguro que en la familia están muy orgullosos.

Volviendo a Oliver Smoot y a su afición por las magnitudes y medidas, lo que les quería contar es que este señor que acabo presidiendo la ISO, en sus tiempos mozos, en 1958, cuando era alumno del MIT y miembro de una fraternidad, Lambda Chi Alpha, fue usado como unidad de medida para medir ¡el puente de Harvard sobre el río Charles! Al fin y al cabo, el hombre es una medida en sí mismo, o eso se dice por los pasillos del MIT.

Según cuentan, unos alumnos de segundo año en la citada fraternidad, cansados de cruzar el puente de Harvard en los días de frío, decidieron usar al novato Smoot, que además era el más bajito, como unidad de medida para medir la longitud del puente. Supongo que previamente, estos notables estudiantes del prestigioso MIT habían tratado de combatir el frío de Bostón con alguna bebida cuanto menos espirituosa. Dicho y hecho. Oliver Smoot se tumbaba en el suelo y sus compañeros pintaban una marca señalando hasta dónde había llegado con su aproximadamente 1’70 de estatura. Así fueron marcando, 10 smoots, 20 smoots, 30 smoots… 60 smoots, 69 smoots (sí, 69 y no 70, ya digo que eran jovencitos y estudiantes del MIT) y así hasta 364,4 smoots y una oreja, la de Smoot, claro.

Cuando Oliver Smoot ya estaba agotado, eran sus propios compañeros de fraternidad los que lo iban colocando. Y así sigue el puente de Harvard, con las marcas de los Smoots. Aquella travesura se quedó formando parte de la ciudad, quizás como dicen, porque tenía los ingredientes básicos de una broma del MIT (léase como broma nerd): era en cierto sentido, científica y no demasiado vándala. Lo que no sospechaban aquella noche seguramente era que aquel muchacho que se tiraba al suelo como unidad de medida acabaría siendo, como ya hemos dicho, presidente de la Organización Internacional de Normalización.

Pero no sólo el puente, los estudiantes del MIT se entrenan para la Marathon de Boston, de 24777 smoots, utilizando es unidad de medida. Como diría Guille, el hermano de Mafalda, «a mí a nerd no me ganáz».

Eso sí, les alabo el hecho de que sus travesuras consistan en mediciones científicas y no en descabezar estatuas como otros…

Seguro que se les ocurre algún personaje de la actualidad como unidad de medida de algo…no sé… ¿de la incompetencia? ¿A quién usamos como unidad de medida para la incompetencia?

Almacenado en: Ahora que los niños salieron a jugar...
3 comentarios

Las Matemáticas son para el verano

30 de julio de 2012

Nos vamos de vacaciones, sí, todo el mes de Agosto. Ésta es, por lo tanto, la última entrada en este blog hasta el mes de Septiembre. No, que no cunda el pánico, quedan muchas matemáticas en la red y siempre podéis repasar vuestras entradas de Mati, una profesora muy particular favoritas…

Pero antes de irnos de vacaciones y suponiendo que estáis leyendo esto porque os atraen las matemáticas (gracias por la parte que me toca 😉 ), hemos decidido en esta entrada recomendar algunos blogs de Matemáticas que, si no conocéis, os servirán para seguir descubriendo y disfrutando de esta disciplina de suprema belleza.

Bueno, antes de hablar de blogs de otros autores, permitidme que os hable de nuestro otro blog, Mati y sus mateaventuras, que fue, al resultar ganador de los premios 20Blogs, el que nos trajo hasta esta ventana de 20minutos. En Mati y sus mateventuras podréis encontrar cuentos para niños (y no tan niños) en los que se exploran temas matemáticos, a distintos niveles. Desde que cumpliera un año, hemos decidido ampliar horizontes y ahora tambień tenemos entradas de Física y Astronomía, gracias a la colaboración de los autores de los blogs Cuentos Cuánticos y Los Pilares de La Ciencia… ¡hasta hemos dedicado una mateaventura a explicar el bosón de Higgs!

Ahora sí, voy a empezar por mi blog favorito de matemáticas (espero que nadie se enfade por esto): Gaussianos. En cierto sentido, es uno de los responsables de que yo esté escribiendo ahora estas líneas. Fue uno de los primero que descubrí y me fascinó, y me fascina, la capacidad de su autor para divulgar matemáticas a distintos niveles. En Gaussianos podéis encontrar de todo, desde citas, anécdotas, chistes, vídeos, historia de las matemáticas, retos (unos más fáciles, otros no tantos) hasta demostraciones elegantes y brillantes de resultados conocidos. En una conferencia que el autor dio en la Universidad de Sevilla le regañé, cariñosamente, por no incluir en su blog temas de Geometría Computacional, área en la que centro mi investigación y ^DiAmOnD^ se arriesgó y me invitó a contar de qué iba eso en esta colaboración, os la dejo por si os mata la curiosidad…

Otro bloguero incansable en la tarea de hacer llegar las matemáticas a cada vez más personas y mostrarles su belleza es nuestro amigo Tito Eliatron. En su casa podéis encontrar todo lo que Tito encuentra por el mundo, tanto el 1.0 como el 2.0, que están llenas de matemáticas y nos las explica claritas y con un toque de humor, ¿por qué no? Una de mis entradas favoritas de este año ha sido ésta

Soy matemático porque no veo árboles ni nubes, veo fractales.

Tito eliatron

Y no sólo en su blog, también Tito Eliatron es el motor del Carnaval de Matemáticas. Desde la página del Carnaval podréis acceder a casi todos los blogs en habla hispana que dedican sus entradas a la divulgación de esta disciplina. Y si os animáis, podéis participar escribiendo sobre mates en vuestros blogs 🙂

Pero si tu interés por las matemáticas está incrementado por el hecho de que eres profesor de la materia no debes perderte el blog de Matemáticas interactivas y manipulativas. Sí, yo también querría que ellos fueran los profesores de mis hijos, lástima que el señor Wert y otros como él no vean estos trabajos de los profesores de la enseñanza pública…

Más profesores de nuestra enseñanza pública que nos ayudan a la difusión de la disciplina: Los matemáticos nos son gente seria, Matemático en el instituto, Tocamates, Algo más que números… son muchos los profesionales del área que dedican parte de su tiempo libre a divulgar y ayudar a otros compañeros y/o las familias. Podéis encontrar muchos más, como he mencionado, a partir de la página del Carnaval o de su perfil en Facebook. También en este apartado os recomiendo el blog de Sangakoo.

Y si lo que os apetece es ver cómo la matemática se convierte en arte, no podéis perderos Juegos topológicos, el canal de vídeo de George Hart o el blog de su hija, Vi Hart.

Seguro que olvido algún blog interesante, pero es lo que tiene el calor, que nos atonta, aún más… Así que os voy a pedir un favor, si detectáis una ausencia imperdonable en la lista, por favor, dejadnos el enlace en los comentarios ¡Gracias!

Y nada más, por ahora. Volvemos en Septiembre. Esperamos que nos echéis tanto de menos que esteis por aquí, ansiosos, esperando más mates 😉

Almacenado en: Ahora que los niños salieron a jugar...
8 comentarios

Hemos usado la media por encima de nuestras posibilidades

23 de julio de 2012

Últimamente estamos siendo bombardeados, con datos por ahora. Cifras de paro, de dinero que desaparece bajo la atenta mirada incluso de miembros de nuestra realeza o de nuestros mejores ex-ministros de Economía, impuestos que suben, sueldos que bajan, recortes en sanidad, educación, ciencia… No me río más en estos días porque no soy diputada del PP…

Pues bien, ante casi cualquier ocasión que se manejen datos, alguien acaba realizando la media aritmética de dichos datos para dar una información relevante acerca de ellos. Sin embargo, en muchas ocasiones, la media aritmética no es adecuada en absoluto. Voy a dar algunos ejemplos reales como la vida misma.

He asistido a varias reuniones en las que el director de una escuela técnica argumentaba que la carrera que en ella se impartía no era de tres años sino de ocho porque esa es la media de lo que tardaban los alumnos en terminarla. Al margen de que no acabo de entender por qué se tenía que vanagloriar de las dificultades que se encontraban los alumnos en su centro, nunca le he visto yo la gracia a este tipo de cosas, resulta que estaba utilizando la media para algo que no es relevante en absoluto. Se puede ver con un ejemplo muy simple (y algo simplista). Si 5 alumnos terminan sus estudios de esa carrera en 3, 4, 4, 4 y 20 años (este último igual los abandonó durante un tiempo o se dedicó a ellos con poco interés por las razones que sean), resulta que la media entre los 5 es de 7 años. Pero este dato es poco representativo ya que todos salvo uno terminaron sus estudios en 4 años o menos. En este caso, sería mucho más descriptivo (estamos hablando de una disciplina llamada Estadística Descriptiva) utilizar la mediana (o percentil 50) que es el valor central de todos los valores que tenemos, con lo cual no influye nada que el que más tarde sea 10, 20 o 50 años. En nuestros ejemplo, la mediana, el valor que está en el centro si los ordenamos de menor a mayor, es 4. Así, si la mediana en acabar una carrera es de cuatro años, esto significa que si entran cien alumnos a esa titulación, en cuatro años al menos cincuenta de ellos tendrán terminados sus estudios; por lo menos, todos los anteriores al valor central en esa lista en esa lista. Por ejemplo, si tenemos trece alumnos que tardaron, respectivamente, los años que aparecen en la lista siguiente ordenados de menor a mayor

3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 7, 20, 30

Si calculamos la media aritmética de los datos anteriores tendríamos que la media para finalizar estudios es de 7 años, mientras que la mediana, que sería el valor en la posición 7 (el central) es de 4 años. Creo que queda claro que la segunda medida es más descriptiva puesto que 10 de los estudiantes finalizaron sus estudios en 4 años o menos, ¿no?

El error anterior es porque se suele confundir media con valor central en muchas ocasiones, sin considerar cuántos elementos están por encima de la media (o cuántos por debajo). Por ejemplo, la media de piernas en la humanidad, el número de piernas por humano, es estrictamente inferior a 2. Por lo tanto, ¿podemos considerar una anomalía que todos los miembros de mi familia estén por encima de la media en número de piernas? Evidentemente no, es más, en este ejemplo se suele considerar como nada deseable estar por debajo de la media y absolutamente normal estar por encima de la media.

Pero existen otros malos usos de la media aritmética que son más preocupantes porque producen resultados totalmente erróneos. Un ejemplo muy simple sobre subida de precios: supongamos que en 3 años los precios de cierto producto han subido un 10%, un 20% y un 30% ¿Cuánto han subido en promedio? Todos entendemos que en promedio se refiere a qué mismo porcentaje tendría que haber subido cada año (cada año el mismo porcentaje) para obtener al cabo de los tres años el mismo precio. Obsérvese que para obtener el precio del primer año (tras una subida del 10%), tenemos que multiplicar por 1,1 el precio inicial. Al precio así obtenido tenemos que multiplicarlo por 1,2 (subida del 20%) para obtener el precio tras el segundo año. Y a dicho precio hemos de multiplicarlo por 1,3 (subida del 30%) para obtener el precio final. Así si el precio inicial es 100, el resultado final será:

100 x (1,1) x (1,2) x (1,3) = 171,6

Sin embargo, si consideramos la media aritmética de 10%, 20% y 30% (o de 1.1, 1.2 y 1.3) obtenemos un porcentaje del 20% (o multiplicar por 1.2), pero si aplicamos esa subida del 20% cada año, el resultado que obtenemos será:

100 x (1,2) x (1,2) x (1,2) = 172,8

Así que no tiene sentido proporcionar la media aritmética para calcular la subida anual promediada de los precios de un artículo. En este caso tendríamos que haber calculado la media geométrica de los tres números 1.1, 1.2 y 1,3 (la media geométrica de dos número es la raíz cuadrada del producto de dichos números, de tres números la raíz cúbica del producto, de cuatro números la raíz cuarta del producto y así sucesivamente). La raíz cúbica del producto de esos tres números es 1,19721577

Efectivamente si aplicamos cada año una subida del 19,721577 % obtenemos:

100 x (1,19721577) x (1,19721577) x (1,19721577) =171,6

que es el resultado correcto.

Espero haberos convencido de que la media no es siempre una medida representativa de los datos que estamos analizando. Hemos visto dos medidas que son mejores en según qué situaciones, la mediana o la media geométrica.

Siempre, claro está, que queramos ser fieles a la verdad y dar información lo más cercana posible a la realidad, porque lo creáis o no, hay gente que sigue tratando de manipularnos por encima de sus posibilidades…

Tags: Estadística Descriptiva, Media aritmética, Media geométrica, Mediana | Almacenado en: Ahora que los niños salieron a jugar...
Comentarios desactivados en Hemos usado la media por encima de nuestras posibilidades

Julio es un buen mes para una revolución…

16 de julio de 2012

La libertad guiando al pueblo en Julio de 1830

Había una vez un gobierno absolutista que gobernaba sólo para los más ricos y para el clero; un rey Borbón que insultaba constantemente a los demócratas de su país; leyes que indemnizaban a los ricos por sus pérdidas pero que iban condenando al pueblo a perder lo que habían conseguido: libertad, igualdad…ya saben…

Cuentan que un consejo de ministros, presidido por el Borbón, aprobó en julio una serie de decretos que afianzaban la crueldad del gobierno… Cuentan que el pueblo se cansó, encolerizó viendo como unos pocos, muy pocos comparados con ellos, intentaban abolir y suprimir todo su bienestar social… Cuentan que aquel mes de julio hubo una gran revolución…

Efectivamente, hablo de la Revolución de Julio. Fue en Francia y fue en 1830. Eran otros tiempos…

La libertad, ese ruiseñor con voz de gigante, despierta a los que duermen más profundamente… ¿Cómo es posible pensar hoy en algo, excepto en luchar por ella? Quienes no pueden amar a la humanidad todavía pueden, sin embargo, ser grandes como tiranos. Pero ¿cómo puede uno ser indiferente?

Ludwig Boerne, 14 de febrero de 1831

¿Que por qué me acuerdo hoy de esto? Pues está claro, porque entre los revolucionarios de aquel mes de Julio tan lejano estaba Évariste Galois, matemático francés que a pesar de su corta vida, murió a los 20 años, dejó tras de sí una contribución fundamental en varias ramas de las Matemáticas: la Teoría de Galois ¿Qué otra cosa si no me iba a recordar una revolución en pleno mes de julio?

Aunque no se conocen con exactitud los detalles que rodean la muerte de Galois, parece que no murió por su carácter rebelde, antieclesiástico y antimonárquico. No. Eso le sirvió para ser expulsado de la École Normale Supérieure y para pasar unos mesesitos a la sombra. Galois murió en un duelo, todo muy romántico como corresponde a un buen matemático, al que asistió una mañana de mayo de 1832, sabiendo que iba a morir, puesto que, según parece, enfrente estaría un oficial, republicano como él, con fama de ser un gran tirador. Pobre Évariste… ¿Fue un duelo por amor? Tampoco se puede afirmar con rotundidad porque aquella noche, consciente de que era su última noche, Galois escribió tres cartas. En una de ellas, a dos amigos suyos:

París, 29 de mayo de 1832

Mis buenos amigos,

He sido provocado por dos patriotas. … Me ha sido imposible rehusarme. Les pido perdón por no haberles advertido a ninguno de ustedes. Pero mis adversarios me hicieron prometer por mi honor el no prevenir a ningún patriota. Su tarea es muy simple: demostrar que me he batido a pesar de mí es decir, después de haber agotado todos los medios que cabían, y decir si soy capaz de mentir, mentir, incluso por las cosas más triviales.

Guarden mi recuerdo, ya que la suerte no me ha dado suficiente vida para que la patria sepa mi nombre.

Muero, su amigo,

E. GALOIS

Esto podría inducir a pensar que fueron motivos simplemente políticos los que llevaron al joven matemático francés aquella mañana al estanque cercano a la Rue de la Glacière a encontrar la muerte. Pero en otra de las cartas que escribió, ésta a sus compañeros republicanos, el joven Galois decía:

París, 29 de mayo de 1832

Ruego a los patriotas, amigos míos no me reprochen por morir de otra manera que por el país. Muero víctima de una infame coqueta y dos incautos. Es dentro de una calumnia insignificante que se extingue mi vida.

¡Oh! ¡Por qué morir por tan poca cosa, morir por algo tan despreciable!

Pongo al cielo por testigo de que fue constreñido y forzado que cedí a una provocación que traté de evitar por todos los medios.

Me arrepiento de haber dicho una verdad odiosa a hombres tan poco capaces de escucharla con serenidad.

Pero al final dije la verdad. Llevo a la tumba una conciencia libre de mentira, libre de sangre patriota.

Me hubiera gustado dar mi vida por el bien público.

Perdón para aquellos que me mataron, son de buena fe.

E. Galois

Esa infame coqueta, según se ha podido descubrir a partir de unas cartas encontradas a Galois, pudo ser Stéphanie-Félicie Poterin du Motel, hija del médico que regentaba la pensión en la que se alojaba nuestro protagonista. Hay quien señala que ella tenía novio y que fue su novio el oficial que acabó con la vida de Évariste…¿quién sabe? No es pequeña la controversia alrededor de la muerte de este matemático rebelde y romántico.

Pero había una tercera carta que es la responsable de que hoy estemos hablando de Évariste Galois, la carta que escribió a Will-Auguste Chevalier, pidiéndole que mostrase sus trabajos a Gauss y Jacobi, los únicos matemáticos que según Galois podrían entenderlos, una carta testamento que daría lugar a la Teoría de Galois.

Vamos a intentar explicar algo de este trabajo.

Resolver ecuaciones ha sido y es fundamental para todas las ciencias o tecnologías. Todos los estudiantes se enfrentan a las ecuaciones de primer grado y, posteriormente, a las de segundo grado. Y todos han de saber que las soluciones de la ecuación (de segundo grado) se expresan en la fórmula:

¿Y si en vez de una ecuación de segundo grado tratamos de resolver una ecuación de tercer, de cuarto grado? Pues desde el siglo XVI se conocen soluciones a este tipo de ecuaciones (naturalmente necesitan, en su expresión raíces cúbicas o cuartas).

Aquí una pequeña digresión: en un libro muy recomendable A history of pi de Petr Beckmann (ignoro si existe traducción al castellano) se cuenta que cincuenta años antes de que el italiano Cardano publicara la solución a la ecuación de cuarto grado en 1545, un español Pablo (o Paolo) Valmes había encontrado dicha solución y por ello fue condenado a morir en la hoguera por el Inquisidor General Tomás de Torquemada ya que:

Es el deseo de Dios que esa solución sea inaccesible al entendimiento humano.

Bien es verdad que dicha historia no ha podido ser corroborada por otros investigadores, por lo que la dejaremos sólo en una curiosa (y representativa) leyenda. Volvamos a las ecuaciones, que me despisto y me enfado…

Como ya se ha dicho, se sabía cómo resolver las ecuaciones hasta grado cuarto desde el siglo XVI, pero las de grado cinco o superior se resistían. Hasta 1824, en este año, Abel demostró que existen ecuaciones de grado mayor o igual a cinco que no se podían resolver mediante una fórmula que envolviera a los coeficientes de la ecuación ligados por operaciones algebraicas como suma, producto, división o raíces (de cualquier grado), lo que técnicamente se conoce resolver una ecuación por radicales. Sin embargo, otras ecuaciones sí que podían ser resueltas por ese método. Aquí es donde aparece la teoría de Galois que consigue, entre otras cosas, determinar exactamente qué ecuaciones pueden ser resueltas por radicales.

Dentro de la teoría de ecuaciones, he investigado bajo qué condiciones las ecuaciones son resolubles por radicales: esto me ha da dado la ocasión de profundizar esta teoría y de describir todas las transformaciones sobre una ecuación, aún si no es soluble por radicales.

Carta de E. Galois a su amigo Chevalier

Se refiere a otros radicales, no a los jóvenes que como él se revelaban contra la autoridad ante la injusticia…

Pero la teoría de Galois también puede ser utilizada para determinar qué construcciones pueden ser llevadas a cabo con regla y compás: un problema de geometría que se remonta a la Grecia clásica. Por ejemplo, con la teoría de Galois se puede probar que el problema de la trisección del ángulo (dividir un ángulo cualquiera en tres ángulos iguales) no puede resolverse usando sólo regla y compás.

De mis tiempos de estudiante en la facultad de Matemáticas recuerdo el comentario jocoso, y con mucha mala leche, de «menos mal que lo mataron, si no, no aprobaríamos nunca la teoría de grupos» Evidentemente, entonces y ahora, lamento la muerte de este ilustre matemático que con 20 años ya fue capaz de elaborar toda una teoría con tanta trascendencia en las Matemáticas, la Física, la Informática… Pero también en estos días, no puedo evitar añorar el espíritu revolucionario y la valentía de aquel estudiante que participó activamente en la revolución de su pueblo contra un gobierno de unos pocos que les oprimía y que cuando estaba a punto de morir, tras el citado duelo, dijo a su hermano Alfred:

No llores, necesito de todo mi coraje para morir a los veinte años.

En fin… como también escribió Évariste la noche antes de morir:

Después de esto habrá, espero, gentes que encontrarán provechoso descifrar todo este lío.

Él hablaba de ecuaciones…

Tags: ecuaciones, Ecuaciones algebraicas, Évariste Galois, Teoría de Galois | Almacenado en: Ahora que los niños salieron a jugar...
9 comentarios

¿Dónde estabas y qué hacías cuando anunciaron que habían encontrado el Higgs?

09 de julio de 2012

Pues sí. Entre tanta mala noticia y el desánimo general, estos días hemos tenido la suerte de ser testigos de uno de los acontecimientos científicos más importantes de los últimos tiempos: los portavoces de los experimentos ATLAS y CMS anunciaban el descubrimiento de una nueva partícula compatible con el buscado bosón de Higgs, con una probabilidad del 99,999994%

I think we have it

Rolf Heuer

Peter Higgs

Que sí, que no es 100% pero la comunidad científica lo considera como certeza, y no como otras comunidades que aceptan la existencia de otras cosas casi sin… bueno, que me desvío…

El caso es que unidos a la muerte de JFK, el alunizaje del Apolo 11, nuestro 23 F, el ataque a las Torres Gemelas o incluso nuestra flamante copa del mundo de fútbol, puede que alguien nos pregunte también:

«¿Dónde estabas y qué hacías cuando anunciaron que habían encontrado el Higgs?»

Sobre Higgs y su partícula se han escrito estos días miles y miles de líneas, como era de esperar ante tamaño acontecimiento. Por esa razón y porque no soy experta en el tema, esta entrada no va sobre el experimento del Laboratorio Europeo de Físca de Partículas (CERN). Pero entre todas las informaciones, reacciones y comentarios que hemos podido escuchar estos días, no faltan los que apuntan a Peter Higgs como futuro premio Nobel de Física, entre ellos Stephen Hawking. Ya nos enteraremos…

Lo que es seguro es que a mí nunca me darán el Nobel de Matemáticas por varias razones. Una de ellas es porque no existe el premio Nobel de Matemáticas.

Recuerdo cuando era jovencita, un poco más joven que ahora, y mi profesor de Análisis de Variable Compleja en 4º curso de Matemáticas nos presentaba el teorema de Mittag-Leffler sobre funciones meromorfas, polos y tal. No os voy a contar el teorema, tranquilos, pero tras enunciar el citado resultado en la pizarra, nuestro profesor se dirigió a nosotros y nos dijo «Por culpa de este señor, no me dieron el premio Nobel de Matemáticas». Yo me quedé muy apenada, tengo que reconocer que sentía cierta debilidad por mi profesor de variable compleja y que era (y sigo siendo) bastante ingenua y despistada. Fue entonces cuando nos contó lo que luego descubrí que era una leyenda urbana muy conocida: que Gösta Mittag-Leffler había molestado a Alfred Nobel teniendo algo que ver con la mujer del segundo.

Alfred Nobel

Eso es falso también por varias razones, la primera porque Nobel nunca se casó. Su amor más duradero (18 años) fue Sophie Hess, pero no hay evidencias de que ella y Mittag-Leffler se llegaran a conocer. Y hablando de amores de Don Alfred, también hay quien apunta que fue otro de los amores de su vida, Bertha von Suttner el que lo inspiró a dotar un premio Nobel para la Paz. De hecho, fue la primera muer que consiguió tal galardón.

Pero volvamos a las Matemáticas, si no fue por asuntos amorosos, ¿por qué Nobel no incluyó un premio para esta disciplina? Muchas son las teorías y algunas de ellas siguen señalando a Mittag Leffler como responsable. Aunque es poco probable que estos dos caballeros interactuaran mucho, puesto que Nobel emigró de Suecia en 1865 y en esa época Mittag Leffler era un estudiante, hay quien señala que hubo alguno enfrentamientos entre ellos, por ejemplo, cuando el matemático propuso a la matemática Sofia Kovalévskaya como profesora de la Universidad de Estocolmo y Nobel se negó. A pesar de eso, Kovalévskaya lo consiguió convirtiéndose, así, en la primera mujer europea que conseguía una plaza de profesora universitaria en Europa aportando importantes contribuciones en Análisis, Ecuaciones Diferenciales y Mecánica. Yo no quiero malmeter… todo esto son conjeturas… pero de nuevo hay una mujer por medio…hay que reconocer que Mittag Leffler era muy guapetón.

Tonterías aparte, sea por lo que fuera, son muchos los que apuntan sobre la supuesta animadversión de Nobel hacia este matemático sueco hasta el punto de conjeturar que no quiso crear el premio Nobel de Matemáticas para no tener que entregárselo a Mittag Leffler que era un seguro candidato, pero los que sugieren esto olvidan que por aquella época Poincaré o Hilbert tampoco eran malos para el premio, los muchachos…

Magnus Goesta Mittag-Leffler

No falta la hipótesis de que, simplemente, a Alfred Nobel no le interesaban las Matemáticas, que estaba más interesado en premiar a descubrimientos importantes que promovieran el desarrollo y que, en este sentido, esta disciplina le pareciese demasiado teórica. Por si alguien en este punto tiene la tentación de cabecear dándole la razón a Don Alfred, le recomiendo que lea esta entrada sobre para qué sirven las matemáticas.

Tampoco hay que perder de vista que en aquella época, Mittag Leffler había conseguido que el rey Óscar II de Suecia y Noruega, del que se conocía su debilidad por las matemáticas tras su paso por la Universidad de Uppsala, otorgase un premio de una medalla de oro y 2500 coronas al ganador de un concurso matemático propuesto por Mittag Leffler, con ayuda de colegas como Hermite y Weierstrass. Aunque la dotación del premio no era muy grande, el hecho de que fuese otorgado por un rey podría haber cohibido a Nobel al no querer competir en la misma categoría con aquellos premios, ¿quién sabe?

Como se suele decir, el uno por el otro y la casa sin barrer… El caso es que no existe el premio Nobel de Matemáticas. Eso sí, las mentes maś brillantes y destacadas en este área pueden optar a otros premios como la Medalla Fields o el Premio Abel otorgado también por el rey de Noruega. Pero si me permitís el chiste malo y fácil y parafraseando a su compatriota Stieg Larsson, al señor Nobel, con todos mis respectos y desde el cariño, yo le llamo «El hombre que no amaba a las Matemáticas»

Nota 1: Para mentes frikis, el teorema de Mittag-Leffler tiene una aplicación práctica a la hora de cazar leones en el Sahara. A saber:

El número de leones en el desierto del Sahara es finito, así que tal conjunto no tiene puntos de acumulación. Utilice el teorema de Mittag-Leffler para construir una función meromorfa con un polo en cada león. Al ser un animal tropical, se congelará si se coloca en el polo, y entonces podrá ser fácilmente capturado.

Patricia Dudley, G.T.Evans, K.D.Hansen, I.D. Richardson; American Mathematical Monthly, 75, 1968, pp. 896-897

Otro día os cuento otros teoremas relevantes para cazar leones en el Sáhara.

Nota 2: Como he dicho al principio, hay mucha información sobre el descubrimiento de la partícula de Higgs, enlazo algunas entradas asequibles para todos:

Nota 3: Respondiendo a la pregunta que da título a esta entrada, me siento afortunada de haber tenido aquel día invitado en nuestro Departamento al Dr. Enrique Fernández Borja del Instituto de Gravedad Cuántica de la Universidad de Erlangen-Nuremberg, autor además del blog de divulgación Cuentos Cuánticos, al que agradezco su paciencia y la claridad de sus explicaciones respondiendo mis preguntas.

Tags: Alfred Nobel, Higgs, Medalla Fields, Mittag-Leffler, Premio Abel, Premios Nobel | Almacenado en: Ahora que los niños salieron a jugar...
16 comentarios

Paseando por la Gran Manzana (sin Euclides de la mano)

02 de julio de 2012

En capítulos anteriores vimos cómo la distancia más corta entre dos puntos de la superficie terrestre no siempre es lo que parece. Así, la distancia más corta entre Sevilla y la capital de las Islas Salomón viene dada por esta curva:

Pero, ¿es ese un fenómeno que se da sólo porque la esfera no es plana? ¿si nos restringimos a porciones más pequeñas de la Tierra, como ciudades, que son casi un plano, podemos considerar que la línea recta es la distancia más corta entre dos puntos? Bueno, la verdad es que no del todo puesto que otras consideraciones aparecen en este caso. Así que tratemos de fijar conceptos:

Supongamos que estamos en una gran ciudad y queremos llegar de un punto a otro, ¿consideraremos la recta como el camino óptimo? Si se puede ir en línea recta sí, pero, en general la línea recta entre dos puntos en una ciudad implica atravesar edificios lo cual puede traer inconvenientes que no ha lugar considerarlos aquí. Entonces me parece que no es mala idea buscar la distancia más cortas en una ciudad «andando por las calles» (el problema de circular es ligeramente más complicado puesto que implica direcciones únicas). como paradigma de ciudad para este ejemplo se suele tomar es el de la parte central de Manhattan por estar muy bien estructurado.Así supongamos que queremos ir de un punto a otro de Manhattan (con o sin la compañía de Euclides) y que no vamos a atravesar rascacielos porque eso no está bonito, no. ¿Cuál será esa ruta?

Figura 1

En la Geometría Euclideana, que es la geometría que todos aprendemos desde nuestros primeros años de estudios, la distancia entre dos puntos se mide como la longitud del segmento que los une, o dicho de otra forma, como el módulo del vector que esos dos puntos definen. Esa forma de medir la distancia es conocida como distancia euclídea y es la que usamos cuando medimos usando un metro entre los dos extremos de lo que queremos medir. En realidad, se trata de una consecuencia del Teorema de Pitágoras. Si tenemos dos puntos en el plano de coordenadas (a,b) y (c,d) respectivamente y queremos calcular la distancia euclídea entre ellos, basta con fijarse que la longitud de los catetos del triángulo rectángulo que definen son (c-a) la de uno y (d-b) la del otro. Entonces, por el Teorema de Pitágoras, sabemos que la distancia euclídea se mide como

Ahí todo está bien y correcto, pero esa no es la única forma de medir la distancia entre dos puntos en el plano. Existe otra distancia, conocida como Distancia de Manhattan o Distancia L₁, que mediría la distancia entre los puntos de la Figura 1 como

Es decir, la suma de las longitudes de los dos catetos del triángulo rectángulo. O bien, la de cualquier ruta que una al punto (a,b) con el punto (c,d) a través de segmentos horizontales y verticales, en otras palabras, la longitud de cualquier escalera que suba desde (a,b) con el punto (c,d)

En verde, la distancia euclídea, y en rojo, azul y amarillo, la distancia Manhattan: todas ellas son rutas óptimas. (Imagen sacada de aquí)

Pues bien, cuando se trata de diseñar rutas de recorrido mínimos en ciudades, tiene más sentido usar esta distancia que la Euclídea, por lo de no atravesar rascacielos que habíamos dicho. Es más, puesto que todas las ‘escaleras’ tienen la misma longitud, nos permite elegir entre distintas opciones, en función de semáforos, zonas de dudosas seguridad, etc…

Evidentemente, no todas las ciudades, ni siquiera Nueva York, están distribuidas como una cuadrícula, pero se considera para según qué problemas de dieños de rutas este tipo de distancia. Y también, cómo no, en el diseño de circuitos ortogonales en los que predominan la conexiones en vertical y horizontal, o en el de un plano de metro.

Otra cosa que no diríamos si pensáramos con la distancia de Manhattan es “No había nadie en 10 Km a la redonda” Porque cuando utilizamos esta expresión, estamos intrínsecamente midiendo con la distancia euclídea. Con esta distancia, la que usamos habitualmente en el día a día, los puntos que están a menos distancia de 10 Km de nosotros, son aquellos que están contenidos en un círculo alrededor nuestra de radio 10 Km.

Pero si pensáramos con la distancia de Manhattan, no sería un círculo, sino ¡un rombo!

Todos los puntos de la frontera del círculo de la izquierda están a la misma distancia euclídea del origen de coordenadas, y todos los puntos de la frontera del rombo de la izquierda están a la misma distancia L₁ del origen de coordenas, como se explica en la siguiente figura:

El punto verde y el punto rojo están a la misma distancia del punto azul (nótese que el ángulo formado por el rombo y el eje en el punto verde es de 45º y, por lo tanto, la longitud de los dos catetos del triángulo rectángulo formado es la misma, está representada con a en la Figura) Y en general, cualquier punto de la frontera del rombo está a la misma distancia del origen (punto azul).

Ahora vamos a ver, que dependiendo de la distancia elegida, el punto más cercano a uno dado puede ser distinto, lo que sería de utilidad conocer a la hora de diseñar rutas de longitud mínima, por ejemplo, para empresas de distribución, mensajería…

Si usamos la euclídea (la usual) el punto rojo está más cerca del origen (en azul) mientras que si usamos la de Manhattan el origen esá más cerca del punto verde.

Eso sí, puede que la distancia Manhattan sea más práctica y refleje mejor la realidad en el diseño y optimización de rutas de distribución, pero mi experiencia como madre me permite asegurar que cuando somos niños es la distancia eulcídea la que ‘traemos’ instalada: «De aquí para acá, mío, de aquí para allá, tuyo».

Pues bien, ahora que ya conocemos la distancia Manhattan, os formulo una pregunta. Si tenemos dos puntos sobre el plano, P y Q, los puntos que están a la mitad de camino entre P y Q, a la misma distancia de ambos, definen una recta que conocemos, como mediatriz. ¿Y si usamos la distancia L₁,? ¿Qué aspecto tiene la mediatriz entre P y Q?

PS: Cuando explico esta distancia a mis estudiantes no puedo resistir la tentación de llamarla Distancia del Ensanche, y es que Barcelona es mi debilidad (aunque Nueva York no está nada, pero nada mal).

Tags: coordenadas, Distancia, Euclides, Teorema de Pitágoras | Almacenado en: Ahora que los niños salieron a jugar...
5 comentarios

¿Cuál es el camino más corto a las Islas Salomón?

25 de junio de 2012

Imagínense que por alguna razón quieren viajar a las Islas Salomón. No sé, igual conocemos a más gente de allí de la que pensamos, yo qué sé… ¿Cuál creen ustedes que sería la ruta más corta para volar hasta el Aeropuerto Internacional de Guadalcanal, por ejemplo? Puede que alguien tuviese la tentación de tomar el mapamundi y una regla y dibujar la línea recta que une Sevilla, que es de donde yo saldría, con Guadalcanal, por aquello que heredamos de Euclides de que la distancia más corta es una línea recta. Cosa que es cierta si nos movemos en un plano y medimos con la distancia euclídea. Medir con la distancia euclídea no es más que lo que hacemos cuando usamos una regla o una cinta métrica, medir la longitud del segmento que une a los dos puntos en el plano.

Ahora bien, si nos vamos a mover de un punto a otro del planeta, nos estamos moviendo, no sobre un plano, sino sobre una esfera. Ya, ya sé que la tierra no es una esfera, pero se le falta muy poquito, ¿no? Pero venga, vamos a pensar en una esfera, que no tiene por qué ser la Tierra, y vamos a ver cómo se calcula el recorrido más corto entre dos puntos sobre ella.

La línea más corta entre dos puntos de la esfera es la geodésica. «Muy bien, Mati, ¿y qué es una geodésica?» Pues la geodésica que une a dos puntos sobre la esfera, es la curva que se dibuja sobre la esfera si la cortamos con un plano que pase por los dos puntos escogidos y el centro de la esfera. Es decir, que las geodésicas son arcos sobre las esfera, correspondientes a círculos que estarían centrados en el centro de ésta. Vamos, que si pensamos en la esfera terrestre, por ejemplo, los meridianos (que nos permiten medir la longitud) son geodésicas, puesto que son círculos que estarían centrados en el centro de la esfera; mientras que los paralelos (que nos permiten medir la latitud) no lo serán, porque (salvo el ecuador) el círculo que los definen no está centrado en el centro de la esfera.

Antiguamente, era relativamente fácil saber a qué distancia sobre el ecuador (latitud) nos encontrábamos (midiendo la altura del sol o algunas estrellas sobre el horizonte), pero para determinar la posición exacta sobre la Tierra era necesario conocer otra coordenada, normalmente la longitud. El problema de determinar la longitud no se resolvió (gracias al desarrollo de relojes más precisos que los existentes hasta su momento, por parte de John Harrison a mediados del siglo XVIII). Por lo tanto cuando un descubridor se internaba en un océano desconocido como Colón en 1492 se solía seguir no el camino más corto, la geodésica, (para determinarlo sobre la esfera es necesario conocer el punto de partida y el punto de llegada) sino que se navegaba siguiendo algún paralelo. Esto, las corrientes marinas y que no le hicieran caso en Portugal (su primera intención) fue muy importante para el éxito del primer viaje de Colón. Por aquel entonces, la hegemonía de las exploraciones correspondía a la corona portuguesa. Y Portugal había lanzado varias expediciones (Fernão Teles en 1475 y Ferdinand van Olm en 1486).

¿Qué problema encontraron dichas expediciones? Pues que si querían viajar hacia el oeste siguiendo el paralelo y como partían del lugar más lógico para ellos: el punto más occidental dominado por la corona portuguesa: las islas Azores, se encontraban de frente la fortísima corriente del Golfo (y los vientos que la acompañan) lo cual dificultaba tremendamente la navegación y hacía casi imposible avanzar. Colón tuvo la suerte de no ser aceptado por lo portugueses y tuvo que ir a pedir la ayuda a la corona de Castilla, que, al concedérsela, le exigió que debería partir de puerto castellano, por lo tanto, la última tierra conocida que visitaron fueron la islas Canarias (La Gomera y Gran Canaria). Desde las Canarias las corrientes y los vientos apuntan hacia el oeste y permitieron su viaje. De hecho, en el viaje de vuelta la ruta escogida por Colón fue mucho más al norte y así estuvo ayudado por la corriente del golfo que lo empujaba hacia Europa.

Dejando a un lado antiguas rivalidades con nuestros vecinos lusos, que no quiero que nadie piense que estoy haciendo patria ante el inminente encuentro en semifinales de la Eurocopa, y volviendo a nuestros planes de volar a las Islas Salomón, alguien podría caer en la tentación de pensar que la ruta que seguiríamos en el vuelo corresponde con la línea recta que une el origen con el destino con una línea recta sobre el mapa. Pero esto no es así, porque los vuelos de los aviones suelen seguir, salvo algunas restricciones, la ruta marcada por el arco de geodésica que une el aeropuerto de origen con el aeropuerto de destino. Y como veis en la siguiente imagen, en el caso de un vuelo desde Sevilla al aeropuerto internacional de Honiara, la ruta está bastante alejada de esa línea recta.

Imagen creada en http://www.gcmap.com

La diferencia entre la ruta marcada por la geodésica y la que nos proporcionaría la línea recta es más acusada cuanto más largo sea el vuelo y cuanto más diferencia de latitud haya entre los dos puntos. Vean si no, por ejemplo, la geodésica entre Sevilla y París.

Como ya he dicho antes, no es que los aviones sigan exactamente la ruta de la geodésica, porque ésta puede incluir zonas sobre las que no es posible volar por cuestiones geográficas y/o metereológicas, o incluso normativas internacionales de restricciones de tráfico aéreo. Pero no me digan que no les sorprende ver sobre el mapa cuál es la distancia más corta hasta las Islas Salomón… y quién sabe, a lo mejor, tenemos que darnos un paseo por allí.

Tags: esfera, geodésicas, latitud, longitud, meridianos, paralelos | Almacenado en: Ahora que los niños salieron a jugar...
10 comentarios