De nuevo es lunes y de nuevo tenemos que enfrentarnos a una semana marcada por las noticias poco esperanzadoras, aunque eso irá cambiando poco a poco… les quedan pocos medios que controlar. Como estamos todos un poco saturados de esto, os voy a contar un pequeño entretenimiento matemático para que podáis compartir sobre una servilleta a la hora del café.
Para nuestro siguiente truco sólo vamos a necesitar papel cuadriculado y lápiz, o bien dibujar una malla cuadriculada sobre la servilleta en cuestión. Intentaremos que la malla cuadriculada sea lo más uniforme posible, y aceptamos que cada cuadradito tiene área 1. A los cruces entre las líneas horizontales y verticales de la cuadrícula los llamamos nodos.
Ahora vamos a pintar un polígono sobre la malla siguiendo las siguientes reglas:
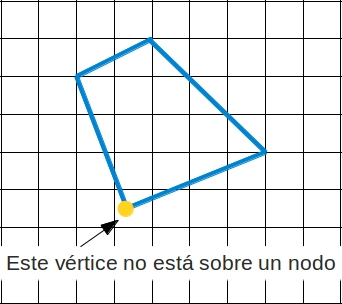
a) Los vértices del polígono deben estar situados sobre nodos de la cuadrícula. El polígono de la figura no es válido, por ejemplo.
b) Debe ser un polígono simple, es decir, que los lados del polígono no se crucen entre ellos, como, por ejemplo en la siguiente figura que representa a un polígono no simple.
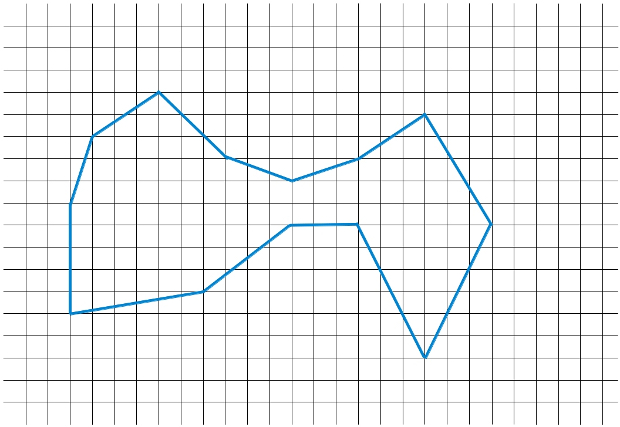
Pues bien, podemos dibujar un polígono como el siguiente:
Atención, pregunta: ¿Cuál es el área del polígono de la figura anterior?
Evidentemente, tenéis la opción de dividir el polígono en otros más simples, triángulos y cuadriláteros, para los que conocéis las fórmulas correspondientes para calcular sus áreas y responder a la pregunta planteada o bien, usar la Fórmula de Pick, que es bastante más rápido.
¿Que cuál es la fórmula de Pick? Claro, se me olvidó ese pequeño detalle… El Teorema de Pick (1899) establece que si tenemos un polígono simple cuyos vértices tienen coordenadas enteras, es decir, cuyos vértices están sobre los nodos de la cuadrícula y llamamos B al número de nodos sobre la frontera del polígono e I al número de nodos de la cuadrícula en el interior del polígono, entonces el área A del polígono se puede calcular con la fórmula:
Vamos a ver que, efectivamente, esta fórmula funciona con polígonos sencillos para los que sabemos calcular sin dificultad el área.
En la siguiente figura, tenemos un rectángulo, de base 4 y altura 6 (os recuerdo que cada cuadradito de nuestra malla tiene área 1), por lo tanto, es un rectángulo de área 24; el triángulo central tiene una base de longitud 8 y una altura de 6, su área es de 24, también; y por último, el cuadrado de la derecha, tiene un lado de longitud 3 lo que nos da un área de 9.
Vamos a calcular sus áreas según la fórmula de Pick, para ello hemos señalado en rojo los nodos de la frontera, los que nos dan el valor de B y en verde, los nodos interiores al polígono, que nos darán el valor de I y… ¡tachán!
En realidad, no hacía falta esta comprobación puesto que el Teorema de Pick está rigurosamente demostrado y publicado en su trabajo Geometrisches zur Zahlenlehre, publicado en Praga en 1899. Lamentablemente, este trabajo de Pick pasó sin pena ni gloria y fue Hugo Steinhaus (al que, por cierto, le dirigió la tesis doctoral nada más y nada menos que Hilbert), el que lo dio a conocer, ya en 1969.
George Pick nació en Viena en 1859, en el seno de una familia judía, lo que sin duda le allanó el camino para poder morir en el campo de concentración de Theresienstadt, unos 60 kilómetros al norte de Praga. Aunque, posiblemente, lo más conocido de los trabajos de Pick, sea la fórmula presentada, llegó a publicar 67 artículos que abarcaban temas tan diversos como el Álgebra lineal, el Análisis funcional, el Cálculo Integral o Geometría, aunque su atención se centraba, principalmente en Funciones de variable compleja, Ecuaciones diferenciales y Geometría diferencial.
Además de lo anterior, a Pick le corresponde el honor de haber introducido al mismísimo Albert Einstein en los trabajos de Cálculo Tensorial de Ricci y Levi-Civita, que sirvieron más tarde a don Albert, en 1915, para formular su teoría de la relatividad general. El propio Einstein escribía en una carta a Levi-Civita:
«Admiro la elegancia de su método de cálculo, debe ser agradable pasear a través de estos campos a lomos del caballo de las matemáticas reales, mientras nosotros tenemos que hacer nuestro camino trabajosamente a pie»
Volviendo a nuestro protagonista de hoy, Pick, parece que él y Einstein fueron grandes amigos, compartiendo además la pasión por la música.
¿Y bien? Volviendo al reto del principio, ¿qué área tiene el polígono grandote que os presenté? Venga, va, os echo una mano por si no os pinta el boli, os coloreo los puntitos 😉







El juego de «unir los puntos» va a tener doble diversión.
La primera lograr la figura más monstruosa que se pueda, y la segunda calcular el área gracias a Pick
Eso si, mente fria. Necesitaremos: un papel cuadriculado, un bolígrafo…..
17 septiembre 2012 | 12:57
O sea, que con estos cálculos se consiguió allanar el camino que llegó a la construcción de la bomba atómica,pues no le veo yo la gracia.
Clica sobre mi nombre
17 septiembre 2012 | 15:14
Muy entretenido http://vivirbienypositivo.blogspot.com/2012/06/sopa-de-capirotadas.html
18 septiembre 2012 | 21:51
Ahora busco mi cuadrícula y mi lapíz a ver si me sale http://goo.gl/fb/cXZSb
18 septiembre 2012 | 21:52