A estas alturas todos sabemos de la publicación en El País de «los papeles de Bárcenas» en los que el supuesto tesorero del supuesto PP llevaba la supuesta contabilidad B del partido (aclaro: la profusión de «supuestos» en la frase anterior es para cubrirme las espaldas, que está el ambiente mu tenso…). Mucho se ha hablado sobre su veracidad o no, pero aquí quiero centrarme en una información aparecida en el diario ABC (¿hace falta que aclare que ABC siempre se ha posicionado en contra de la veracidad de esos papeles?) en los que se afirma que los papeles son falsos desde un punto de vista matemático. Efectivamente, a través de una carta al director de Miguel Lacruz (profesor de la Universidad de Sevilla) se alerta de que los números de «los papeles de Bárcenas» no cumplen la Ley de Benford y que, por tanto, no corresponden a una contabilidad real.
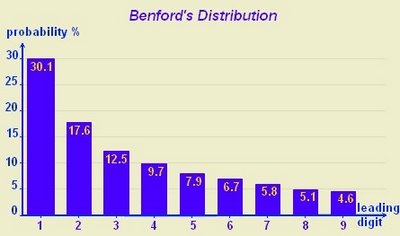
Así, ¿qué es la ley de Benford y qué tiene que decir sobre los papeles de Bárcenas? La ley de Benford la descubrió el astrónomo norteamericano Newcomb al final del siglo XIX; por aquel entonces, en esa era anterior a los ordenadores, se hacía un gran uso de las tablas de logaritmos para realizar cálculos y dicho astrónomo observó que las tablas correspondientes al número 1 estaban mucho más gastadas que el resto, de las que, a su vez, el 2 eran las más deterioradas. Años más tarde, en 1938, el físico Frank Benford observó el mismo fenómeno y recolectó miles de datos provenientes de muy diversas fuentes para elaborar la ley que hoy lleva su nombre. Resumiendo: si tomamos datos que abarquen diversos órdenes de magnitud (esto es: cantidades, si hablamos de euros, entre digamos 100€ y un millón) el primer dígito que más se repite es el 1, después el 2 y así hasta el 9, además, se puede determinar el porcentaje de veces que aparece cada uno y es el dado por la siguiente tabla:
Si los datos de la contabilidad de una empresa se alejan mucho de esta distribución, se puede afirmar que es muy posible que estén maquillados. Es más, se suele afirmar que en los datos maquillados la frecuencia de aparición en primer lugar de cada uno de los dígitos suelen tender a una distribución uniforme: aparecen todos más o menos el mismo número de veces. Pero para ello se han de dar una serie de factores que pueden desvirtuar lo dicho anteriormente: en primer lugar, el número de datos ha de ser suficiente, como todo en estadística, cuantos menos datos se tengan, más fácil es alejarnos de los resultados esperados. En segundo lugar, tal y como se ha dicho, los datos han de tener distintos órdenes de magnitud, esto no sólo implica que tenemos que tener asientos de cantidades que varíen entre los 100 y el millón de euros, sino que tenemos que tener un número suficiente de cada uno de ellos. Por último, existen otros muchos factores que desvirtúan los resultados, en particular una serie de pagos periódicos e idénticos mes tras mes hacen que el primer dígito de dichos pagos aparezca con mayor frecuencia.
En su blog Lacruz da algunos detalles de su «estudio» y afirma que ha recogido solo los asientos desde 2002 hasta 2008, que son relativamente pocos, así ya estamos fallando en el primero de los tres principios expuestos en el párrafo anterior. Es más, aunque hay asientos de varias órdenes de magnitud, la mayoría corresponde a solo dos órdenes: ya hemos fallado también en el segundo de los principios expuestos anteriormente.
En el blog Sintetia, en una magnífica entrada, se hace un estudio más exhaustivo, pero se observa una gran discrepancia en un dígito concreto: el 6. En este gráfico podemos ver en amarillo la distribución del primer dígito en los papeles de Bárcenas y con una marca roja el valor esperado por Benford:
Ya hemos dicho anteriormente que si los datos están maquillados deben aproximarse a la distribución uniforme. Como vemos en el gráfico anterior, dicha distribución está muy alejada de la uniforme y muy próxima a la esperada por la ley de Benford ¿A qué obedece dicho comportamiento anómalo del dígito 6? En la misma entrada de Sintetia se da una respuesta: al cambio de pesetas a euros que hizo que muchos pagos que empezaban por 1 se convirtieran en pagos que empezaban por 6. Se puede ver un gráfico corregido cambiando todo a pesetas:
Ahora el dígito que se «sale» es el 2, pero eso queda explicado por el tercero de los principios que dijimos que desvirtuaban la ley de Benford: la existencia de pagos periódicos (nóminas encubiertas), la mayoría de los cuales, por simple principio igualitario, coinciden y dan la casualidad que empiezan por 2 expresados en pesetas. En este sentido, si miro los movimientos de mi cuenta corriente en el banco, observo que no obedece la ley de Benford ya que los dígitos 1 y 2 se repiten mucho más de lo que predice dicha ley. ¿Se puede deducir que mi cuenta es falsa? Es exigua, pero no falsa, lo que ocurre es que las dos personas que hacemos uso de ella tenemos nóminas que empiezan por 2 y varios pagos (electricidad, etc.) que empiezan por 1 y, para terminar de fastidiar las cosas, cada vez que sacamos dinero del cajero solemos sacar 120€ (reminiscencias de la peseta). En este sentido, es gracioso que en el propio blog de Lacruz se le aplica el mismo test a las cuentas oficiales del PP y salen que también son falsas (por menos).
Entonces ¿qué podemos concluir desde un punto de vista matemático? En primer lugar, que los datos no siguen una distribución uniforme tal y como ocurriría con unos datos inventados, en segundo lugar que se ajustan bastante a los predichos por la ley de Benford salvo cierta cantidad de datos periódicos y constantes que existen por la propia naturaleza del tipo de contabilidad de la que estamos tratando ¿Podemos entonces afirmar que los papeles son ciertos? Tampoco, lo que hemos dicho es que no contradicen necesariamente la ley de Benford.
No, no tenemos nada que decir aquí, dejemos que actúe la Fiscalía Anticorrupción…
Habrá que esperar ahora a ver los papeles del vicepresidente de la CEOE… No podemos quejarnos, que nos tienen bastante entretenidos, ¿verdad?