–¿Nos vamos ya, Sal?
–Un segundo, Ven, me estoy atando las botas…
–Seguro que ya están todos esperando, date prisa, por fi.
–Ya ¿Pero qué haces con la camiseta al revés, Ven?
–No está al revés –respondió el pequeño sin inmutarse –.La etiqueta va por dentro…
–Pero ¡llevas el número en el pecho! –dijo Sal.
–Sí –respondió su hermano tajante.
–Ven, ¡ponte bien la camiseta, estás un poco ridículo! –exclamó el gafotas.
–No me importa, Sal –contestó Ven caminando hacia la puerta ufano –¡Soy un moderno! ¡Esta es la moda!
–Bueno, yo no estoy tan segura… –Mati acababa de llegar, Gauss respiró aliviado.
–¡Hola, Mati! –la saludó el gafotas –. A ver si tú lo puedes convencer…
–Hola, Mati –dijo el moderno –. Ya le he dicho al gafotas que esta es la moda…
–Ya, ya lo escuché –dijo la pelirroja –, y ya te dije que no estaba segura de ello. No creo que sea la forma más frecuente de llevar la camiseta, y en ese caso, no puede ser la moda.
Ven miró a Mati con el ceño fruncido pensando en alguna respuesta lo suficientemente moderna… pero no la encontró.
–La moda –les explicó Mati – es el valor que más se repite en un conjunto de valores o sucesos, por lo tanto, la moda de llevar la camiseta sería con el número en la espalda, que es como la lleva la mayoría de la gente, ¿no, Ven?
–No entiendo nada –se quejó el pequeño.
–Te estoy haciendo un poco de trampa –dijo ella –. Estoy mezclando el concepto de moda de un conjunto de datos en Estadística, con lo que comúnmente llamamos moda en la vida cotidiana, aunque eso sí, están relacionados.
–¿Qué es la moda de la Estadística, Mati? –preguntó inmediatamente el gafotas.
–La moda en Estadística –les contó –es una medida que se utiliza para obtener una primera aproximación de los valores representativos en un experimento, como lo son también la media o la mediana.
Los niños se quedaron muy serios, Gauss miró hacia la ventana disimulando.
–¿Os lo explico con un ejemplo? –les preguntó.
–¡Sí! –respondió Sal inmediatamente y se sentó en el suelo.
–Vale –aceptó el pequeño que estaba un poco despistado.
–A ver –empezó a decir ella –, supongamos que preguntamos el número de calzado que usan todos los niños de tu clase, Ven.
–Tercero A –dijo Ven – ¿Pueden estar también los de tercero B que está mi amigo Pablo?
–Por supuesto –dijo ella –, preguntamos el número de zapato a 40 niños y obtenemos las siguientes respuestas:
–Lo primero que tenemos que hacer –continuó la pelirroja –es ordenar estos datos para poder trabajar mejor con ellos. Para ello, hacemos una tabla donde ponemos cada uno de los valores obtenidos, cada número de zapato, y al lado el número de veces que ha aparecido en la encuesta, la frecuencia.
–Ya podemos saber cuál es la moda de este experimento –anunció Mati –, ¿cuál es el valor que más se repite, el que tiene mayor frecuencia?
–¡32! –gritó Ven de repente.
–Eso significa –añadió ella –que en tu clase la moda es tener un 32 de pie.
–Jo, pues yo no voy a la moda –se quejó el pequeño –porque tengo un 34…
–Bueno –lo consoló Mati –, 34 es un valor bastante frecuente también y cercano a la moda.
–¿Qué pasa si hay varios números de zapatos con la mayor frecuencia, Mati? –preguntó Sal.
–En ese caso –dijo la gafotas –, tendremos varias modas, no pasa nada. Nos quedan la mediana y la media para tratar de estimar el valor central del experimento.
–¿Cómo se calculan la mediana y la media? –preguntó Sal.
–La mediana –dijo ella –es el valor central de todos si los ordenamos de menor a mayor. Nos permite asegurar que es un valor mayor, o igual, que la mitad de los datos, el 50% de ellos, y menor o igual que el otro 50%. Si ordenamos nuestros datos de menor a mayor, como es un número par de datos. 40, tenemos dos valores centrales, en la posición 20 y 21. En ese caso, si hay dos valores centrales, los sumamos y dividimos el resultado por 2. En nuestro experimento, la mediana es 33:
–Eso significa… –masculló el gafotas –que la mitad de los niños tienen un número menor o igual que 33 y la otra mitad, un número mayor o igual que 33, ¿no, Mati?
–Efectivamente, Sal –confirmó esta –, nos da una información de la tendencia central que es, en ocasiones, más representativa que la media.
–¿Cómo se calcula la media, Mati? –preguntó el gafotas.
–Para calcular la media –dijo ella —multiplicamos cada dato por su frecuencia y sumamos todos. Luego dividimos el resultado por el número total de datos, en nuestra encuesta, 40:
–Mira –dijo Ven divertido –, se ha quedado en medio de la mediana y la moda, para que no se enfaden.
–Es cierto –dijo Mati –. Esto ha ocurrido porque nuestra distribución es muy homogénea, no hay datos muy alejados de los demás, ningún niño con un pie enorme o muy, muy pequeñito… Cuando la distribución de valores no es tan homogénea, conviene usar la mediana mejor que la media para dar una estimación central de los datos.
–Pero si salen muy parecidas, Mati… –dijo el gafotas.
–No, no siempre –respondió ella –. Imaginaos que le preguntamos a unos niños por el dinero que le dan en casa cada semana para sus cosas y obtenemos la siguientes respuestas:
–¡Hala! –exclamó Ven –¡Qué suertudos los 2 últimos!
–Bueno, no sé, Ven –respondió Mati –, habrá que ver si además de una buena paga semanal tienen otras cosas más importantes pero… En fin, sigo: si calculamos la media, mediana y moda de esos datos, tenemos que:
–¡Toma. toma, toma! –dijo el pequeño Ven –Ahora sí que no se parecen…
–Ajá –asintió Mati –, esto ocurre porque la muestra de valores no es homogénea. A menudo, hay quien usa el valor de la media para dar una idea de lo habitual en la muestra, pero en este caso, si decimos que los niños suelen recibir 13 euros mensuales, estamos dando una información muy lejana de la realidad, puesto que 11 de los 13 niños, más del 84% de los encuestados, reciben menos de 7 euros…
–Es verdad… –interrumpió Sal.
–Usando la mediana y la moda –continuó la pelirroja –, afirmaríamos que la mitad de los niños reciben 6 euros o menos cada semana y que lo más frecuente es que reciban 5 euros semanales ¿No os parece que da una visión más real de los datos?
–¡Mucho más! –gritó el gafotas –¡Me gusta la mediana!
–A la mediana –añadió Mati sonriendo –se le llama también percentil 50. O segundo cuartil… Pero de este otro tipo de medidas y de otras formas de analizar nuestras muestras de datos hablaremos otro día, que os esperan en la cancha.







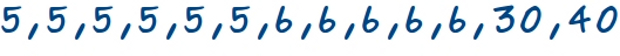

Muy bueno y muy ilustrativo. Da gusto que algo así te saque una buena sonrisa desde por la mañana. Enhorabuena por el blog!!
06 febrero 2013 | 11:04
¡Muchas gracias! No sabes cómo nos gusta tu comentario 🙂
06 febrero 2013 | 11:07
¿Y usted que sabe tanto no sabe como calcular la media de politicos corruptos que hay en este bendito pais? ¡Sería un post muy interesante.
http://www.antoniolarrosa.com
06 febrero 2013 | 14:20
Después de leerte, he decidido Mati,
ser niño nuevamente, coger el arco,
la espada y el puñal de madera,
el capote escondido en la chumbera
o la vieja pelota de trapo y engomada,
y jugar con otros niños en la era.
Esperaré tumbado y con el arco
armado tras los lirios silvestres;
o huiré muy deprisa bajando la ladera,
y saltando el arroyo de juncos flanqueado,
escondiendo el aliento entre los matorrales,
y esperando muy quieto a que el peligro pase.
Si me toca una flecha tendré
que hacerme el muerto y esperar al final,
y quedarme en la arena dibujando figuras,
una recta, una curva, un trapecio quizá;
volveré a ser un niño en busca de aventuras,
mientras las nubes pasan con su lento volar.
06 febrero 2013 | 15:12
Muy ilustrativo, pero dos pequeños errores. En dos ocasiones escribes «…cuando la muestra de valores no es heterogénea…» cuando debería figurar «…no es homogénea»
Saludos
07 febrero 2013 | 20:30
@yomismo
Muchas gracias por el aviso. Ya está corregido.
Un beso
Clara
08 febrero 2013 | 19:23
Profesora, sabes algo de esto?
Dentro de poco secribirá: Alguien sabe si algún día, la sociedad trabajadora la jornada eran 38 horas semanales, tenia extra paga en las horas de trabajo después de la jornada de 8 horas, los festivos eran doble pago y incluso triple, tenían vacaciones pagadas, seguridad social y medicinas, jubilacion a los 60 o 65 años, la vivienda en que vivía la podía pagar con el sueldo que ganaba en 60 mensualidades, etc. etc.
Esta pregunta? Se la podrás hacer dentro de muy poco tiempo a las nuevas generaciones, porque el camino que esta plantando el fascismo y el sistema financiero Internacional, es la demolición de todo lo social pasándolo a ser todo privado manejado por las multinacionales dando unos chochejos de maíz a los trabajdores como se hace con las bestias para que no se muera, a la edad de viejo una inyección letal y a la mierda. Esperamos que en corto plazo venga un salvador que esta en la la tierra y estas bestias corruptas que hoy gobiernan con imposicion satira las fulmine!!!
Conoces en que consistio el «Pacto de la Mocloa», que fue un pacto en los principios de la «democaca» porque lo saben hasta el gatos; Si no lo sabes, preguntaselo a los falangistas que también en esa época, se dividieron, unos eran simples falangistas y otros eran los auténticos.
11 febrero 2013 | 2:08