La hora de las tareas | Mati, una profesora muy particular

Archivo de la categoría ‘La hora de las tareas’

Combina, varía y repite

19 de septiembre de 2012

–¡Gafota no es una palabra del diccionario! –gritó Sal.

–Anda que no –respondió Ven tranquilamente –A ti te llamamos gafotas y te gusta.

–Sí, claro, me gusta –repuso Sal –Pero también podríamos llamarme Picachu y no por eso está en el diccionario… No vale, Ven.

–Pero tú no eres un Picachu –siguió argumentando el pequeño.

–Esa palabra no vale y punto –sentenció el gafotas.

–Eres un mandón, Sal –protestó Ven –Y mandón sí está en el diccionario.

–Busca otra palabra, por favor, Ven –le pidió su hermano tratando de volver a la cordialidad.

–Con estas letras no se puede hacer nada –bufó éste –Son una caca.

–¿Cómo lo sabes? ¿Has probado todas las posibilidades? –Mati acababa de llegar.

–¡Hola, Mati! –saludaron los dos niños y Gauss respiró aliviado.

–Hola, chicos, ¿qué os pasa con el Scrabble?

–Que me han tocado unas letras muy malas –protestó Ven.

–A ver –dijo la pelirroja mirando las letras de su amiguito —a, p, g, a, a, f, a, t, e, o… No están tan mal, puedes construir fogata.

–¡Toma, claro! –se alegró Ven.

–Qué morro, te la ha dicho Mati –protestó Sal sin mucho interés porque estaba dándole vueltas a lo que ella había dicho al llegar –¿Podemos saber cuántas posibles combinaciones hay, Mati?

–Bueno, sí –respondió ella –Pero no todas serán válidas, claro, porque además deben ser palabras que aparezcan en el diccionario.

–¿Cómo se hace? –siguió preguntando el gafotas –¿Como nos enseñaste el otro día? ¿Son combinaciones o variaciones?

–En este caso, serían variaciones, porque es muy importante el orden en el que colocamos las letras, claro.

–No, no se puede… –murmuró Ven pensativo –Hay letras repetidas y el otro día no había equipos repetidos, así qué…

–Efectivamente, cielo –se apresuró a responder Mati –El caso del Scrabble es muy complicado porque además deben estar en el diccionario, pero os puedo enseñar a calcular, si os apetece, a calcular el número de combinaciones y variaciones con repetición.

–¿Nos enseñas? –pidió Sal con los ojos abiertos como platos.

–Con mucho gusto –le respondió ella a la vez que le guiñaba un ojo –Por ejemplo, imaginaos que tenemos 8 caramelos para repartir entre vosotros 2 y Elio…

–No es divisible, Mati –interrumpió Ven.

–Ajá, pero ¿de cuántas formas podemos hacer el reparto? –les preguntó.

–Como a mí me gustan menos los caramelos –propuso Sal –Puedes darle 3 a Elio, 3 a Ven y a mí sólo 2.

–Gracias, Sal –dijo Ven y le zampó un beso.

–Vamos a ir representando las posibles situaciones en el cuaderno –les propuso la gafotas –Ése reparto que propone Sal corresponde con esta elección, por ejemplo, ¿no? El primero para Elio, el segundo para Elio, el tercero para Elio, el cuarto para Sal, el quinto para Sal, el sexto para Ven, el séptimo para Ven y el octavo para Ven.

Los dos hermanitos asintieron con la cabeza.

–Pero ese mismo reparto también corresponde con esta otra elección, ¿veréis? El primero para Sal, el segundo para Ven, el tercero para Elio, el cuarto para Sal, el quinto para Ven, el sexto para Elio, el séptimo para Ven y el octavo para Elio, ¿no?

–¡Toma, claro! –dijo Ven –Sal se sigue quedando sólo con 2 caramelos…

–Eso significa, que son combinaciones, porque no importa el orden en el que elijamos los elementos del conjunto {E,S,V} para formar conjuntos de 8 elementos –les dijo –Pero, en este ejemplo, podemos elegir elementos repetidos, al contrario de lo que pasaba el otro día con los equipos. En este caso, se llaman combinaciones con repetición de 3 elementos tomados de 8 en 8.

–¿Y cuántas son? –preguntó Sal inquieto.

–Dejadme, dejadme que las calcule yo –pidió Ven y se puso a hacer posibles repartos en la libreta de Mati.

Al cabo de un rato, Ven protestó:

–¡Son infinitos, Mati!

–¡Ja,ja,ja! –Mati le acarició el pelo –Son muchos, sí, pero no infinitos, seguro. Os enseñaré la fórmula –Mati escribió en su cuaderno:

–Así que en nuestro caso particular del reparto de caramelos –continuó –Nos quedaría:

–¡Hala, Ven! –dio Sal –Qué exagerado eres… Sólo eran 45… Infinitas dices…

–Pues haberlas hecho tú –le contestó enojado el pequeño.

–Está bien, Ven, no te enfades –respondió Sal –Eran muchas en cualquier caso.

–¡Cómo mola, Mati! –Ven estaba alucinando como siempre.

–Pero, Mati –preguntó Sal –Si se pueden repetir los elementos, nunca importa el orden ,¿no? Sólo importa cuántos de cada uno has cogido, ¿verdad?

–¿Cómo que no? –peguntó Mati cómicamente enfadada –¿Qué pasa con esto?

–¡¡Que este fin de semana han ganado el Sevilla y el Barcelona!! –gritó Ven levantando los brazos –Clara es de Sevilla y Raquel de Barcelona, ¡¡toma, toma, toma!!

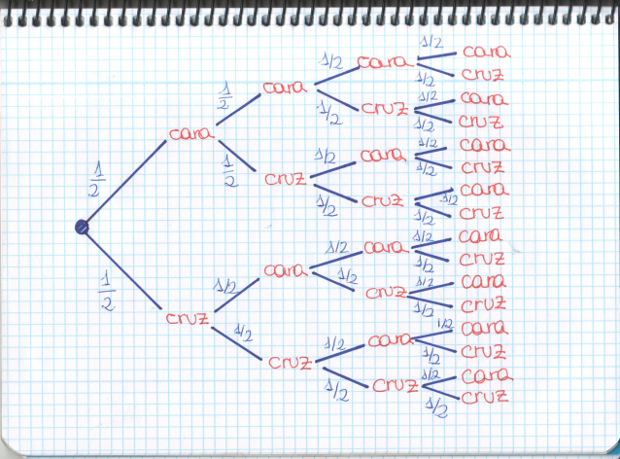
–Eso es, eso es –dijjo Mati divertida –Pero lo que quería que vieseis es que en la quiniela sí importa el orden, no es lo mismo, fijaos si no en estas dos posibles quinielas:

–Aunque tengan el mismo número de 1, de X y de 2 –les dijo –evidentemente, no son la misma, cada signo tiene asignado un partido concreto, se trata de variaciones con repetición, variaciones de 3 elementos (1, X y 2) tomados de 15 en 15.

–¿Cual es la fórmula, Mati? –preguntó Sal un poco ansioso.

–Vamos a verlo –prometió la gafotas y escribió en su cuaderno:

–¡¡Hala!! ¡¡Más de 14 millones de quinielas posibles!! –Ven alucinaba –¡¡Eso sí que es casi infinito!!

–Bueno, Ven –apuntó su hermano –Pero si sabes cuál es el favorito del partido, puedes acertar…

–Eso no sirve, Sal –contestó el pequeño –Ya viste este fin de semana lo que le pasó al …

–Vale, vale –Sal desvió la conversación –¿Y en La primitiva? ¿Qué son? ¿Combinaciones o variaciones, Mati?

–En La primitiva, Sal –respondió la pelirroja –Son combinaciones, no importa el orden en que escojas los 6 números de entre los 49 posibles, sólo qué números escoges…

–Y no se puede repetir, ¿no, Mati? –preguntó Ven.

–No, no se puede repetir –contestó ella.

–Entonces ya lo sé –dijo Sal –Lo explicaste el otro día, 49 sobre 6, el combinatorio ése.

Mati escribió en su cuaderno

–¡Toma, toma, toma! ¡Eso es imposible que te toque! –gritó Ven.

–Imposible, no –contestó Mati –Pero casi… Por cierto, Ven, con esas letras puedes escribir también atafea.

–¿¿Eso qués es, Mati?? –preguntó Sal desconfiado –¿Está en el diccionario?

–No sé, búscalo –dijo Mati con cara de pilla –Voy a salir a dar un paseo con Gauss.

Tags: combinaciones con repetición, combinaciones sin repetición, combinatoria, variaciones con repetición | Almacenado en: La hora de las tareas
1 comentario »

Fútbol y combinatoria

12 de septiembre de 2012

–A ver, Ven, si son 16 equipos, cada equipo jugará 15 partidos… Porque sólo lo haremos a una vuelta, ¿no?

–Claro, pero ¿sólo 15 partidos? Eso son muy pocos, Sal. Acabaremos muy pronto.

–No, no, Ven, pero hay más partidos.

–Ah, claro… Como cada equipo juega 15 partidos y son 16 equipos, tendremos que multiplicar 15 por 16.

–Eso es –corroboró el gafotas mientras su cabecita seguía dando vueltas –creo…

–Haz tú la multiplicación, Sal, que yo todavía no he aprendido…

–A ver, si multiplicamos 16 por 30… –empezó a calcular mentalmente Sal –16 por 3 es, 16 más 16, 32, más 16, 48…Son 480…Ahora me quedo con la mitad, y son 240.

–¡Toma, 240 partidos! –grito el pequeño –Y si hacemos la liga a dos vueltas ¡serán 480!

–Huy, creo que os habéis pasado un poco… –Mati acababa de llegar y Gauss corrió enseguida a su lado.

–¡Hola, Mati! –la saludó Ven alegremente.

–¿No está bien el cálculo, Mati? –preguntó Sal muy concentrado.

–¡Hola, Sal! –dijo ella guiñando un ojo.

–Ah, sí, claro, hola, lo siento –contestó éste.

–No pasa nada, cielo –Mati le acarició el pelo –Y no, no está bien el cálculo.

–¿Por qué? –quiso saber Sal.

–A ver, queréis saber cuánto partidos se van a jugar en una liga con ¿16 equipos?

–Eso, es –afirmó Ven.

–Muy bien –siguió Mati –Una liga con 16 equipos pero sólo a una vuelta, ¿no?

–Ajá… –Ven ponía cara interesante.

–En ese caso –continuó ella –si calculáis 15 por 16, estáis contando 2 veces cada partido, es decir, no hay 240 partidos, sino 120, la mitad.

–No entiendo nada… –terminó aceptando el pequeño.

–Por ejemplo, decidme el nombre de dos equipos de vuestra liga.

—Ven Power –respondió rápidamente Ven.

–Y Sal Athletic —añadió Sal un poco ruborizado.

–Muy bien –siguió la pelirroja —Ven Power jugará 15 partidos, uno de ellos con Sal Athletic, ¿no?

Los niños asintieron con la cabeza, Mati continuó.

–Entonces, el partido entre Ven Power y Sal Athletic ya lo hemos contado. Por lo tanto, cuando contemos los partidos que debe jugar Sal Athletic, serán 14, porque el que juega con Ven Power ya lo hemos contado…

–¡Toma, claro! –interrumpió el pequeño.

–Entonces, ¿cuántos son? –preguntó el gafotas intrigado.

–Pues, exactamente la mitad –dijo ella –Puesto que estás contando cada partido 2 veces, es decir, serían 120 si fuera a una vuelta, y 240 si fuera a dos vueltas.

–Ya, ya lo veo… –Sal seguía pensativo.

–Lo que estáis tratando de calcular es el número de combinaciones o parejas de 2 elementos que se pueden hacer con 16 –les dijo — Si la liga fuera a dos vueltas, lo que queréis calcular es el número de variaciones de 2 elementos en un conjunto de 16.

Los dos niños arrugaron sus caritas y miraron fijamente a Mati.

–Cuando contamos las combinaciones –continuó la gafotas —No importa el orden en que hayamos escogido los miembros de la pareja, es decir, el partido que programamos tomando primero a Ven Power y después a Sal Atheltic es el mismo que si hubiésemos elegido primero a Sal Atheltic y después a Ven Power, ¿no?

Los dos hermanos volvieron a cabecear afirmando.

–Pero cuando queremos contar las variaciones –les dijo —Sí importa el orden, y tendríamos dos partidos diferentes, uno sería Ven Power-Sal Atheltic, en el campo del primero por ejemplo, y el otro sería Sal Atheltic-Ven Power ¿Me explico?

–Te explicas… –dijo Sal.

–Si queréis os enseño unas fórmulas para calcular el número de combinaciones y variaciones que se pueden hacer con un número de elementos…

–¡Sí! –gritaron los dos.

–Estupendo –Mati sonrió –Pero antes de eso, os tengo que enseñar un par de cositas. Primero, qué es el factorial de un número natural…

–Los números naturales son los que sirven para contar… –masculló Ven mientras su hermano lo miraba de reojo por interrumpir a Mati.

–Para calcular el factorial de un número natural –siguió ella –Multiplicamos ese número por todos los anteriores a él hasta llegar al 1. Vamos a calcular por ejemplo el factorial de 5, que se escribe así 5!…

–¡Ja! Como si estuvieras gritando ¡5! –dijo Ven divertido.

–Bueno, pero sólo ponemos el signo de cierre –añadió ella sonriendo mientras escribía en su libreta.

–¿Y el de 8? –preguntó Ven –Como tengo 8 años…

–Vamos a calcularlo… –propuso Mati.

–¡Toma! –se sorprendió el pequeño.

–Sí, los factoriales crecen muy, muy rápido –dijo Mati –Ahora os cuento qué es un número combinatorio –Mati escribió en su cuaderno:

–¿Y eso para qué sirve? –preguntó Ven.

–Pues, por ejemplo, para saber cuántas combinaciones de 2 equipos se pueden hacer con un conjunto de 16, o lo que es lo mismo,

–¡Es verdad! –dijo Sal excitado –¡Me gusta!

–Me alegro –dijo la pelirroja –Pero no sólo sirve para contar el número de pareas posibles, si pensáis en agrupar a los equipos en grupos de 4 como se hace en el mundial, podéis conocer cuántos grupos de 4 equipos diferentes se pueden formar con 4 equipos.

–¿Me dejas intentarlo, Mati? –preguntó el gafotas.

–¡Claro!

–¡Hala! –soltó Ven –Cuántos…

–Ajá –añaddió Mati –Esos son todas las formas posibles de agrupar 4 equipos diferentes elegidos en un grupo de 16.

–Pero Mati –preguntó Sal –¿Cómo se calculan las variaciones si la liga es a 2 vueltas?

–¡Ah, sí! Lo había olvidado –Mati escribió en su cuaderno.

–Es verdad… –Ven alucinaba –Tenías razón.

–Pues sí, chicos, la combinatoria es muy útil para organizar eventos deportivos –dijo Mati y les guiñó un ojo –Y pasa muchas más cosas, claro, otro día os hablo de combinaciones y variaciones con repetición.

–¿Con repetición? –preguntó Sal muy sorprendido.

–Sí, cuando en el conjunto inicial hay elementos repetidos…

–No pueden haber equipos repetidos, Mati –protestó Ven.

–Ya, pero imagina que tenemos en un cajón lleno de monedas, muchas de 5, muchas de 10, muchas de 20 y muchas de 50 céntimos y queremos elegir, por ejemplo, conjuntos de 4 monedas…

–¿¿Cómo se hace?? –preguntó Sal alterado.

–Ya lo he dicho –respondió Mati con sonrisa misteriosa –Os lo cuento en otro momento, ahora vamos a terminar de diseñar esa liga que estabais haciendo.

Tags: combinaciones sin repetición, combinatoria, factorial de un número natural, números combinatorios, variaciones sin repetición | Almacenado en: La hora de las tareas
5 comentarios

¿Y si hacemos bolsas de 7 canicas?

05 de septiembre de 2012

–No, Sal. Es mejor hacerlas de 6, como nos dijo Mati, ¿te acuerdas?

–No, Ven, lo que dijo Mati es que si tenías 6 canicas era más fácil hacer subgrupos que si tenías 5, pero si tenemos 46 canicas no es más fácil con 6 –argumentó el gafotas –Además, nos sobrarían canicas.

–¿Cómo lo sabes? –preguntó el pequeño.

–Porque si divides 46 entre 6, te sobran 4 –respondió Sal.

–¿Es porque 6 y 46 son primos entre sí?

–No, Ven –añadió Sal –No son primos porque los dos se pueden dividir por 2…

–Bueno, qué bien –Mati acababa de llegar –Veo que seguís hablando de números primos, ¿no?

–¡Hola, Mati! –saludó Ven.

–No exactamente, Mati –dijo Sal mientras se ponía de puntillas para dar un beso a Mati –Hablábamos de números primos entre sí. Bueno, en realidad, le explicaba a Ven que no podemos hacer las bolsas con 6 canicas porque tenemos 46 y nos sobrarían canicas.

–Estamos preparando un mercadillo para el domingo, Mati –empezó a contar Ven muy animado–Vamos a vender nuestras canicas, tenemos 46. Mamá nos ha dado bolsitas para que las preparemos.

–Entiendo… -intervino Mati –Esto es un problema de divisibilidad…

–¿De qué? –preguntó el pequeño ven arrugando la nariz.

–De divisibilidad –respondió ella –Tenéis que saber por qué números es divisible 46 para poder hacer las bolsitas sin que sobren canicas.

–Y eso, ¿cómo podemos saberlo? –preguntó Sal intrigado.

–Os voy a enseñar algunas reglas de divisibilidad, ¿queréis?

–¡Sí! –dijeron los dos niños.

–Cualquier número es divisible por 1, así que podríais hacer 46 bolsas de 1 canica…

–¡Toma, claro! –interrumpió Ven –Pero es un rollo…

–Bueno, pues vamos a seguir entonces -Mati le guiñó un ojo —Todos los números pares son divisibles por 2.

–¡46 es par! –gritó Ven.

–Sí, podemos hacer 23 bolsas de 2 canicas –dijo Sal –Pero con 2 canicas, también es muy poca cosa…

–¿Seguimos? –les preguntó Mati —Un número es divisible por 3 si la suma de sus cifras nos da un múltiplo de 3.

–¿46? 4 más 6 es 10…–murmuraba Sal –No, no es divisible porque 10 no es múltiplo de 3.

–¿Cómo lo sabes, Sal? –preguntó su hermano.

–Pues porque si divides 10 entre 3, te sobran –contestó el gafotas.

–Muy bien, chicos –continuó Mati — Ahora, un número es divisible por 4, si sus dos últimas cifras son ceros o múltiplo de 4.

–Las dos últimas cifras de 46 son 46, Mati –dijo Sal –Esta regla es un poco tonta, ¿no?

–Bueno, en este caso, puede –dijo ella –Pero gracias a esa regla sabemos que 5874516 es divisible por 4.

–¡Toma, toma, toma! –exclamó Ven.

–Pues 46 no es divisible por 4 –siguió Sal –Porque 11 por 4 es 44 , así que nos sobrarían 2…

–Efectivamente –continuó Mati —Un número es divisible por 5, si termina en cero o cinco.

–¡Qué fácil! –dijo Ven –No podemos hacer bolsas de 5 canicas.

–No –añadió Sal –Si no queremos que sobren canicas, no…

–Es el turno del 6 –siguió la pelirroja —Un número es divisible por 6, si es divisible por 2 y por 3.

–Pues 46 no es divisible por 6 porque no es divisible por 3 –dijo Ven satisfecho.

–Eso ya te lo dije yo antes… –intervino Sal.

–Vamos con el 7–propuso Mati –Ésta es una de mis reglas de divisibilidad favorita.

–¿Por qué? –preguntaron los dos.

–Ya veréis –anunció la pelirroja con misterio mientras sacaba su libreta.

–¿Qué es eso? –preguntó Ven divertido –¡Es un grafo!

–Sí –dijo Mati –Un grafo que nos va a ayudar a saber si un número es divisible por 7 o no.

–¿¿Cómo?? –Sal estaba cada vez más intrigado.

–Os lo cuento –empezó a decir Mati –Salimos siempre desde el 0, es nuestra posición inicial. Desde allí recorremos tantas flechas azules como indique la primera cifra de nuestro número…

–¡El 4! –dijo Ven –La primera cifra de 46 es el 4.

–Pues empezando en 0 –siguió Mati –Recorremos 4 flechas azules, ¿dónde llegamos?

–Al 4 –respondió Sal.

–Ahora recorremos una flecha roja –les dijo –Y llegamos a 5.

–¿Y ahora? –preguntó el pequeño.

–Ahora, saliendo desde el 5, hacemos lo mismo –les contó –Seguimos tantas flechas azules como indique la segunda cifra, que en nuestro caso es 6.

–Llegamos al 4 otra vez –dijo Sal –¿Ahora flecha roja?

–No, ya no. porque ésta es la última cifra –dijo Mati –Ya hemos acabado, 4 es el resto de dividir 46 por 7, entonces 46 no es divisible por 7.

–¡Toma, toma, toma! ¡Cómo mola! –exclamó Ven.

–¿Y sirve para cualquier número? –preguntó Sal.

–Sí –respondió la gafotas –Siempre. Comienzas en el cero, tantas flechas azules como la primera cifra y flecha roja. Desde donde estás, tantas flechas rojas como la segunda cifra y flecha roja. Y así con todas, excepto con la última cifra, que no usamos la flecha roja después de los azules.

–¡Es chulísimo! –Ven estaba alucinado. Gauss parecía poco preocupado con el asunto.

–Y para el 8, ¿también hay un grafo? –preguntó Sal.

–No –respondió Mati —Un número es divisible por 8, si sus tres últimas cifras son ceros o forman un múltiplo de 8.

–Pero 46 sólo tiene 2 cifras… –afirmó Ven.

–Lo miramos como 046 –les dijo.

–4 más 6 es 10… -murmuraba Sal –No, no es divisible por 8.

–¿Qué pasa con el 9? –quiso saber Ven.

—Un número es divisible por 9, si la suma de sus dígitos nos da múltiplo de 9 –les dijo Mati.

–Pues, vaya, tampoco –se quejó Ven.

—Para que sea divisible por 10, debe terminar en 0 –continuó Mati.

–Tampoco –refunfuñó el pequeño.

–Bueno, Ven –intervino Sal –Las hacemos de 7 y las 4 que sobran, nos la quedamos de recuerdo.

–¡Hecho! –aceptó Ven –¡Somos los más mejores!

Nota de las autoras: El método para conocer el resto al dividir por 7 un número natural lo encontramos aquí y nos encantó 🙂 En su blog, Gaussianos nos cuenta cómo hacer ése grafo para cualquier número natural.

Almacenado en: La hora de las tareas
7 comentarios

Lo primero es lo primero…

25 de julio de 2012

(Fue esta publicación en Google+ la que nos animó a escribir esta entrada, tengo que decir que estupefactas ante las respuestas a la pregunta planteada. No se trata de saber matemáticas, se trata de anumerismo, y el anumerismo también es incultura.)

–Sale 4, Ven.

–Depende Sal, depende de lo cómo lo hagas –respondió el pequeño.

–Pero es que sólo una forma de hacerlo, Ven –repuso el gafotas –Antes que nada, las multiplicaciones y las divisiones…

–Pero, ¿qué divisiones Sal? –se quejó el pequeño –¡No hay ninguna división! Estás obsesionado con las divisiones…

–A ver, chicos, ¿qué os pasa? –intervino Mati.

–Mati, ¿a qué lo primero es multiplicar y dividir?

–Bueno, Sal –dijo la pelirroja –Si no hay ni potencias ni paréntesis…

–¡No hay nada de eso! –Ven estaba enfadándose e hinchando sus carrillos –Ni divisiones…

–En ese caso –intervino Mati sonriendo al pequeño Ven –lo primero que tenemos que hacer es la multiplicación ¿queréis que os preste mi cuaderno para poder llevarnos las operaciones que hacéis?

–Vale –dijo Ven deshinchando sus mofletes y dispuesto a copiar la operación en el cuaderno de Mati –3 por 0 es 0, eso lo sabe cualquiera… Ya sólo queda 7 menos 4… 3. Más 1… 4. Sale 4 Mati.

–Ésta era muy fácil, ¡otra! –gritó Ven muy alegre –¡Ahora con todas las cosas Mati!

–¡Allá vamos! –dijo Mati graciosamente mientras proponía una operación en el cuaderno.

–¡Hala, Mati, te has pasado! –dijo el pequeño.

–¿Qué hacemos primero, Mati? –preguntó Sal ansioso.

–Me alegro de que me hagas esa pregunta Sal –respondió la gafotas haciéndose la interesante –Porque esto me permitirá explicaros la jerarquía de las operaciones.

–¿La qué? –preguntó Ven sorprendido.

–La jerarquía, el orden en el que hay que realizar las operaciones –respondió ella –Vamos a escribirla para que no se nos olvide.

–¿Corchetes? ¿Hay corchetes en las operaciones? –preguntó Ven divertido –Yo creía que sólo había corchetes en la ropa de los bebés…

–No, no son ésos, Ven –dijo Mati –Aparte de los corchetes de la ropa, un corchete puede ser un utensilio de madera con unos dientes de hierro en el que los carpinteros sujetan la pieza que trabajan, o incluso, antiguamente, una especie de policía que detenían a los delincuentes.

–¿Un policía Mati? –Sal parecía sorprendido.

–Sí –confirmo ésta –Siempre me acuerdo de una jácara, un poema gracioso, de nuestro escritor Quevedo que decía

A la sombra de un corchete

vivo en aqueste lugar,

que es para los delincuentes

árbol que puede asombrar

–¿Cómo puede asombrarte un árbol Mati? –Ven parecía desconfiado.

–En esta jácara, el verbo asombrar –dijo Mati con un guiño –se refiere a hacer sombra.

–¡Mola! –dio el pequeño –Asombrar es una palabra polisémica y corchete también.

–Y llave, ¿no, Mati? –añadió el gafotas –Porque esas llaves que aparecen en tu jerarquía junto a los corchetes, no son para abrir puertas, ¿verdad?

–No –contestó ella sonriendo –Las llaves que aparecen en la jerarquía, igual que los corchetes, son signos que se usan para agrupar, como los paréntesis. Pero las llaves y los corchetes cada vez se usan menos para agrupar operaciones…

–¿Cómo son las llaves Mati? –quiso saber Ven –¿y los corchetes?

Mati los dibujó para ellos

–Vamos chicos –propuso la pelirroja –¿Os atrevéis?

–¡Sí! –respondieron al unísono y se pusieron manos a la obra.

–Primero, los paréntesis, Sal –propuso Ven.

–Ahora las potencias Ven –dijo el gafotas –No hay raíces…

–Es el turno de los productos –dijo el pequeño –porque no hay divisiones… ¡Y ya podemos sumar y restar!

–¿Está bien, Mati? –preguntó Sal.

–Perfecto –dijo ésta.

–¡Toma, toma, toma! ¡Cómo mola! –Ven estaba entusiasmado –¡Otra!

Mati les propuso la siguiente:

–¡Qué lío Mati! –se quejó Ven –¿Por dónde empezamos?

–Por los paréntesis más interiores –dijo la gafotas –y dentro de cada paréntesis, aplicamos la jerarquía.

–Así que en el paréntesis de la izquierda primero la potencia, luego la división y después la suma… –decía Sal en voz baja.

–Y en el otro… -decía Ven –Primero el producto y luego la suma.

–Eso es –dijo Mati –Y ya tenéis resuelto esos paréntesis.

–Eso ya es muy fácil, Mati –dijo Sal muy emocionado –El paréntesis de la izquierda da 10 menos 5, 5; y el paréntesis de la derecha 10 menos 11, que es -1, si lo hacemos con los saltitos como tú nos enseñaste… Nos queda 5 por -1, que es -5, poruqe si los signos son distintos sale negativo…

–¡Toma, Sal! –dijo Ven entusiasmado –¡Somos unos cracks!

–Sí, lo sois –dijo Mati con una sonrisa –A ver ésta…

–¡Halaaaaaaaaaaaaaaaaaaaaaa!¡Mati! –dijo Ven con los ojos como platos.

–Se me ocurre una cosa –propuso la pelirroja –Ésta operación se la dejaremos a nuestros amigos lectores para que nos digan cuánto sale y nosotros nos vamos de vacaciones hasta el 5 de Septiembre, ¿qué os parece?

–¡Bien, bien! –dijo Sal –¡Vacaciones!

–Bueno, yo me quedaré hasta el lunes 30 –dijo Mati –para despedirme de todos los que no hayan podido venir hoy 😉

Tags: aritmética, jerarquía de operaciones, operaciones combinadas | Almacenado en: La hora de las tareas
23 comentarios

¡Con sólo 5 tablas!

18 de julio de 2012

(Basado en un hecho real)

–¿Cuánto es 6 por 7, Ven? –preguntó Sal.

–Espera, voy a buscar las conchitas –respondió el pequeño.

Ven dibujó 7 círculos en la arena y puso 6 conchas en cada uno de ellos bajo la atenta mirada de Gauss o, al menos, eso parecía, porque con las gafas tan modernas que llevaba la mascota uno no podía estar muy seguro de hacia dónde estaba mirando. Mati seguía ensimismada en la lectura de un libro sobre una sociedad literaria y un pastel de piel de patata.

–38, 39, 40… –Ven contaba despacio para no equivocarse.

–Pero bueno, Sal –la pelirroja volvió de su viaje por Guernsey –¿aún no te sabes las tablas de multiplicar? ¿Se te han olvidado con el calor?

–Pero, Mati –respondió el gafotas –yo tengo un método con el que no hace falta saber la tabla del 6 para nada…

–Ya, ya lo he oído –respondió ésta –Basta con pedirle a Ven que lo calcule con conchitas, ¿no?

Sal se rio a carcajadas haciendo temblar sus gafotas sobre la nariz, Ven se enfadó porque había perdido la cuenta…

–No, no es ése Mati –acabó diciendo Sal muerto de la risa –Es otro, de verdad.

–¿Sí? –preguntó Mati mirando con fingida desconfianza a su amiguito.

–Sí, de verdad –respondió éste –Con mi método sólo hace falta saber las tablas del 1 al 5.

–¿Sólo 5 tablas? –preguntó Ven que había olvidado las conchitas por un momento.

–Sí –corroboró su hermano –Si te sabes las tablas del 1 al 5, sabes las tablas del 1 al 10.

–¿¿Cómo?? –preguntó el pequeño mirando a su hermano con absoluta devoción.

–A ver, Ven. dime una multiplicación de números más grandes que 5.

–¡8 por 4! –dijo inmediatamente Ven.

–Ven, eso es 4 por 8, y está en la tabla del 4 –dijo Sal.

–Efectivamente –confirmó Mati –8 por 4 es lo mismo que 4 por 8, gracias a la propiedad conmutativa del producto.

–Y porque el orden de los factores no altera el producto, ¿no, Mati? –preguntó el gafotas.

–Esa es otra forma de expresar la propiedad conmutativa, sí –dijo ella.

–¡8 por 7! –dijo el pequeño de nuevo.

–Muy bien –dijo Sal –Ahora elegimos al mayor de los 2, el 8, y lo escribimos como (10 -2).

–Ahora tienes que multiplicar 7 por 10 –continuó el gafotas –pero eso es muy fácil, sólo tienes que ponerle un 0 detrás al 7; después 7 por 2, que también te lo sabes, porque te sabes la tabla del 2 y restarlos.

–¿Puedo hacer yo la resta con llevadas como nos enseñó Mati? –preguntó Ven excitado.

–Claro, Ven –respondió el gafotas.

El pequeño se puso manos a la obra…

–¡56! –dijo Ven con una sonrisa de oreja a oreja –¡Toma, toma, toma! ¡Cómo mola! ¡Sal eres el más mejor!

–¡Muy bien! –dijo Mati sorprendida –Es una buena aplicación de la propiedad distributiva del producto respecto a la suma.

–¿Cómo, Mati? –preguntó Sal sorprendido.

Mati escribió en su libreta y les explicó:

–Si tienes que multiplicar una suma por un número, puedes sumar primero y multiplicar después, o multiplicar el número por cada uno de los sumandos y después sumar los resultado.

–Ah, ahora lo entiendo, Mati –dijo el gafotas –Eso si lo sabía, lo que no sabía era el nombre.

–¿Y ahora qué hacemos con las conchitas? –preguntó Ven –¿Jugamos a las triangulaciones?

–

Tags: Producto, Propiedad conmutativa, Propiedad distributiva, Tablas de multiplicar, Triangulaciones | Almacenado en: La hora de las tareas
14 comentarios

¿Cuánto os estáis llevando… restando?

11 de julio de 2012

–Y te llevas 1, Ven.

–No, no me llevo ninguna, le presto 10 al 1 ¿ves, Sal? –dio el pequeño –El 9 se queda en 8 y ya se puede hacer.

–Que no, Ven –insistió Sal –Que la decena que le prestas al 1, te la llevas y se la regalas al 7…

–Pero, a ver… ¿cuántos os estáis llevando? –era Mati quien acababa de entrar –¿Otra vez jugando a los banqueros?

–¡Hola Mati! –saludaron los dos hermanos.

–Hola chicos, ¿en qué estáis?

–Estamos haciendo una resta con llevada –dijo el gafotas –y no nos ponemos de acuerdo… Ven las hace de una forma muy rara…

–Rara, no –protestó el pequeño –Me la ha enseñado mi seño y he sacado muy buena nota en Mates.

–Bueno –intervino la pelirroja –Puede haber varias formas diferentes de hacer una resta con llevadas, distintos algoritmos…

–¿Distintos qué? –preguntó Ven con la cara arrugada como una pasa.

–Distintos algoritmos –repitió ella.

–¿Qué es un algoritmo, Mati? –preguntó Sal mientras se ajustaba las gafotas.

–Un algoritmo es como una receta de cocina –empezó diciendo Mati —Una lista de instrucciones que si se siguen ordenadamente, nos permiten realizar algo, por ejemplo, una resta con llevada.

–Me encanta cocinar –dijo Ven — y restar –concluyó con una enorme sonrisa.

–¿Me explicas tu algoritmo para la resta con llevada, Ven? –le pidió Mati –¿Qué resta estabais haciendo?

–91 menos 78 –dio Ven –Como encima del 8 hay un número más pequeño, el 1, éste le pide prestada una decena al número que está a la izquierda de él, que es el 9, que se convierte en 8, y ya se puede hacer la resta.

–Ese algoritmo es perfecto, Ven –dijo Mati –¿Cuál es el problema, Sal?

–Pues que yo no lo hago así –dijo éste –Yo le daría la decena al 1 y una unidad al 7, que es el que está a la izquierda del 8…

–También es correcto tu algoritmo, Sal –dijo la pelirroja.

–¿Cuál es mejor, Mati? –preguntó el pequeño.

–El que a cada uno le resulte más fácil –respondió ella sonriendo –¿Os cuento otro?

–¿¿Otro?? –preguntó Ven con los ojos como platos –¡Vale!

–Vamos a hacer un pequeño truco –propuso la gafotas con voz misteriosa –¿Cuál es el número mayor de la resta, el minuendo?

–91 –dijo Sal casi en un susurro.

–Bien, como tiene dos cifras –continuó ella –Para nuestro siguiente truco usaremos un número auxiliar, el 100, un 1 y 2 ceros (por las 2 cifras de 91), o como decimos los matemáticos, 10 elevado a 2, que es 100.

–¿Para que quieres el 100 Mati? –preguntó misterioso y en voz baja Ven.

–Para hacer esto, ya verás…

–Pues, vaya, rollo Mati –protestó Ven –ahora tenemos una cuenta más difícil…

–Espera, cielo –dijo ésta –Vamos a hacerlas por trocitos y despacio. Primero Vamos a calcular 100 menos el sustraendo. 78. Pero eso es muy fácil: empezamos por el número de la derecha, el 8, y miramos cuánto le falta hasta 10, y al resto de los números a la izquierda, en este caso sólo está el 7, cuánto le falta hasta 9.

–Ahora –dijo Mati –sólo nos queda sumar 91 más 22 y restarle 100, pero restarle 100 es sólo borrar el uno que aparecerá en la posición de las centenas… y ¡tachán!

–¡Toma, toma, toma! ¡Cómo mola! –Ven saltaba de emoción.

–¡Me encanta tu algoritmo para la resta con llevada Mati! –gritó Sal –¿Puedo hacer yo una resta con él?

–Claro, cielo –respondió ésta.

–4321 menos 1456 –propuso el pequeño.

–¡Ahí estamos! –dijo Sal.

—Paso 1: Buscar el número auxiliar que vamos a usar –dijo Mati.

–10000 –respondió el gafotas –porque el minuendo, 4321, tiene 4 cifras, necesitamos un 1 y 4 ceros.

–Eso es… –añadió Mati.

—Paso 2: Completar el sustraendo hasta el número auxiliar, o sea, 10000 –continuó el gafotas –Esto lo hacemos completando la cifra de las unidades, 6, hasta 10 y las otras hasta 9…

—Paso 3: sumar el resultado al minuendo que era… 4321 –Sal seguía bajo la mirada atenta y de admiración de su hermano.

–¡Paso 4: Borrar el primer 1! –gritó Ven –¡Qué chulada!

–¡Muy bien, chicos! –Mati sonreía orgullosa.

–¡Me encantan los algoritmos! ¡Me encantan los algoritmos! –Ven saltaba abrazado a Gauss.

–Ya veis –concluyó ésta –Hay varias formas de hacer una misma cosa, lo importante es hacerla y hacerla ordenadamente y bien.

–Hablando de ordenar, Ven –dijo Sal –tenemos que ordenar los juguetes de nuestro cuarto.

–Vamos, chicos, –dijo la pelirroja —os echo una mano y os invito a un helado después.

Tags: Algoritmo, Artimética, Restas con llevadas | Almacenado en: La hora de las tareas
2 comentarios

¡El tuyo es más grande!

04 de julio de 2012

–Es la hora de la merienda chicos…

–¡Empanada! –dijo el pequeño Ven entusiasmado –¡Gracias, Mati!

–¡Me encanta la empanada! –Sal se relamía de gusto.

Mati ofreció un trozo a cada uno de los niños ante la atenta mirada de Gauss. Los niños miraban con recelo la porción de su hermano.

–Creo que el trozo de Ven es más grande, ¿no? –dijo finalmente Sal sin levantar mucho la voz.

–Eso no se dice, Sal –respondió el pequeño –Mamá dice que no es educado mirar los trozos de los demás… –y añadió –Pero que sepas que el tuyo es más grande que el mío.

–Bueno, Ven, si quieres podemos medir el ángulo de cada trozo con mi regla de ángulos…

–No vale, porque no son iguales de gordos los dos trozos, Sal…

–Parece que tenemos que resolver un problema de comparación de fracciones, ¿no, chicos? –intervino Mati.
–¿De fracciones? –preguntó Ven -No, de porciones de empanada.
–Eso es –confirmó Mati –Pero a lfin y al cabo, las porciones de empanadas son fracciones de empanada ¿Sabéis cómo podemos saber si dos fracciones son iguales?

–Claro, Mati –dio Sal rápidamente –Si tienen el mismo número arriba y abajo.

–No, no siempre cielo –contestó ella –Hay fracciones que pueden tener distintos los números de arriba, numeradores y los de abajo, denominadores y ser la misma fracción. Por ejemplo, mirad este ejemplo.

–¡Toma! Es verdad… –se sorprendió Ven.

–Ah, claro –dijo el gafotas –Para saber si dos fracciones son iguales sólo tenemos que hacer la división y comprobar los resultados, ¿no, Mati?

–Ése sería un método –dijo ella –Pero no siempre obtenemos el resto igual a cero tan rápido. Es decir, que hay fracciones que representan a números con muchos decimales, incluso con infinitos números decimales, y para poder compararlas y afirmar si son o no iguales, tendríamos que conocerlos todos…

–No entiendo nada… -reconoció el pequeño.

–Vamos a verlo con un ejemplo –propuso la pelirroja, vamos a comparar 65/29 y 222/99, por ejemplo. Vamos a dividir a ver qué pasa…

–¿Qué os parece¿ ¿Son iguales o no?

–Por ahora sí…

–Exacto, Ven –confirmó la gafotas –Tenemos que seguir dividiendo…

–¡Vaya! –dijo Sal –Pues no, no lo son…

–Pero Mati, si tienen infinitos números decimales, ¡no las podemos comparar nunca! –dramatizó Ven.

–Sí, sí las podemos comparar –respondió ésta –Porque no hace falta hacer la división. Para comparar dos fracciones y saber si representan al mismo número, basta con multiplicar en cruz. Os pondré otro ejemplo 7/5 y 21/15.

–¡Toma, toma, toma! ¡Cómo mola! –gritó el pequeño.

–Vaya –se sorprendió Sal –No sabía que dos fracciones podían ser tan diferentes y valer lo mismo.

–Pues sí –siguió Mati –De hecho, pueden haber infinitas fracciones que representen al mismo número, que valgan lo mismo

–Pues, vaya rollo –bromeó Ven –No te puedes fiar de las apariencias…

–Eso nunca, Ven –dijo ella con voz misteriosa –Somos científicos, ¿recuerdas? Tenemos que asegurarnos bien antes de afirmar nada –Mati le guiñó un ojo.

–Ya –continuó Sal –Sería más fácil si sólo hubiera una fracción para cada valor…

–Pues sí –corroboró Mati –Sería más fácil si sólo tuviésemos que comparar fracciones irreducibles.

–¿Irreduccibles? –preguntaron los dos hermanos a la vez.

–Sí –dijo la gafotas — Fracciones en las que el numerador y el denominador son primos, y eso ya sabéis comprobar cuándo ocurre. Pues bien, dos fracciones irreducibles son iguales sólo si el numerador y el denominador son iguales, como decía Sal al principio.

–¡Toma! –dijo el pequeño –Las irreducibles molan más.

–Pero Mati –preguntó Sal con la mirada perdida en sus pensamientos –¿De verdad que una fracción puede tener infinitos decimales?

–Huy, sí –dijo ésta –Pero de una forma especial… Os lo contaré el próximo día, ¿cómo está la empanada?

Tags: decimales, división, fracciones, máximo común divisor, números primos | Almacenado en: La hora de las tareas
1 comentario »

¿Son o no son primos?

27 de junio de 2012

–¡Mira, Gauss! –exclamó Ven –¡Son Sheldon y Penny!

–¡Qué bien, Gauss! –añadió Sal –Hoy puedes jugar con tus amiguitos.

–Querrás decir con sus primos, ¿no, Sal?

–No, Ven. Sheldon y Penny no son primos de Gauss.

–¿Cómo que no son primos? Son las mascotas de nuestros tíos –protestó el pequeño –Entonces es como si fueran los primos de Gauss, ¿no lo entiendes?

–Que no, Ven –insistió el gafotas –Que los padres de Sheldon y Penny no son hermanos de los padres de Gauss…

–¿Y eso qué importa, Sal? ¡Son primos y punto! El tío es hermano de mamá así que…

–Lo que tú quieras, Ven. Pero eso no significa que sean primos entre ellos –siguió argumentando el mayor de los hermanos –Si no son de la misma raza siquiera…

–Vaya tontería lo de la raza –bufó Ven –¡Si vamos a tener una prima negra!

–Pero ella si es nuestra prima, porque es la hija de nuestra tía…

Gauss, Sheldon y Penny observaban a los niños con caras serias, no parecían entender aquella discusión sobre conceptos de familia…

–Pero bueno… –Mati acababa de despertarse de su siesta –¡Qué serios están estos chicos! ¿Algún desacuerdo sobre algún asunto matemático? –les dijo guiñando un ojo.

–No, Mati, un desacuerdo sobre primos o no primos –dijo el pequeño Ven mirando de reojo a Sal –No tiene nada que ver con Matemáticas.

–¿Cómo que no? –bromeó la pelirroja –Los números primos son uno de los objetos que más han fascinado a los matemáticos.

–Ya, Mati –intervino el gafotas –Pero no hablamos de números primos, sino de perros primos ¿Qué son números primos, Mati?

–Un número primo es aquel que sólo es divisible por sí mismo y por 1 –dijo la pelirroja –Por ejemplo el 2, el 3, el 5…

–¡Toma! –interrumpió Ven entusiasmado –¡Los números de la sucesión de Fibonacci!

–No, no son los números de la sucesión de Fibonacci –dijo Mati sonriendo –Porque ¿cuál viene detrás del 5 en esa sucesión, Ven?

–¿Después del 5? –Ven se quedó pensando –5 más el anterior que es el 3… ¡el 8!

–Efectivamente, Ven –continuó la pelirroja –Y 8 no es un número primo.

–Es verdad –dijo Sal –8 se puede dividir por 2 y por 4.

–Eso es, Sal. El 8 tiene a 2 y a 4 como divisores distintos de 1 y de él mismo, 8 –dijo ella –¿Qué os pasa con los perros primos?

–Que Sal dice que Gauss no es primo de Sheldon y Penny y yo digo que sí.

–Ah, entiendo –dijo Mati –Lo que queréis saber es si ellos son primos entre sí.

–Eso –corroboró el mayor.

–Con los números es mucho más fácil –continuó Mati –¿Queréis que os enseñe cómo saber si dos números son primos entre sí?

–¿Primos entre sí? –preguntó Sal ajustándose las gafotas –¿Qué significa que dos números son primos entre sí, Mati?

–Que no tienen ningún divisor en común, salvo el 1, claro –dijo ésta –Por ejemplo, 10 y 9 son primos entre sí.

–No, no lo son, Mati –dijo rápidamente Ven –9 se puede dividir por 3 y 10 se puede dividir por 2 y por 5.

–Sí, Ven –siguió la gafotas –Eso significa que 9 no es un número primo, porque tiene de divisor al 3; y que 10 no es un número primo porque tiene como divisores al 2 y al 5 –Mati continuó –Pero 9 y 10 son primos entre sí porque no tienen ningún divisor en común, sólo el 1 otra vez, claro.

–Ahora lo entiendo… –dijo Ven rascándose la barbilla.

–Para saber si 2 números son primos entre sí –dijo Sal –Sólo tendremos entonces que comparar entre sí sus divisores, ¿no, Mati?

–Efectivamente –respondió ésta –Pero el problema puede complicarse cuando los números que quieres comparar son muy grandes, Sal.

–¿Cómo se hace con números grandes? –quiso saber el gafotas.

–Pues veréis –empezó a decir Mati –Lo que se hace es calcular el máximo común divisor de esos dos números. Si sale 1, es que son primos. En otro caso, no lo son.

–¿Y cómo se calcula el máximo ése, Mati? –preguntó el pequeño.

–Hay distintas maneras –respondió Mati –Os voy a enseñar el algoritmo de Euclides que es la más sencilla.

–¡Vale! –dijo entusiasmado Ven.

–Para ello vamos a usar sólo numero naturales, ¿vale? –dijo ella.

–¡Vale! –repitió Ven.

–Decidme dos números naturales grandotes y os lo explico con un ejemplo.

Los niños se quedaron pensando muy serios hasta que finalmente Sal propuso:

–¡9876!

–¡Y 3321! –añadió Ven.

–Muy bien, ahora para calcular el máximo común divisor de estos dos números, al que llamaremos MCD (9876, 3321), lo que hacemos es dividir el mayor, 9876, entre el menor, 3321, y nos fijamos en su resto. Si el resto es 0, MCD(9876,3321) es 3321.

–No, no es 0 el resto, Mati –dijo Sal –¿Qué hacemos?

–Si el resto es distinto de 0, ahora dividimos el divisor, 3321, entre el resto, 3234 –dijo la pelirroja

–Tampoco sale 0 en el resto, Mati…–protestó Ven.

–En esa caso, seguimos –respondió ella –Volvemos a dividir el divisor, 3234, entre el resto, 87.

–No digas nada, Mati –dijo Sal alegre –Ahora dividimos 87 entre 15, ¿no?

–Efectivamente, el divisor entre el resto –respondió la gafotas con un guiño.

–¡Ya lo veo! –dijo el pequeño –Ahora toca 15 entre 12, ¿a que sí?

–¡Sí! –dijo Mati con una gran sonrisa.

–Ahora dividimos 12 entre 3, ¿no? –preguntó Ven.

–Muy bien, Ven –contestó Mati.

–Y ahora sí que saldrá resto 0, Mati –dijo Sal.

–Efectivamente, eso significa que MCD(9876,3321) es 3, el último resto distinto de 0 que hemos obtenido.

–¡No son primos entre sí! –exclamó Sal.

–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven eufórico –¡Y qué fácil!

–Sí, es cierto, cielo –dijo Mati –Más fácil que como lo hacíamos en mi cole cuando yo era pequeña.

–¿No se había descubierto el algoritmo de Euclides? –preguntó Sal extrañado.

–Huy, sí –respondió la pelirroja –Este algoritmo tiene más de 2000 años de antigüedad…

–¿Dónde están los perros? –preguntó de pronto Ven.

–Creo que el máximo común divisor le dio calor –dio el gafotas riendo –porque se están dando un baño en la piscina ¿Para qué sirve saber si dos números son primos entre sí, Mati?

–Huy, buena pregunta –respondió la pelirroja –Vamos a nadar un poco con los perritos y os lo cuento después.

Almacenado en: La hora de las tareas
Comentarios desactivados en ¿Son o no son primos?

¿Ha caído dentro o fuera?

20 de junio de 2012

–Dibuja bien el círculo, Ven, si no el campeonato no será justo.

–Ya, Sal, estoy intentando hacerlo lo mejor que puedo…

–Usa la cuerda de la peonza, como si fuera un compás, ¿no?

–A ver… –el pequeño Ven se mordía la lengua muy concentrado mientras trataba de trazar el círculo. Gauss andaba a la vez que Ven dibujaba –Ya. Ha quedado casi perfecto –concluyó.

–¿Perfecto, Ven? –dijo Sal mirando aquello por encima de sus gafotas –No has aguantado bien la cuerda… ¡Eso no es un círculo!

–No, no lo es –dijo Mati –Pero es una bonita curva de Jordan.

–¿Una curva de quién? –preguntó el pequeño pensando orgulloso en que había creado algo importante.

–De Jordan –respondió Mati –Porque es cerrada y simple, no se corta a sí misma.

–Pero no es un círculo, Mati –protestó Sal –No sirve para jugar con las peonzas…

–Depende de a lo que quieras jugar –contestó la pelirroja con un guiño.

— ¿Y la curva de Jordan tiene alguna cosa chula como la cicloide? –preguntó Ven curioso y excitado.

–Pues claro, todas las curvas son interesantes –dijo la gafotas –Si alguna curva no fuera interesante, lo sería por eso, por no serlo. Como los números –terminó diciendo con un guiño.

–¿Qué tienen de interesante la curva de Jordan, Mati? –preguntó Sal.

–Las, las curvas de Jordan –respondió ésta –Hay infinitas. Cualquier deformación continua de un círculo es una curva de Jordan.

–¿Has llamado deformación a mi curva, Mati? –preguntó Ven con un medio puchero.

–Cielo –dijo Mati sonriendo –Una deformación no es nada malo. Es sólo una cambio de forma, puede mejorar la forma inicial.

–¿Cómo es una deformación continua, Mati? –preguntó el gafotas.

–Pues imagina que tienes un círculo elástico o de plastilina. Lo deformas sobre un folio de papel, no se puede ni cortar, ni pegar, sólo estirar y apretar, sin partirlo. sin superponer unos puntos sobre otros –dijo ella –Eso es, más o menos, lo que los matemáticos llamamos un deformación continua.

–¿Las inventó Jordan? –quiso saber Ven.

–No, se les llama así porque fue Camille Jordan el primer matemático que demostró que cualquier curva cerrada y simple dividía al plano en dos regiones, una la de dentro y otra la de fuera.

–Pero eso lo sabe cualquiera, Mati, ¿no? –comentó el gafotas.

–Sí, es bastante intuitivo –añadió Mati –Pero bastante complicado de demostrar con rigor, no creas. de hecho, el propio Jordan no lo terminó de demostrar, tenía algunos errores que no supo resolver. La primera prueba completa la dio Oswald Veblen, pero no era de eso de lo que yo quería hablar, chicos –continuó la pelirroja y guiñando un ojo copncluyó –No tenéis edad para hablar de Topología Algebraica.

–¿Nos enseñas a jugar con una curva de Jordan, Mati? –pidió el pequeño.

–Con mucho gusto –respondió Mati –Se trata de dibujar una curva de Jordan, lanzamos una moneda o la peonza, y tenemos que adivinar si ha caído dentro o fuera de la curva.

–¿¿Eso?? –dijo Sal muy sorprendido –Eso es de niños de la guarde, Mati…

–Sal tiene razón, Mati –dijo Ven –Es un juego un poco tonto, no te enfades.

–¿Ah, sí? –Mati sacó su cuaderno y comenzó a hacer un dibujo –¿Este punto rojo está dentro o fuera de la curva?

–¡Hala, Mati! –Ven se moría de la risa –¡Te has pasado!

–No, no, es una curva de Jordan, de niños de la guarde… –bromeó la pelirroja.

–Bueno, ésa es muy complicada… –protestó Sal.

–¿Y ésta? –Mati les mostró otro dibujo.

–¡Jajajajaja! –Ven se tronchaba –Y ésa es muy fácil, Mati. El punto rojo está fuera.

–Efectivamente –confirmó ella –Pero vamos a fijarnos un poco en este dibujo para aprender a resolver casos más complicados, ¿os parece?

–¡Sí! –dijo el gafotas.

–Vamos a pintar líneas desde ese punto hacia varias direcciones –Mati dibujó 5 líneas –¿Qué tienen en común estas 5 líneas?

–¿Que todas salen del mismo punto? –dijo Sal.

–¿Qué todas son rojas? –bromeó Ven con cara de pillo.

–No –Mati empezaba a ponerse misteriosa –Tiene que ver más con la curva de Jordan. Voy a poner otro punto, ahora verde. Y pintaré también unas líneas saliendo de él…

–¿Lo veis ya? –preguntó Mati retadora.

–¿El qué? –Ven se empezaba a poner nervioso –Cuéntanoslo ya, por favor, Mati.

–Vamos a contar cuántas veces cortan las líneas rojas a la curva de Jordan –propuso ella.

–0, 2, 2, 2 y 2 –dijo Sal.

–Ahora, contamos las verdes –dijo Mati.

–3, 3, 1, 1, y 1 –respondió Ven.

–¿Lo veis ahora? –volvió a preguntar la gafotas.

Los niños se quedaron pensando muy serios…

–¡Ya! –gritó de repente Sal –¡Los rojos son pares, y los verdes son impares!

–Efectivamente –confirmó ella.

–¿Y qué pasa con eso, Mati? –preguntó el pequeño.

–Que esa propiedad se cumplirá siempre en cualquier curva de Jordan –les explicó –Las líneas trazadas desde cualquier punto de la región interior de la curva, cortará a la curva un número impar de veces. Mientras que desde un punto en la región exterior de la curva, todas las líneas cortan a dicha curva un número par de veces.

–¡Toma, toma, toma! ¡Es verdad! ¡Cómo mola, Mati! –el pequeño Ven estaba alucinando.

–¿Os atrevéis con el primer dibujo que os puse?

–¡Sí! -respondieron al unísono los dos hermanos. Gauss ladró, no se sabe por qué. Él es así.

–La línea de la izquierda corta 12 veces… –dijo Sal –La de la derecha 16… Par ¡Está fuera!

–¡Cómo mola! –dijo Ven entusiasmado.

–Efectivamente –corroboró ella –Pero basta con dibujar una línea, todas las demás tendrán la misma paridad en el número de cortes con la curva.

–Es muy chulo este juego, Mati –confesó el gafotas –Siento haber dicho que era de niños pequeños…

–No te preocupes, Sal –respondió Mati –No pasa nada, cielo ¿Os atrevéis a colorear la región de dentro?

–¡Vamos!

–Vamos a jugar a eso, Sal –propuso el pequeño.

–Mejor, porque tus círculos… –bromeó el gafotas.

Tags: Curvas de Jordan, Teorema de Jordan | Almacenado en: La hora de las tareas
5 comentarios

Más o menos probable…

13 de junio de 2012

–¡Cara! ¡Saco yo!

–¡No vale! ¡Ha rebotado en Gauss! –Ven estaba un poco mosqueado.

–¿Otra vez? ¿Y eso qué más da, Ven?

–Se repite. Ah, se siente…

–¡Cara! ¡Saco yo! –gritó Sal de nuevo.

–No, no vale –respondió Ven, mientras Gauss resoplaba con cansancio.

–Y ahora, ¿qué pasa? –protestó el gafotas.

–No me fío de esa moneda, la has cogido de tu hucha…

–Vamos, Ven –bufó Sal –No tengo ninguna moneda falsa en mi hucha…

–¿Cómo lo sabes? –inquirió el pequeño –¿Los has comprobado como nos enseñó Mati?

–No, no lo he comprobado, Ven –respondió Sal aburrido –Pero son todas verdaderas, como las tuyas…

–¿Qué les pasa a estos chicos? –Mati acababa de llegar.

–Hola, Mati –la saludó Sal.

–Hola, Sal me quiere hacer trampa con la moneda –dijo el pequeño.

–Pesado… –bufó Sal.

–¿Por qué crees que Sal te quiere hacer trampas, Ven?

–Porque ha traído una moneda que siempre sale cara… –contestó éste.

–Eso no es verdad, Ven –se defendió Sal –Ha sido casualidad.

–Vamos a ver –intentó mediar Mati –¿Queréis que os cuente algo sobre lanzamientos de monedas y probabilidad?

–¡Sí! –contestaron los dos a la vez. Gauss resopló aliviado. Mati sacó su libreta.

–Vamos a aprender primero cómo se calcula la probabilidad de que salga cara en la moneda usando la regla de Laplace –comenzó a contarles la pelirroja.

–En el caso del lanzamiento de una moneda y calcular la probabilidad de obtener cara –siguió –el número de casos favorables es 1, que salga cara, y el número de casos posibles es 2, cara y cruz.

–Y sale 1/2 –dijo Ven –La mitad, eso ya lo sabíamos, Mati, el 50% de posibilidades…

–Sí, lo sé –afirmó ella –Con las monedas es muy fácil, pero sirve para todo. Por ejemplo, si lanzamos un dado, ¿cuál es la probabilidad de obtener una potencia de 2?

–Yo lo hago en la libreta, Mati –se apresuró a decir Sal

–Sí, pero ¿por qué no calculas la probabilidad de que Sal saque cuatro caras seguidas? –pidió Ven a la pelirroja.

–Vale, vamos a hacer un diagrama con todas los posibles resultados del lanzamiento de una moneda 4 veces –les dijo.

–Si empezamos en el punto azul y caminamos sobre las aristas azules, tenemos todos los resultados, ¿no?

–A ver… –dijo Ven señalando con su dedo sobre el diagrama —Cara, cruz, cruz, cruz… Y por aquí, cruz, cara, cara, cara...

–Si, Ven –interrumpió su hermano –Están todas.

–Ahora bien, en cada tirada, la probabilidad de obtener cara o cruz es siempre 1/2, ¿no? –continuó ella –Lo escribimos sobre las ramas.

–Bueno, chicos, ¿cuántos casos posibles hay? –preguntó Mati –Sólo tenéis que contar la columna de la derecha, cada una corresponde a un resultado posible.

–¡16! –dijo Ven con entusiasmo.

–¿Y caso favorables para obtener 4 caras? –siguió preguntando la pelirroja.

Los niños estuvieron mirando el cuaderno…

–Sólo uno, Mati –señaló Sal — Sólo cuando sale cara, cara, cara, cara.

–Entonces la probabilidad de obtener 4 caras es… –Mati dejaba la pregunta en el aire.

–¡1/16! –dijeron los 2 hermanos a la vez.

–Efectivamente, chicos –corroboró Mati –Y si os fijáis, 1/16 es el resultado de multiplicar las probabilidades que nos vamos encontrando por el camino hasta llegar al cuarto lanzamiento…

–Es verdad –dijo Sal con alegría.

–Pero Mati –intervino Ven –Cuando sean 20 tiradas, nos va a salir un diagrama, ¡enorme!

–Tienes razón, pero no hace falta hacer el diagrama –aceptó Mati –Se trata de calcular la probabilidad de una intersección de sucesos independientes, porque el resultado de cada lanzamiento es independiente del anterior. Un suceso es que la primera salga cara, otro que la segunda salga cara, el tercero que salga cara en la tercera y el cuarto, que la cuarta tirada dé cara. Cada uno de estos sucesos, tiene probabilidad 1/2, como hemos dicho, ¿verdad? Eso significa que en cada tirada de las 4, la probabilidad de que salga cara es 1/2 o sea, de un 50%.

–Ahora bien, la probabilidad de que las cuatro veces nos salga cara es la probabilidad de la intersección, y eso se calcula sabiendo que, como son independientes, la probabilidad de la intersección es igual al producto de las probabilidades.

–¿Ves, Mati? –dijo Ven con vehemencia –Es casi imposible que pase, y ha pasado

–Tú lo has dicho, Ven –dijo ella –casi imposible, pero no imposible.

–¡Que mi moneda es buena, de verdad! –se quejó Sal.

–A ver, Ven –dijo la pelirroja –Si hacemos otra vez el sorteo, ¿tú que pedirías, cara o cruz?

El pequeño se quedó un rato pensando, al cabo del cual contestó:

—Cruz.

–¿¿Cruz?? –preguntó Sal sorprendido –¿No decías que en mi moneda sólo sale cara?

–Ya… -dijo Ven mirando al suelo –Pero en realidad, creo que tu moneda es auténtica y como ya han salido 4 caras… toca cruz.

–Huy, creo que Ven ha caído en la falacia del jugador… –dijo Mati con voz misteriosa.

–¿La qué? –preguntó Sal con los ojos de par en par.

–Una falacia es una mentira o engaño –empezó a explicarles –La falacia del jugador, o falacia de Montecarlo, es la falsa creencia de que lo sucedido anteriormente en un experimento aleatorio, al azar, afectará al resultado de los experimentos siguientes.

–No entiendo nada de nada… –confesó Ven.

–Es lo que tú acabas de hacer, Ven –continuó ella –Crees que el hecho de que hayan salido ya 4 veces caras, afectará al 5º lanzamiento y no es verdad. La probabilidad de obtener cruz en el 5º lanzamiento es, de nuevo, 1/2, como siempre.

–Claro… Qué tontería…

–Bueno, Ven, esa tontería como tú la llamas, engaña a mucha gente que piensa que si sale varias 4 veces seguida cara, lo lógico es apostar a cruz por que ya toca. Y no, están confundiendo la probabilidad de obtener 5 caras seguidas con la probabilidad de obtener cara en el 5º lanzamiento.

–¡Toma, toma, toma! ¡Es verdad! –el pequeño estaba alucinando.

–Cuando lo lógico sería lo contrario –siguió la pelirroja.

–¿Lo contrario? ¿Por qué, Mati? Si cara y cruz tienen la misma probabilidad –el gafotas estaba muy intrigado.

–Ya, pero si sale muchas veces seguida cara –siguió ésta –lo que parece indicar es que la monedad no está bien compensada y que, por lo tanto, tiene más probabilidad de salir cara.

–Cierto… -se quedó pensando Sal –Si la moneda es buena, no importa lo que ha pasado antes.

–Eso es, Sal, en ese caso decimos que son experimentos independientes –confirmó la gafotas –El resultado de un experimento no depende del anterior.

–¿Y hay experimento dependientes? –preguntó Sal de nuevo.

–Sí, naturalmente –dijo Mati –Por ejemplo, si tenemos 5 bolas rojas y 3 bolas verdes en una bolsa, ¿cuál es la probabilidad de meter la mano y sin mirar sacar una bola roja?

Los niños se quedaron pensando.

–5/8 –dijo Sal

–Muy bien –sonrió Mati — La dejamos fuera ¿Y la probabilidad de que la segunda sea roja?

Sal y Ven montaron de nuevo su gabinete de resolución de problemas.

–Un momento, Mati –preguntó el pequeño –La primera que sacamos fue roja, ¿no?

–Me alegro de que me hagas esa pregunta –respondió Mati haciéndose la interesante –Eso significa que el resultado del segundo experimento depende del primero, ¿no? Son experimentos dependientes.

–¡Claro! –la carita de Sal brillaba con alegría –¿Cómo se calcula entonces, Mati?

–Vamos a verlo en el cuaderno –propuso Mati –Lo que queremos conocer es la probabilidad de que en la segunda extracción (ya hay una bola fuera) saquemos una bola roja. A esa probabilidad que queremos calcular la llamaremos P(2ªR). Para calcular P(2ªR) vamos a necesitar calcular otras probabilidades antes. Por ejemplo, la probabilidad de que la 2ª bola sea roja condicionada al hecho de que la primera que salió fuese roja, lo llamamos P(2ªR | 1ªR)

–De la misma manera, necesitaremos conocer la probabilidad de que la segunda bola sea roja condicionada al hecho contrario, es decir, al hecho de que la primera no fuese roja.

–Por último, necesitaremos usar la probabilidad de que la 1ª bola extraída fuese roja y la del suceso contrario, la de que la 1ª bola no fuese roja.

–Con todo esto, ya podemos calcular la probabilidad de que la segunda vez, extraigamos una bola roja, o sea, P(2ªR), usando esta fórmula

–Ya sólo –dijo Mati –necesitamos calcular esos 4 términos para conseguir lo que queremos ¿Me ayudáis?

–¡Sí! –dijeron los niños al unísono.

–Empezamos por la probabilidad de que la 2ª bola sea roja sabiendo que ya sacamos una y que fue roja –les dijo.

–A ver… –comenzó hablando Sal –casos posibles son 7 porque ya hay una bola menos…y casos favorables, serán 4 porque había 5 bolas rojas pero ya sacamos 1.

–¡Muy bien! ..les animó Mati –Ahora la otra condicionada, la probabilidad de que la segunda sea roja sabiendo que la primera que sacamos no lo era.

–Me toca –dijo Ven animado –Caso posibles son 7, claro, y casos favorables… 5, las 5 bolas rojas.

–Pero bueno…-Mati sonreía orgullosa –Lo que queda ya lo tenéis muy fácil

Los niños terminaron de calcular los términos que le faltaban

–¡Perfecto! –dijo la pelirroja –Ya lo tenemos todo

–¡Toma, toma, toma! –el pequeño Ven estaba alucinando.

–Me encanta, Mati –añadió el gafotas.

–Me alegro –dijo ella –El cálculo de probabilidades es muy entretenido y sencillo. Con esto y con un poco de observación, una familia española, los Pelayo, ganaron mucho dinero. Pero a vosotros todavía no os interesa el dinero, ¿verdad?

–No, ¡nos interesa el fútbol! –dijo Ven.

–Bueno, y las matemáticas –añadió Sal con una sonrisa.

—Volviendo al asunto del fútbol –empezó a decir Mati –si queréis, por ejemplo, elegir campo en el fútbol y no estáis seguros de que la moneda esté equilibrada, os enseñaré a hacer un sorteo justo.

—¿Cómo? —preguntó casi gritando Sal sonriendo esperando la respuesta de Mati.

—Muy fácil, haciendo el sorteo a dos tiradas –propuso ella –La moneda será lanzada dos veces, y los jugadores elegirán sólo entre dos posibilidades: (cara, cruz) y (cruz,cara). Si las dos veces la moneda saca lo mismo, es decir (cara, cara) o (cruz, cruz), repetimos los dos lanzamientos. Pero los dos sucesos (cara, cruz) y (cruz, cara) tienen la misma probabilidad de salir. Nadie puede enfadarse.

–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven –Vamos, Gauss, vamos a repetir el sorteo… ¿Dónde está Gauss?

–Creo que se quedó frito escuchando la explicación…

Tags: probabilidad, probabilidad condicionada | Almacenado en: La hora de las tareas
3 comentarios