(Fue esta publicación en Google+ la que nos animó a escribir esta entrada, tengo que decir que estupefactas ante las respuestas a la pregunta planteada. No se trata de saber matemáticas, se trata de anumerismo, y el anumerismo también es incultura.)
–Sale 4, Ven.
–Depende Sal, depende de lo cómo lo hagas –respondió el pequeño.
–Pero es que sólo una forma de hacerlo, Ven –repuso el gafotas –Antes que nada, las multiplicaciones y las divisiones…
–Pero, ¿qué divisiones Sal? –se quejó el pequeño –¡No hay ninguna división! Estás obsesionado con las divisiones…
–A ver, chicos, ¿qué os pasa? –intervino Mati.
–Mati, ¿a qué lo primero es multiplicar y dividir?
–Bueno, Sal –dijo la pelirroja –Si no hay ni potencias ni paréntesis…
–¡No hay nada de eso! –Ven estaba enfadándose e hinchando sus carrillos –Ni divisiones…
–En ese caso –intervino Mati sonriendo al pequeño Ven –lo primero que tenemos que hacer es la multiplicación ¿queréis que os preste mi cuaderno para poder llevarnos las operaciones que hacéis?
–Vale –dijo Ven deshinchando sus mofletes y dispuesto a copiar la operación en el cuaderno de Mati –3 por 0 es 0, eso lo sabe cualquiera… Ya sólo queda 7 menos 4… 3. Más 1… 4. Sale 4 Mati.
–Ésta era muy fácil, ¡otra! –gritó Ven muy alegre –¡Ahora con todas las cosas Mati!
–¡Allá vamos! –dijo Mati graciosamente mientras proponía una operación en el cuaderno.
–¡Hala, Mati, te has pasado! –dijo el pequeño.
–¿Qué hacemos primero, Mati? –preguntó Sal ansioso.
–Me alegro de que me hagas esa pregunta Sal –respondió la gafotas haciéndose la interesante –Porque esto me permitirá explicaros la jerarquía de las operaciones.
–¿La qué? –preguntó Ven sorprendido.
–La jerarquía, el orden en el que hay que realizar las operaciones –respondió ella –Vamos a escribirla para que no se nos olvide.
–¿Corchetes? ¿Hay corchetes en las operaciones? –preguntó Ven divertido –Yo creía que sólo había corchetes en la ropa de los bebés…
–No, no son ésos, Ven –dijo Mati –Aparte de los corchetes de la ropa, un corchete puede ser un utensilio de madera con unos dientes de hierro en el que los carpinteros sujetan la pieza que trabajan, o incluso, antiguamente, una especie de policía que detenían a los delincuentes.
–¿Un policía Mati? –Sal parecía sorprendido.
–Sí –confirmo ésta –Siempre me acuerdo de una jácara, un poema gracioso, de nuestro escritor Quevedo que decía
A la sombra de un corchete
vivo en aqueste lugar,
que es para los delincuentes
árbol que puede asombrar
–¿Cómo puede asombrarte un árbol Mati? –Ven parecía desconfiado.
–En esta jácara, el verbo asombrar –dijo Mati con un guiño –se refiere a hacer sombra.
–¡Mola! –dio el pequeño –Asombrar es una palabra polisémica y corchete también.
–Y llave, ¿no, Mati? –añadió el gafotas –Porque esas llaves que aparecen en tu jerarquía junto a los corchetes, no son para abrir puertas, ¿verdad?
–No –contestó ella sonriendo –Las llaves que aparecen en la jerarquía, igual que los corchetes, son signos que se usan para agrupar, como los paréntesis. Pero las llaves y los corchetes cada vez se usan menos para agrupar operaciones…
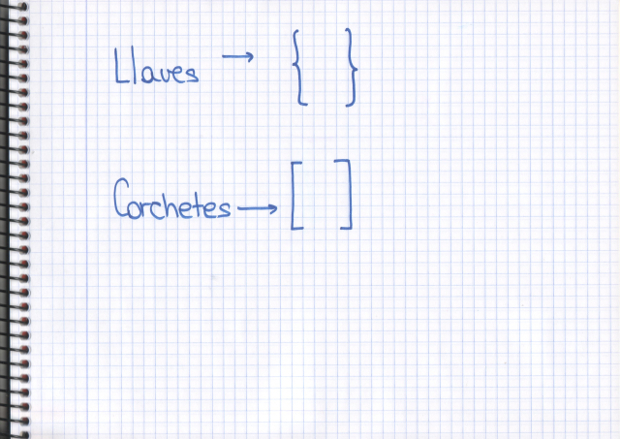
–¿Cómo son las llaves Mati? –quiso saber Ven –¿y los corchetes?
Mati los dibujó para ellos
–Vamos chicos –propuso la pelirroja –¿Os atrevéis?
–¡Sí! –respondieron al unísono y se pusieron manos a la obra.
–Primero, los paréntesis, Sal –propuso Ven.
–Ahora las potencias Ven –dijo el gafotas –No hay raíces…
–Es el turno de los productos –dijo el pequeño –porque no hay divisiones… ¡Y ya podemos sumar y restar!
–¿Está bien, Mati? –preguntó Sal.
–Perfecto –dijo ésta.
–¡Toma, toma, toma! ¡Cómo mola! –Ven estaba entusiasmado –¡Otra!
Mati les propuso la siguiente:
–¡Qué lío Mati! –se quejó Ven –¿Por dónde empezamos?
–Por los paréntesis más interiores –dijo la gafotas –y dentro de cada paréntesis, aplicamos la jerarquía.
–Así que en el paréntesis de la izquierda primero la potencia, luego la división y después la suma… –decía Sal en voz baja.
–Y en el otro… -decía Ven –Primero el producto y luego la suma.
–Eso es –dijo Mati –Y ya tenéis resuelto esos paréntesis.
–Eso ya es muy fácil, Mati –dijo Sal muy emocionado –El paréntesis de la izquierda da 10 menos 5, 5; y el paréntesis de la derecha 10 menos 11, que es -1, si lo hacemos con los saltitos como tú nos enseñaste… Nos queda 5 por -1, que es -5, poruqe si los signos son distintos sale negativo…
–¡Toma, Sal! –dijo Ven entusiasmado –¡Somos unos cracks!
–Sí, lo sois –dijo Mati con una sonrisa –A ver ésta…
–¡Halaaaaaaaaaaaaaaaaaaaaaa!¡Mati! –dijo Ven con los ojos como platos.
–Se me ocurre una cosa –propuso la pelirroja –Ésta operación se la dejaremos a nuestros amigos lectores para que nos digan cuánto sale y nosotros nos vamos de vacaciones hasta el 5 de Septiembre, ¿qué os parece?
–¡Bien, bien! –dijo Sal –¡Vacaciones!
–Bueno, yo me quedaré hasta el lunes 30 –dijo Mati –para despedirme de todos los que no hayan podido venir hoy 😉




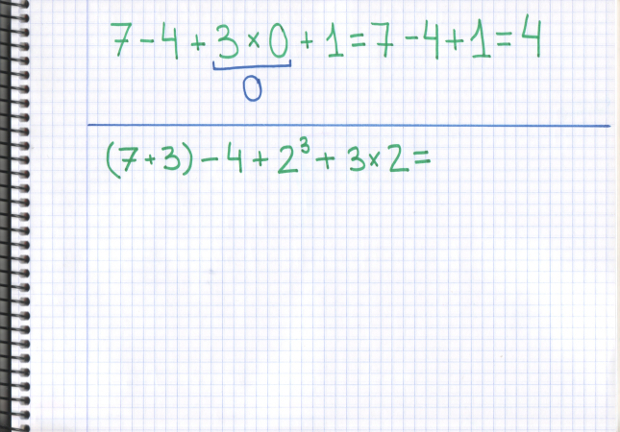

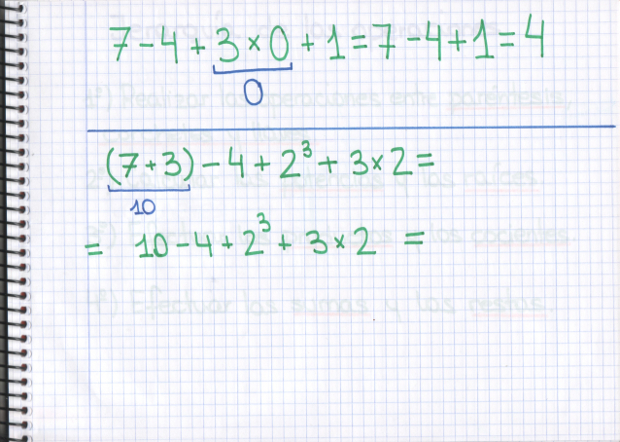

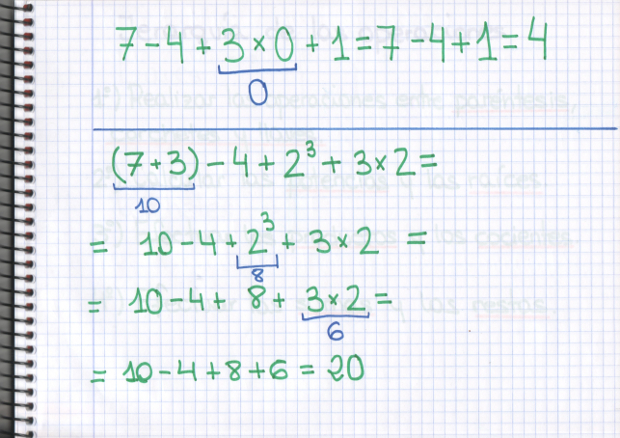
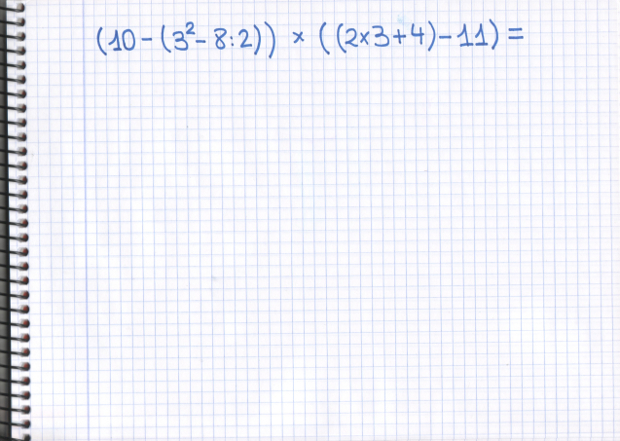





A mi me sale 6. Curioso como se han puesto de moda este tipo de «acertijos» matemáticos por internet. El último que he visto y que está causando estragos es este
48/2(9+3)
Hay dos bandos los que dicen que el resultado es 288 y los que defienden que es 2. ¿Cúal es vuestro bando?
25 julio 2012 | 10:50
Thanks for sharing such an interesting information.
25 julio 2012 | 11:19
Es una vergüenza que, al menos los adultos, no manejen este tipo de cálculos con soltura. El problema es que ya no estamos hablando de que no manejen este tipo de casos, el problema es que no saben hacerlos y todavía dicen orgullosos y creyéndose en posesión de la verdad chorradas…
Antonio, a mi también me sale 6 pero lo he hecho de cabeza todo al vuelo, igual mi memoria me ha jugado una mala pasada almacenando algún intermedio. Respecto de la «ecuación» que propones, claramente es 288, para que fuese dos debería ser 48/(2(9+3)) o 48/2*1/(9+3)
25 julio 2012 | 11:41
Buenos días,
En primer lugar, decirte que me encanta tu blog. Lo llevo siguiendo desde que entró a formar parte de 20minutos.es (antes no lo seguía por desconocimiento) y me parece que es realmente educativo.
En segundo lugar, he visto el acertijo que nos dejas y, si no me equivoco (si lo hago, mis disculpas), creo que le sobra un cierre de paréntesis justo después del primer 6. Si es así, lo ignoraré e intentaré resolverlo. Si no, espero que me resuelvas la confusión.
Muchas gracias por todo y por brindarnos con este estupendo blog. ¡Saludos!
25 julio 2012 | 11:41
o 48/2(9+3)^(-1)
25 julio 2012 | 11:42
14 – 5 – 5 + 3 + 1 = 6
Y el 48/2(9+3) es ambiguo. El paréntesis multiplica al 2 o al resultado de la división. Según lo entiendas así será el resultado.
Lo mejor es escribirlo:
48 48
___ (9 + 3) o bien _________
2 2 ( 9 + 3)
Y así preguntar el resultado.
25 julio 2012 | 11:43
Pues a mi me sale 12.
¿Jajaja, y cuando nos decís el resultado??
Y del que propone Antonio a mi me da 288
25 julio 2012 | 11:53
manufosela no hay nada de ambiguo, usa cualquier interprete matemático como mathematica, matlab o scilab por ponerte algún caso y verás que «curiosamente» todos te dan lo mismo, así como también las calculadoras científicas que daban en bachillerato (¿la casio FX era?). La sintaxis matemática indica que si un divisor contiene varios elementos estos han de ir agrupados en un paréntesis… A no ser que se exprese con boli (o lápiz) y papel de la siguiente manera:
343 * 52
—————–
3 + 7 – 2^3
que viene a ser las clásica, vamos… Esto escrito para un interprete matemático debe ser introducido como:
343 * 52 / (3 + 7 – 2^3) o bien (343 * 52) / (3 + 7 – 2^3)
25 julio 2012 | 12:02
El resultado de la operación propuesta por Mati me sale 6.
En cuanto a lo expuesto por Antonio, la respuesta correcta creo que es 288. Para que el resultado fuera 2, la operación debería ser así:
48/(2(9+3))
25 julio 2012 | 13:04
a mi el problema propuesto por mati me sale: 12
25 julio 2012 | 13:34
y la propuesta por los usuarios me da 2, al considerar que el parentesis influye al 2 y no a la division.
25 julio 2012 | 13:39
Paso por paso señores…
14 – (7 + 4 * 3 – (4 * 2 + 6)) + (4 + 6 – 5 * 3) + 3 – (5 – 8 / 2) =
14 – (7 + 12 – (8 + 6)) + (4 + 6 – 15) + 3 – (5 – 4) =
14 – (7 + 12 – 14) + (-5) + 3 – 1 =
14 – 5 – 5 + 3 – 1 =
6
25 julio 2012 | 13:49
Albert: 48/2(9+3) = 48/2 * (9 + 3) =
48
— x (9 + 3)
2
lo que es distinto a
48
————-
2 * (9 + 3)
y no porque tú consideras, creas o intuyas nada, tampoco porque yo afirme lo contrario, sino porque la sintaxis matemática es algo perfectamente definido mediante teoría de lenguajes formales, que a su vez depende de la teoría de autómatas…
http://es.wikipedia.org/wiki/Teor%C3%ADa_de_aut%C3%B3matas aquí te dejo un enlace por si quieres profundizar en la materia, cosa que no te recomiendo porque es algo bastante complejo e innecesario…
25 julio 2012 | 13:57
Estoy con Kastle, pero entiendo que este es un caso algo más ambiguo debido a la forma en la que está escrita la expresión.
Me sorprenden más las discusiones que hay sobre expresiones mucho más claras y sencillas como la que ha dado pie a esta entrada.
25 julio 2012 | 15:35
Hola. Estoy de acuerdo con Kastle, que además lo ha explicado paso por paso perfectamente.
La respuesta al de Mati es 6 (no lo puse antes porque detecté que sobraba un cierre de paréntesis después del primer 6 y esperaba que Mati lo confirmara, pues también se podría haber olvidado escribir la la apertura del paréntesis).
Respecto al que ofrece Antonio, vuelvo a estar totalmente de acuerdo con Kastle, siendo 288 el resultado.
Un saludo a todos
25 julio 2012 | 16:10
Hola, también obtengo como resultado en el problema del post 6, así que hasta ahí estoy de acuerdo con todos los que han escrito hasta ahora, jeje. En cuanto al tema de 48/2(9+3), no estoy muy versado en lo que dice Kastle de la sintaxis matemática, pero sin conocimiento de ésta lo más lógico parece ser que 48/2(9+3)=2. La explicación que doy a continuación también la ley de otro internauta. Como el 2 está justo seguido de (9 + 3), parece que ha sido sacado de factor común, es decir, que en un principio el paréntesis fuera (18 + 6), y como consecuencia de la propiedad distributiva obtuviéramos 2(9 + 3). Así pues, 48/(18 + 6) = 48/2(9 + 3) = 2. De hecho, si se introduce la función f(x) = 48/2(9+3) en el programa «Graph», se obtiene la función constante f(x) = 2. Para obtener 288 yo escribiría (48/2)(9+3).
Un saludo.
25 julio 2012 | 16:45
Perdonen, *leí. Estos días ando liado con las nuevas leyes y esto es lo que ocurre, jajaja.
25 julio 2012 | 16:46
Javi el factor común no es más que la reescritura de algo con el fin de simplificar, distintos símbolos mismo significado. La cuestión es que si es una extracción del factor común hubieran de haber sacado 6 o factor por factor 2 * 3 ya que 9 y 3 tienen como factor común el 3 también casualmente en este ejemplo igual que el 48 (3 * 2^4), quedando 48/(2*3*(3+1)) o 48/(6*(3+1)) …
Respecto a lo que hablas del programa Graph este, quizás tenga una acepción para tomar los productos sin operador como un sólo término… lo cual no debería ser así o es una extensión que se salta la norma, que siempre que los usuarios sean conscientes de ello tampoco es nada malo, pero han de ser plenamente conscientes de lo que hacen para no cometer errores semánticos ya que supongo que el programa evaluara de manera diferente 48/2(9+3) que 48/2*(9+3).
Un saludo.
25 julio 2012 | 17:20
De acuerdo, tienes razón en que, si querían sacar factor común, deberían haber sacado 6 y no únicamente 2. Ya estoy más convencido de que el resultado debería ser 288 🙂
En cuanto al Graph, en efecto, evalúa de manera diferente uno y otro. Mientras que para él 48/2(9+3)= 2; 48/2*(9+3) = 288, supongo que esto significa que, como dices, toma los productos con operador como un solo término. Es el programa que me recomendaron durante estos años de instituto, para lo que sirve está bastante bien, pero acostumbrado a él, veía claro que 48/2(9+3)= 2.
Gracias 😀
25 julio 2012 | 18:51
Buenas. El caso que proppne Antonio no es ambiguo pero lo cierto es que me he equivocado la primera vez. La prededencia es de izquierda a derecha en igualdad de prioridad de operador como es el caso de la división con el producto. Así que como explica kastle el resultado es 288. Si no hubiera visto su mensaje me hubiera apostado una cerveza a que era 2 y la habría perdido. 🙂
25 julio 2012 | 21:29
Error, error, error…
En total hay más paréntesis que se abren de los que cierran.
Error, error, error…
Eso no puede ser………………….
25 julio 2012 | 23:54
Al revés, cierran más que abren
26 julio 2012 | 1:01
Antes que nada, muchas gracias a todos por los comentarios, especialmente a Yoshi_Baraka y R2D2 que se dieron cuenta de que sobraba un paréntesis en la operación combinada propuesta (ya está corregida) y a Kastle por sus explicaciones tan claritas 🙂
Ya se ha dicho, el resultado de la operación propuesta por Antonio en el primer comentario es 288 (Kastle lo explica muy bien).
Gracias de nuevo, a todos.
26 julio 2012 | 10:35