Cada año la gripe recorre la Tierra y, aunque la llamamos igual, cada año es distinta: ataca a más población, es más dañina o más benigna. Naturalmente el virus que la produce no siempre es el mismo y detectar las distintas mutaciones lo antes posible puede ser importante para prevenir riesgos y decidir las medidas a tomar. En 2009 cuando se temió una grave epidemia de gripe producida por el virus H1N1, los científicos de Harvard Nicholas Christakis y James Fowler desarrollaron un método que permitió predecir el avance de la epidemia con dos semanas de anticipación, proporcionando un tiempo extra precioso que pudo ser bien aprovechado y que ayudo a controlar dicha epidemia que finalmente fue más benigna que otros años. La pregunta es: ¿en qué consistía la técnica de Christakis y Fowler? ¿Eran estos dos investigadores prestigiosos médicos, biólogos, farmacéuticos, …?
La respuesta es que la técnica desarrollada por los dos profesores de Harvard se basaba solo y exclusivamente en una propiedad de la Teoría de Grafos, rama de las matemáticas y es una propiedad que tiene que ver con el número de amigos en Facebook o de compañeros de relaciones sexuales que ha tenido cualquier persona y que se conoce como la paradoja de la amistad.
Dicha paradoja viene a decir que es muy probable que nuestros amigos tengan más amigos de los que tenemos nosotros y esto vale tanto para Facebook como para cualquier grupo de personas real. La versión sexual de la paradoja es que es muy probable que las personas con las que hemos tenido relaciones sexuales hayan tenido más relaciones sexuales que nosotros (pero más de uno pensará, con cierta razón, que sus amigos no están tan enganchados a internet y por eso tienen más éxito en el mundo real).
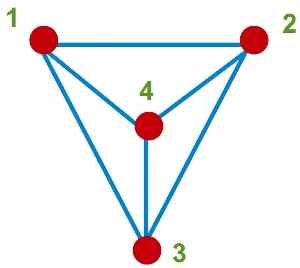
Veamos lo que queremos decir con un ejemplo sencillo, supongamos que tenemos un grupo de cuatro personas y que las amistades entre ellos las representamos con el siguiente grafo (los vértices son las personas y existe una arista entre ellos si son amigos):

En este ejemplo A, tiene un amigo, mientras que este (B), tiene tres amigos. C tiene dos amigos mientras que sus amigos tienen una media de 2,5 amigos y lo mismo ocurre con D. Así solo B tiene más amigos que sus amigos. Por tanto, en este ejemplo simple, tenemos una probabilidad de tres entre cuatro de que los amigos de alguien tengan más amigos (de media) que ese alguien.
¿Ocurrirá lo mismo en cualquier red que muestre las interconexiones (ya sean de amistad, de Facebook o sexuales) entre distintos individuos? Se puede demostrar que en cualquier grafo en el que exista una cierta variedad en los grados (número de conexiones) de los vértices esto ocurre siempre. Por ejemplo, se ha estudiado qué ocurre en Facebook en este trabajo y se llega a la conclusión de que en el 93% de los casos, los amigos de un usuario tienen más amigos que él. Más sorprendente: el número de amigos medio es de 190, pero la media de amigos de sus amigos es de 635.
¿Por qué ocurre esto?
En primer lugar, no nos deprimamos: es una propiedad que se da por la variedad de los grados y existen vértices (individuos) que tienen muchos más amigos que la media y es muy probable que estemos conectados con uno de dichos vértices, lo cual hará que se incremente la media de los amigos de nuestros amigos: la existencia de gente muy popular es lo que hace que se dé esta propiedad. Este fenómeno fue observado por primera vez por el sociólogo Scott Feld en 1991.
En realidad, esta propiedad tiene que ver con otras muchas que hace que algunas encuestas estén mal condicionadas. Por ejemplo: si a la salida de un multicine preguntamos a algunos de los espectadores que salen que cómo de llena estaba su sala, la mayoría dirá que bastante llena, porque hay más gente que sale de las salas llenas que de las semivacías. O, un ejemplo extraído de una entrada del New York Times sobre esta paradoja de la cual hemos obtenido la mayoría de la información aquí reflejada, si vamos al gimnasio, nos parecerá que la mayoría de la gente está en mejor forma que nosotros, porque la muestra la estamos extrayendo entre aquellos que están en el gimnasio y entre ellos tendremos a muchos que sean muy asiduos del gimnasio, porque a los más perezosos será más difícil encontrarlos allí.
Pero y todo esto, ¿qué tiene que ver con la gripe?
Pues lo que Christakis y Fowler hicieron fue escoger una cierta población de estudiantes que les serviría como medida y cada uno de ellos nombró a unos cuantos amigos, previsiblemente el grupo de los amigos tendrían una mayor conectividad que la población aleatoria escogida inicialmente y así fue: en el grupo de amigos se desarrolló la enfermedad dos semanas antes de media. Ello también ha llevado a proponer un método de inmunización para cuando no se desee vacunar a toda la población de una ciudad (por razones económicas, por ejemplo), se ha probado que una estrategia efectiva es escoger una cierta población inicial aleatoriamente y que los individuos de dicha población designen cada uno unos cuantos amigos: si vacunamos a estos amigos solo necesitamos vacunar a un 20%-40% de la población para evitar la difusión de la enfermedad, mientras que si no seguimos esta estrategia, necesitaríamos vacunar a un 80%-90% para alcanzar la misma efectividad.
Ya ven, a lo mejor resulta que al final los amigos de mis amigos no son mis amigos 😉





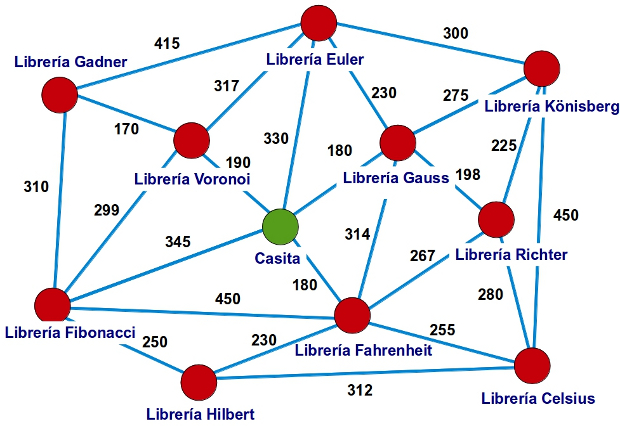

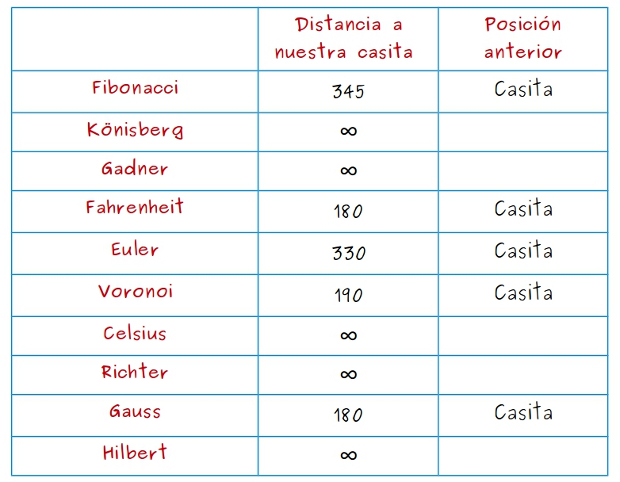



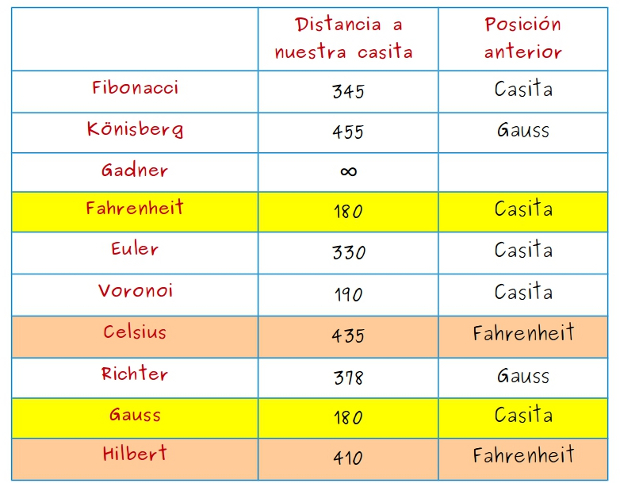






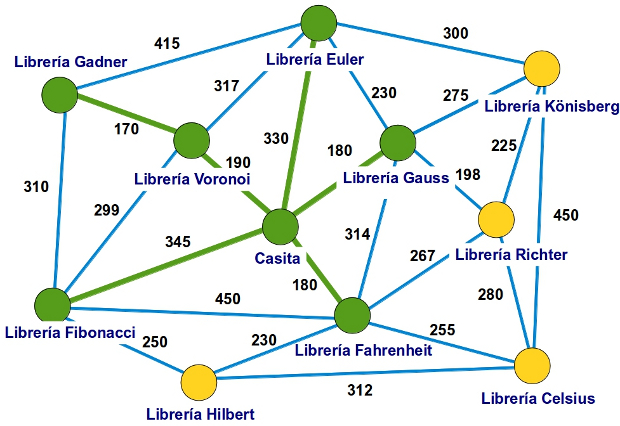
















 Efectivamente, lo es, porque se puede dibujar sin cruces entre las líneas como podemos ver en la figura siguiente:
Efectivamente, lo es, porque se puede dibujar sin cruces entre las líneas como podemos ver en la figura siguiente: