Sherlock Holmes y una bicicleta

Vamos a ponernos hoy un poco misteriosos…

En uno de los relatos cortos de Sherlock Holmes «La aventura del colegio Priory», una de las claves para resolver el misterio es decidir en qué dirección viajaba una bicicleta. Así cuando Watson plantea que puede venir en cualquiera de las dos direcciones, Sherlock le contesta:

«- No, no, querido Watson. La impresión más profunda es, naturalmente, la
de la rueda de atrás, que es donde se apoya el peso del cuerpo. Fíjese en que
en varios puntos ha pasado por encima de la huella de la rueda delantera, que
es menos profunda, borrándola. No cabe duda de que venía del colegio.
Puede que esto tenga relación con nuestra investigación y puede que no, pero
lo primero que vamos a hacer es seguir esta huella hacia atrás.»

Naturalmente Sherlock tenía razón en dos cosas: normalmente la rueda de atrás soporta más peso y la trazada de la rueda trasera puede pasar por encima de la delantera y no a la inversa. Pero lo que no está tan claro es que si tenemos las huellas dejadas por las dos ruedas de una bicicleta seamos capaces de determinar el sentido en el que viajaba ella, salvo si existen otros tipos de huellas como salpicaduras que marcan siempre como una flecha la dirección en que nos movemos.

Sin embargo, si los conocimientos de Sherlock Holmes (o de Arthur Conan Doyle) en matemáticas hubieran sido mayores, sí que se puede determinar con total precisión no sólo el sentido en el que se desplaza una bicicleta, sino algunas de las dimensiones de esta. Veamos cómo.

Simplemente hay que saber que  la recta  tangente a la curva que describe la rueda trasera siempre corta a la curva que describe la rueda delantera. Además,  la longitud del segmento de dicha tangente comprendido entre ambas curvas es siempre la misma (exactamente, la distancia entre las dos ruedas).

¿Y esto cómo lo usamos en nuestras indagaciones?

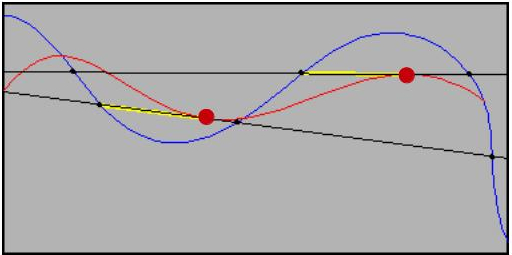
Por ejemplo, en la figura que ponemos a continuación, la curva azul no puede corresponder a la rueda trasera de la bicicleta porque en algunos puntos la tangente ni siquiera corta a la curva roja.

Sin embargo, la tangente en cada punto a la curva roja sí corta a la azul. Ya está, ya tenemos que  la curva roja corresponde a la huella dejada por la rueda trasera. Muy fácil, ¿no?

Más cosas. nos fijamos en los dos puntos rojos elegidos sobre la curva roja, en los que se ha dibujado (en negro) la recta tangente en cada uno de los dos, a la curva roja. Nos fijamos en que desde cada uno de esos puntos rojos, hay dos segmentos de la recta tangente que van desde el punto rojo en cuestión a la curva azul, uno hacia la izquierda y otro hacia la derecha. En ambos puntos rojos, los  segmentos de  tangente que van desde el propio punto hacia la izquierda (marcado en amarillo en la figura) tiene la misma longitud. Os pongo una figura con los puntos más gorditos.

Mientras que los segmentos de tangente que van desde cada punto rojo hasta la curva azul (en verde en la figura siguiente) tienen longitudes distintas.

¿Qué deducimos de esto? Pues que vamos desde la derecha hacia la izquierda y que esos segmentos amarillos nos indican la distancia entre las dos cuerdas de la bicicleta. Ea, más fácil que el mítico Sherlock 🙂

¿Otro ejemplo más?  Vamos.

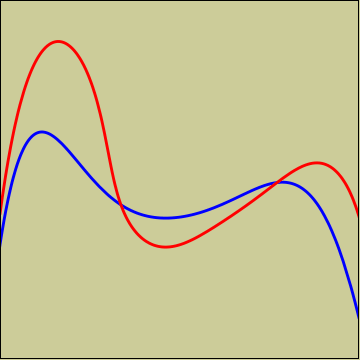
¿Cuál es la rueda trasera y en qué dirección nos movemos?  

La primera pregunta es muy fácil de responder: la tangente a la curva roja hay veces que no corta a la curva azul, por lo tanto la azul es la rueda trasera y obsérvese, como muestra la siguiente figura que las longitudes de los segmentos de dicha tangente hasta cortar la línea roja son constantes de derecha a izquierda:

Por lo tanto nos estamos moviendo de derecha a izquierda.

Para terminar,  os pongo un ejercicio: en estas trazadas, ¿cuál corresponde a la rueda trasera? ¿en qué dirección nos movemos?

Para nuestra deducción hemos usado  los siguientes elementos:

1) La rueda que marca la dirección es siempre la rueda delantera, la trasera no hace sino seguirla a ella. Esto es: en cada punto, la rueda trasera (o el plano imaginario en el que se encuentra dicha rueda), apunta hacia el punto en el que la rueda delantera toca al suelo.

2) Si intersecamos el plano que define cada rueda con el suelo obtenemos una recta para cada una de las ruedas en cada momento.

3)Y (éste es el punto clave y un poco más delicado) cada una de las rectas que hemos mencionado en 2) ha de ser tangente con la curva que define el trazado de la rueda.

A partir de 1, 2 y 3 se puede ver claramente, y ésta es la clave, que: la tangente a la curva que describe la segunda rueda corta a la curva que describe la primera rueda y la longitud del segmento de tangente entre ambas curvas es siempre el mismo (la distancia entre las dos ruedas).

PS: Podéis encontrar toda la información y generar más ejemplos en esta página de Wolfram.

Almacenado en: Ahora que los niños salieron a jugar...