Anteriormente en Mati, una profesora muy particular…
En el capítulo de hoy…
–Ya está –afirmó Ven –Una circunferencia perfecta, con centro en el punto (2,1) y radio 3. Todos los puntos de esta circunferencia están a distancia 3 del punto (2,1)
–Muy bien, Ven –dijo Mati –Te ha quedado perfecta.
–Es que he aguantado con fuerza el compás –añadió el pequeño orgulloso.
–Entonces, Mati –preguntó el gafotas –Si queremos saber si un punto está dentro o fuera de la circunferencia, por ejemplo el (4,3), lo pintamos y miramos si está dentro, encima o fuera, ¿no?
–Sí, Sal –respondió Mati –Ésa es una forma, pero no es la única. Se puede saber sin dibujar el punto.
–¿Sin dibujar? –preguntó rápidamente Ven –Tengo que dibujar el punto para medir la distancia al centro de la circunferencia y saber si está dentro o fuera.
–No, no hace falta usar la regla –insistió la pelirroja.
–Entonces, Mati –quiso saber Sal –¿Cómo podemos saber si un punto está dentro o fuera de la circunferencia, Mati?
–O sobre la circunferencia… –añadió su hermano.
–¿Recordáis cuando hablamos de las ecuaciones de la recta? –les preguntó.
–Sí –contestó Sal –La ecuación de la recta era como una una contraseña que deben cumplir los puntos para estar sobre ella, ¿no?
–Eso es –dijo Mati –Pues de la misma manera, podemos encontrar la ecuación de la circunferencia, que será como una contraseña que nos permitirá saber si un punto está sobre la circunferencia, en el interior de ésta o fuera.
–¿Nos la enseñas? –pidió el pequeño con cara de niño buenísimo.
–Con mucho gusto –respondió la gafotas guiñando un ojo –Para ello tenemos que recordar cómo se calcula la distancia entre dos puntos en el plano, como vimos cuando estudiamos las coordenadas cartesianas. Si tenemos dos puntos en el plano, (a, b) y (c, d) calculamos su distancia, que escribiremos como d((a,b), (c,d)), usando el teorema de Pitágoras.
–Para ello dibujamos un triángulo rectángulo en el que la distancia que queremos calcular es la hipotenusa, y para el que sabemos calcular la longitud de los dos catetos. La longitud del cateto vertical es la diferencia entre las segundas coordenadas de los puntos, y la del horizontal es la diferencia entre las primeras coordenadas de éstos.
–Y gracias a Pitágoras tenemos –anunció Mati muy teatrera.
–¿Y ahora, Mati? –preguntó Ven impaciente.
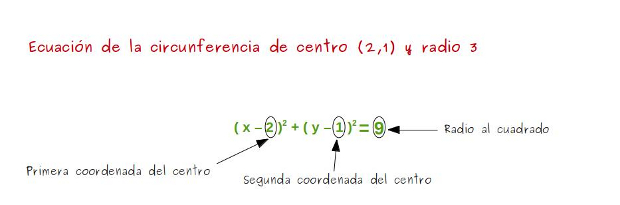
–Ahora vamos a escribir la ecuación de la circunferencia de centro (2, 1) y radio 3 –anunció la pelirroja –A ver, ayudadme, ¿qué le vamos a exigir a un punto (x,y) para que pueda estar sobre esta circunferencia?
–Que esté a distancia 3 del (2,1) –dijo el gafotas.
–Eso es –confirmó ella –Pero ya sabemos escribir la distancia entre (x, y) y (2,1) con una fórmula, la escribimos así.
–Ahora para que no salgan raíces cuadradas en la ecuación que a alguna gente les da mucho miedo –bromeó Mati –elevamos al cuadrado en los dos lados de la ecuación. En la izquierda desaparece la raíz cuadrada, y en la derecha, nos queda 9.
–Pero si con el método que nos enseñaste para calcular raíces cuadradas es muy fácil… –dijo Sal.
–¿Y para qué sirve la ecuación, Mati? -preguntó Ven.
–Pues para saber –dijo ella —si, como preguntaba Sal, el punto (4,3) está sobre ella.
–¿Cómo? –insistió el pequeño.
–Sustituyendo en la ecuación x por 4 e y por 3, y comprobando si obtenemos 9. Si no sale 9, el punto (4,3) no está sobre la circunferencia.
–No, no está, sale 8 –dijo Ven.
–Muy bien –dijo Mati –Y sin mirar el dibujo, ¿sabéis si está dentro o fuera de la circunferencia?
Los niños se quedaron pensando un rato, al cabo del cual Sal dijo:
–Creo que está dentro, Mati. Porque la distancia de (4,3) a (2,1) será la raíz cuadrada de 8, que debe ser menor que 3, que es la raíz de 9, y eso significará que (4,3) está más cerca de (2,1) que los puntos que están sobre la circunferencia, por lo tanto, está dentro.
–Muy bien, Sal –dijo Mati –Todos los puntos (x,y) que al sustituir en la ecuación den un resultado menor que 9 estarán dentro de la circunferencia, los que den mayor que 9, estarán fuera.
–¡Toma, toma, toma! ¡Cómo mola! –dijo Ven.
–¡Me encanta las ecuaciones! –dijo Sal –Las de las rectas, las de la circunferencia, y las de los sospechosos…










toypistao ¿andandará tonio la Rosa?
05 diciembre 2012 | 9:45
Como siempre jaja http://adf.ly/Fb3Sq
05 diciembre 2012 | 10:11
Pero…. pero… pero. Yo soy de letras, SOY DE LETRAS.
Desde mi nombre puedes ir a mi blog de adopción de cachorritos.
05 diciembre 2012 | 11:05
Me encanta!!!; Qué tiempos aquellos donde se aprendían estas cosas. Circunferencia = El lugar geométrico de los puntos del plano que equidistan de un punto fijo. Qué fácil era al principio y qué trivial es ahora (para un ingeniero industrial).
Saludos
05 diciembre 2012 | 17:15