–¿Eso es Marte, Ven?
–¿Qué pasa, Sal? Está casi perfecto…
–¿Perfecto? Marte es una esfera…
–No, no lo es, me lo dijo Mr. Green. Se parece más a una elipse.
–Ya, pero es casi redondo, dibuja un círculo, por Gauss…
La mascota gruñó un poco, pero con cierto orgullo, le gustaba llevar el nombre del Príncipe de las Matemáticas.
–Eso he hecho, un círculo, Sal –Ven empezaba a enfadarse.
–¿Un círculo? Eso más que un círculo ¡parece una patata!
–¿¿Una patata?? –la carita de Ven se iba encendiendo cada vez más.
–Bueno, bueno, bueno… –Mati acababa de llegar –¿Estáis preparando alguna comida con patatas?
–Hola Mati –la saludó Sal –No, estamos haciendo un mural con Marte y el Curiosity para el colegio, queremos contarles a todos lo que nos contó Mr. Green, y Ven ha hecho un círculo que parece una patata.
El pequeño Ven arrugó su carita completamente, maś enfadado que nadie en el mundo. Gauss se puso junto a él y frunció el ceño también.
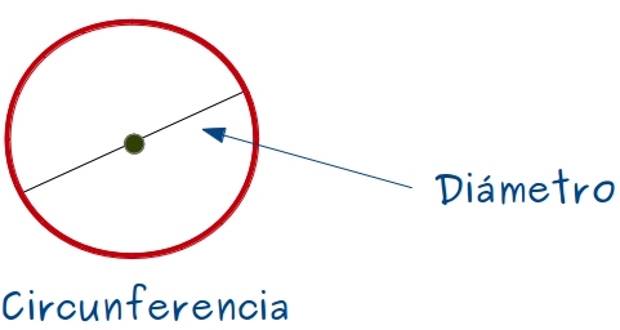
–Hombre, Sal, una patata, una patata… no es –dijo la pelirroja –Pero si queréis, os enseño a dibujar círculos, o mejor dicho, circunferencias.
–¿No es lo mismo, Mati? –preguntó Ven desfrunciendo un poco el ceño.
–No, la circunferencia es la línea curva y cerrada, con la propiedad de que todos los puntos sobre ella están a la misma distancia del centro –contestó ella –El círculo está formado por todos los puntos encerrados por la circunferencia que tienen la propiedad de que están a una distancia del centro de la circunferencia menor o igual que el radio.
–¿Qué radio, Mati? –preguntó Ven muy serio.
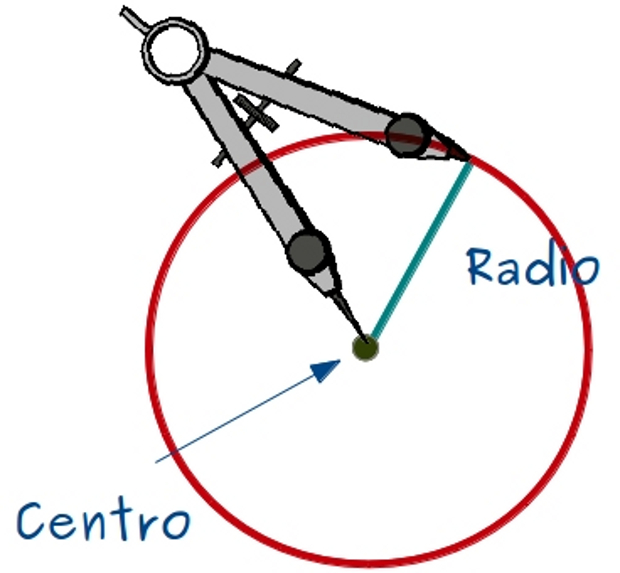
–Una circunferencia, es una curva cerrada en la que todos los puntos de la misma están a la misma distancia de un punto determinado, que llamamos centro. Pues bien, el radio de la circunferencia es esa distancia, la de cualquier punto de la circunferencia al centro.
–Ah, ya.. –acepto el pequeño.
–Además del radio –siguió Mati –hay otros elementos en la circunferencia, y en el círculo, que tienen nombre propio. Por ejemplo, el diámetro.
–¿Qué es el diámetro, Mati? –preguntó el gafotas.
–Un diámetro de una circunferencia es un segmento uniendo dos puntos de ésta que pasa por el centro.
–¿Y si el segmento no pasa por el centro, Mati? –preguntó Sal.
–En ese caso, a ese segmento se le llama cuerda –dijo ésta.
–Bueno, Mati –intervino Ven impaciente –¿Nos enseñas a dibujar círculos o circunferencias?
–Claro, Ven –respondió ella — ¿Cómo quieres que sea? ¿Qué circunferencia quieres dibujar?
–¿Cómo? Una –dijo el pequeño.
–Pero hay muchas formas de definir una circunferencia –continuó Mati –Por ejemplo, podemos definir una circunferencia diciendo cuál es su centro y su radio. Para ello, solo hay que elegir en qué punto colocamos el centro y abrimos el compás tanto como nos indica el radio.
–O bien –siguió ella –Podemos definir una circunferencia eligiendo el centro y un punto que esté sobre la circunferencia.
–Ah, ya sé –interrumpió Sal –Pinchas en el centro y abres el compás hasta el punto que quieres que esté en la circunferencia.
–Eso es, sí –afirmó ella.
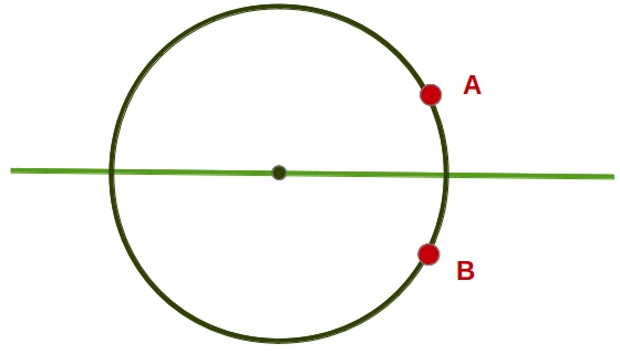
–¿Y si quieres que la circunferencia pase por 2 puntos? –preguntó Ven.
–En ese caso, depende –dijo Mati –Si esos dos puntos son los extremos de un diámetro de la circunferencia buscada, hay una única circunferencia con esa propiedad. Para ello, calculamos el punto medio del segmento que une los dos puntos, y ése será el centro. Para el radio, basta con pinchar sobre el centro y abrir hasta cualquiera de los 2 puntos iniciales.
–¡Mola! –exclamó Ven.
–¿Y si los 2 puntos no son extremos de un diámetro, Mati? –preguntó Sal.
–En ese caso –respondió ella –Hay infinitas circunferencias que pasan por esos dos puntos.
–¡¡Sí, claro!! –dijo Ven –¡Qué bruta!
–¡Jajajajajajajajajajaja! –la pelirroja no pudo reprimir una carcajada –Que sí, chico de poca fe, pero te lo voy a demostrar –y añadió guiñando un ojo –Me gusta que desconfíes de lo que no te demuestran.
–¡Venga, demuéstralo! –pidió Ven con una sonrisa de oreja a oreja.
–Dibuja dos puntos en la libreta –le pidió Mati y Ven los dibujó –Ahora dibujaremos la mediatriz entre esos 2 puntos.
–¿¿Cómo?? –preguntó Sal.
–Muy fácil –anunció la pelirroja –Para calcular la mediatriz entre los puntos A y B, primero pinchamos en A y hacemos un círculo grandote; después pinchamos con esa misma apertura en B y hacemos otro círculo; estos dos círculos, se cortan en 2 puntos. Basta con unir esos dos puntos y tendremos la mediatriz AB, y de paso, el punto medio entre A y B, que será donde a mediatriz corte al segmento AB.
–¿Y? –preguntó el gafotas.
—Cualquier punto sobre la mediatriz AB está a la misma distancia de A que de B –les dijo –Si pincho con el compás en cualquier punto de la mediatriz y abro, por ejemplo, hasta A, puedo dibujar un círculo que pasará por A y por B.
–¡Ajá! –aceptó el pequeño.
–Pues bien, Ven –siguió ella –Puedes hacerlo en cualquier punto de la mediatriz, ¡y son infinitos!
–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven entusiasmado.
–Claaaaro… –añadió Sal con los ojos abiertos de par en par.
–¿Y si tenéis 3 puntos? ¿Cuántas circunferencias pensáis que podáis encontrar pasando por los 3? –preguntó Mati a los niños.
–¡¡Infinitísimas!! –gritó Ven levantando los brazos.
–¿Infinitas? –dijo Sal mirando a su hermano por encima de sus gafas.
–No, menos –dijo Mati.
–¿Infinito menos 100? –dijo Ven con sonrisa pícara.
–Infinito menos 100 es infinito, Ven –dijo el gafotas.
–Ya lo sé –respondió éste.
–Pues no, la respuesta es … –dijo Mati e hizo una pausa dramática –Sólo una.
–Mati… –dijo Ven con cara de desconfiado –Eso tendrás que demostrarlo.
–Con mucho gusto –dijo ella mientras hacía una graciosa reverencia –Dibuja 3 puntos en el papel, A, B y C.
Los niños dibujaron los 3 puntos como les pidió Mati, ella les dijo:
–Ahora pintad las mediatrices AB, BC y AC.
Los niños las pintaron con su regla y compás.
–¿Veis que las tres se cortan en un punto? –les preguntó.
–¡Ajá! –dijo Ven.
–Pues ése es el único punto que está a la misma distancia de los 3 a la vez –les dijo –Por lo tanto, es el centro de la única circunferencia que pasa por los 3 puntos.
–¡Tomaaaaaaaaaa! –dijo Ven.
–Es verdad –aceptó Sal.
–Además –continuó Mati –Si pintéis el triángulo ABC, ese punto se llama circuncentro del triángulo ABC, por ser el centro de la circunferencia que rodea al triángulo.
–¡Qué guay! –exclamó Ven.
–Oye, Ven, por cierto –añadió Sal –¿Por qué no usas el compás para dibujar Marte?
–Ya te he dicho que no es esférico, Sal, ¡es elipsoidal! –protestó Ven.
–Ya, pero parece más una esfera que una patata…











Genial entrada. Felicidades!!
http://areaestudiantis.com/
28 noviembre 2012 | 10:32
Muy bueno http://adf.ly/EaLt1
28 noviembre 2012 | 14:37
Creo que, según lo interpreto yo, hay una errata …, al principio donde dice elipse… ¿no debería decir elipsoide, que es lo guarda cierto parecido con la esfera?.
28 noviembre 2012 | 15:03
Hola Mati. Sigo tus aventuras y me encantan. Hoy quiero comentar el uso que haces del gerundio que, al parecer, hay quien opina que es incorrecto:
«…Un diámetro de una circunferencia es un segmento uniendo dos puntos de ésta…».
Según la Fundéu:
Gerundio del nombre o gerundio especificativo
«Es un galicismo. Este gerundio incorrecto ocupa el lugar donde normalmente aparecería un adjetivo especificativo o una oración subordinada adjetiva. Es decir, cuando el gerundio se utiliza en sustitución de que + verbo en forma personal, sin comas, para calificar a un sustantivo, su uso es incorrecto, dado que su función es especificativa.»
Lo correcto según la Fundéu sería:
«…Un diámetro de una circunferencia es un segmento QUE UNE dos puntos de ésta…».
Hay una anécdota de Valle-Inclán. Don Ramón necesitaba una transfusión, se supo y se presentaron un montón de escritores. Echegaray aprovechó la ocasión para intentar quedar como un caballero ( cuando había sido un perfecto rufián al impedir que la prosa magistral e insuperable de Valle se alzara con los premios) y se presentó también. Cuando el médico, emocionado por el gesto, se lo dijo a Valle, este le espetó:
– ¡ Doctor, ni se le ocurra ¡No quiero la sangre de ese!¡ La tiene toda llena de gerundios!
De aquí:
http://historiasconhistoria.es/2009/08/27/el-genio-de-don-ramon-de-valle-inclan.php
¡Un saludo y gracias!
29 noviembre 2012 | 15:29
No es una patata, es un círculo con un renormamiento equivalente un tanto irregular 🙂
29 noviembre 2012 | 15:45