–¡Punto mío!
–¿Qué dices, Ven? ¡Ha dado en la línea! ¡Eso es dentro!
–¿¿Dentro?? De eso nada, Sal, ha dado fuera de la línea.
–Ha dado sobre la línea –dijo Sal muy seguro, tranquilo y convencido.
Gauss miraba fijamente la línea tratando de posicionarse en aquella discusión. Pero no lo tenía tampoco muy claro. Al fin y al cabo, adoraba a sus dos dueños y no le gustaba tomar partido. Mati se dejaba querer por el sol y la brisa marina pensando en teoremas y conjeturas.
–Que sí, que ha dado sobre la línea, ¿lo ves? –dijo Sal sin perder los nervios.
–No, Sal, ¡ésa es una marca antigua! –Ven estaba cada vez más rojo y nervioso. Se le empezaba a rizar el pelo, no se sabe muy bien por qué.
–Huy, qué acalorados estáis, chicos –Mati salió de su ensoñación matemática–¿Qué os pasa?
–Nada, Mati –dijo Sal –Sólo que Ven está tratando de hacer trampas…
–Nada de eso, Mati –interrumpió el pequeño muy excitado –Ha dado fuera de la línea, ¡punto mío!
–Que no, Ven, pesado, que ha dado sobre la línea –insistió el gafotas.
–¿¿Estás de broma?? ¡La bola no entró! –Ven estaba cada vez más enfadado, casi tira la raqueta al suelo, pero no lo hizo porque era un regalo de sus abuelos y no quería romperla.
–Entiendo… –añadió la pelirroja tratando de buscar una salida a aquella situación –Todo depende de decidir si el punto donde la bola tocó el suelo estaba sobre una línea o no…
Mati se quedó cómicamente pensando, los niños la miraban esperando, cada uno por su lado, que le diera la razón. Gauss miraba al mar…
–En Matemáticas es mucho más fácil saberlo, ¿sabéis? –comenzó a decir Mati –Se trata simplemente de usar una ecuación.
–¡Toma! Nosotros ya sabemos ecuaciones, Mati –dijo el pequeño con alegría –Nos enseñaste el otro día.
–Es cierto, Ven –respondió Mati –pero las ecuaciones de las que os hablo, son un poco diferentes, aunque también muy sencillas.
–¿Por qué son diferentes, Mati? –preguntó inmediatamente Sal.
–Porque, por ejemplo, en estas ecuaciones, no hay una sola letra misteriosa, o incógnita, la x –dijo Mati –sino que aparece con una de sus mejores amigas, la y, que también va de incógnita.
–Hum, interesante… –añadió Ven –Así que tenemos dos sospechosas…
–Sí y no –contestó ella.
–¿Sí y no? –Sal estaba cada vez más intrigado y entregado.
–Veréis en realidad de lo que se trata es de saber si un punto está o no sobre la línea o recta, que a los matemáticos nos gusta llamar rectas a las líneas rectas, porque hay otras líneas que son curvas –Mati hizo una pequeña pausa y continuó –Para ello lo que solemos hacer es dar una ecuación de la recta, que es, podríamos decir, como una contraseña que deben cumplir los puntos para estar sobre ella.
–¿No hay sospechosos entonces, Mati?
–No exactamente, Ven –continuó la gafotas –No se trata de desenmascarar a x y la y para conocer su valor como hicimos con las ecuaciones del otro día, sino comprobar si el punto que elijamos cumple la ecuación (la contraseña) para estar en esa recta.
Los niños seguían mirando a Mati con los ojos brillantes con las raquetas en ristre, esperando que ella continuara contándoles aquella historia de contraseñas para pertenecer al club de la recta. Gauss se echó a dormir aprovechando que no tenía que ir a buscar las bolas cuando éstas salían despedidas.
–Os lo explico con un ejemplo –propuso Mati mientras sacaba su libreta del bolso de la playa –A ver si así os resulta más fácil
–¡Sí, por favor! –dijo
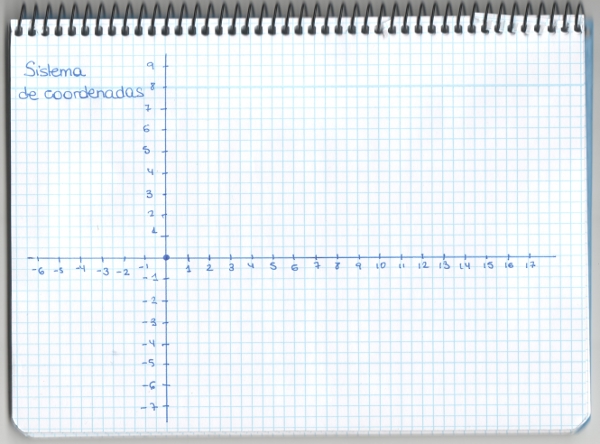
–Lo primero que necesitamos es un sistema de coordenadas, por ejemplo, cartesianas.
–¿Por qué pones números negativos, Mati? –preguntó Ven.
–Son números enteros, ¿recuerdas? –dijo ella –Para indicar que estamos a la izquierda o por debajo del origen. Los positivos nos indican que estamos a la derecha o arriba del mismo. Y con este sistema de referencia, sabemos las coordenadas de los puntos como cuando jugábamos a los barquitos.
–¡Mola! Como estamos en la playa… –Ven se iba olvidando poco a poco de la polémica bola…
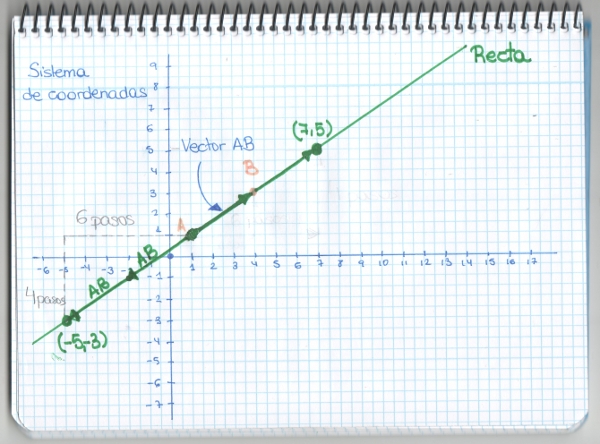
–Voy a dibujar una recta –continuó Mati.
–Para poder conseguir la ecuación de esta recta, es decir, la contraseña para que un punto esté sobre ella, necesito obtener algunos datos de la misma. Para ello vamos a usar, por ejemplo, a dos miembros de ella, dos puntos que pertenecen a este club. Necesitamos las coordenadas de 2 puntos sobre ella…
–Éste y éste –dijo Sal a la vez que señalaba 2 puntos sobre el cuaderno de Mati.
–El (1,1), le llamaremos A…y el (4,3), le llamaremos B –añadió Mati.
–Muy bien. Ahora –dijo la pelirroja –Voy a darle un nombre y un apellido, unas coordenadas, a la flechita que va desde A hasta B. A esa flecha le llamaré vector AB.
–¿Cómo se saben las coordenadas de una flecha, Mati? –preguntó Sal intrigado.
–Las coordenadas de una flecha o vector serán las siguientes: la primera coordenada nos indica cuánto nos movemos hacia la derecha, si es positiva, o hacia la izquierda, si es negativa; la segunda coordenada nos dirá cuántos pasos damos hacia arriba, si es positiva, o hacia abajo, si es negativa.
Los niños se pusieron a contar los pasos que indicaban el vector AB de su dibujo.
–Tres pasos a la derecha… –mascullaba Ven –y dos hacia arriba…¡(3,2), Mati!
–También se pueden calcular las coordenadas del vector AB restando a las coordenadas de B las coordenadas de A –les contó Mati.
–¿Cómo se restan coordenadas, Mati? –quiso saber Sal.
–Ah, claro. La primera con la primera y la segunda con la segunda –respondió ésta.
–Muy, muy bien, chicos –la pelirroja estaba orgullosa de sus amiguitos — Y claro, las coordenadas del punto B es igual a la suma de las coordenadas de A y del vector AB.
–¡Toma, toma, toma! ¡Es verdad! –el pequeño ya estaba alucinando.
–¿Qué pasa si sumamos al punto A dos veces el vector AB? –preguntó ella.
Los niños se quedaron pensando y mirando al dibujo, hasta que, finalmente, Sal dijo:
–Que andaríamos 6 pasos a la derecha y 4 hacia arriba y llegaríamos… a este punto –señaló el gafotas sobre el dibujo –Al de coordenadas (7, 5).
–¿No es el mismo resultado que si hacemos esta cuenta? –cuestionó Mati a los niños.
–¿Cómo se multiplica 2 por (3,2)? –preguntó el gafotas — ¿A la primera coordenada? ¿O a la segunda?
–A las dos –respondió la gafotas.
–¡TOMAAAAAAAAAAAAA! –gritó Ven entusiasmado –Sale (7,5)
–Claro –continuó Mati sonriendo –Todos los puntos de esa recta se pueden conseguir sumando a A el vector AB un número de veces o restándolo.
–¿Cómo que restándolo?
–A ver, ¿hacéis este cálculo? –les pidió
Los niños se pusieron manos a la obra.
–¿Cómo se hace 1-6, Mati? –preguntó el pequeño.
–Andando 6 pasos a la izquierda en la regleta, ¿no te acuerdas? Y 1-4 se calcula dando 4 pasos a la izquierda del 1 también en la regleta.
–Huy, es verdad… –se disculpó Ven –A ver qué nos sale… (-5, -3)… ¡Toma! ¡Es verdad! ¡También está sobre la recta! –el pequeño Ven disfrutaba cada descubrimiento.
–Bueno, pues ya sabemos que para que un punto esté sobre la recta, debe cumplir esa contraseña o condición: que debe ser igual que el punto A más el vector AB multiplicado por un número. O sea que la ecuación que debe cumplir un punto (x,y) para pertenecer a esta recta es la siguiente
–Y eso, ¿cómo se usa, Mati? –preguntó sal muy serio.
–Vamos a ver, decidme un punto sospechoso de pertenecer a la recta…
Los niños miraron el dibujo.
–El (7,5) –propuso Ven McEnroe.
–Muy bien –dijo Mati –tomamos x como 7 e y como 5 y susitituimos en la ecuación. (7,5) pertenecerá a la recta si k nos da el mismo valor en las dos ecuaciones.
–Efectivamente, (7,5) cumple la ecuación, para el valor de k igual a 2. Es un miembro de la recta –concluyó Mati.
–¡Toma, toma, toma! –el pequeño saltaba de alegría.
–Ahora el (10, 9) –propuso Sal animado.
–Vamos a ver si (10, 9) se sabe la contraseña…
–¡Ja! ¡Te pillamos (10,9)! Tú no eres del club de la recta… –Ven estaba disfrutando con aquello.
–Es alucinante, Mati…–Sal miraba al cuaderno y se ajustaba las gafas.
–Las Matemáticas siempre lo son –respondió ella con un guiño –Pero hay otras formas de detectar a los miembros de una recta. Os las enseñaré. Vamos a dejar sola a k en las dos ecuaciones como ya sabemos, deshaciendo en orden inverso todas las operaciones que la ocultan…
–Cuando igualamos las dos ecuaciones porque las dos valen lo mismo, k, tenemos una nueva ecuación de la recta, que se llama ecuación continua.
–Así, cada vez que tengamos dos puntos de una recta podemos calcular suu ecuación continua sin más que hacer esto
–¡Qué chulo! –exclamó Sal — ¿¡Cómo la usamos para saber si, por ejemplo, el (1,0) pertenece al club?
–Muy fácil –dijo Mati –Cambiamos x por 1 e y por 0 y vemos qué pasa.
–Ajá, no eres de nuestro club, forastero… –dijo Ven cuando descubrieron que el (1,0) no pertenecía a la recta.
–¿Os gusta, chicos? –continuó la pelirroja –Pues aún podemos escribir la ecuación de la recta de otra forma.
–¡Venga! –la animó Sal.
–Usando nuestras técnicas de desenmascaramiento vamos a tratar de llevar todo al primer miembro de la ecuación, ya veréis…
–Ya tenemos otra ecuación de la recta –dijo Mati –La ecuación implícita.
–Prueba con el (4,2), Mati –pidió Ven ansioso.
–¡¡Yo! ¡Yo lo hago! –intervino Sal –Cambio x por 4…cambio y por 2…
–¡Otro! Hemos pillado a otro que no está –Ven lo pasaba en grande.
–Pues además de decirnos si un punto pertenece o no a una recta, con esta ecuaciones podemos calcular todos los puntos sobre ella que queramos –dijo Mati.
–¿¿Cómo?? –preguntaron los dos niños a la vez.
–Elegid un valor para la x –les propuso.
–¡10! –gritó Ven.
–Estupendo –contestó la pelirroja –ponemos 10 en lugar de x y vamos a ver cuánto vale y…
–¡Toma, toma, toma! ¡CÓMO MOLA! –a Ven se le salían los ojos de las órbitas.
–¡Me encanta, Mati! –Sal estaba también entusiasmado.
–Pues aún hay más…–respondió ella con tono de misterio –pero ésas la dejaremos pendientes... Ahora vamos a dar un paseo por la playa.
–¡Vale! –dijo Ven –Pero que sepáis que la bola no entró…










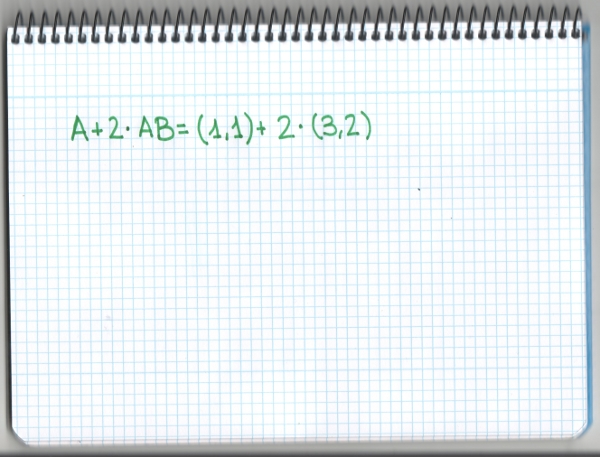

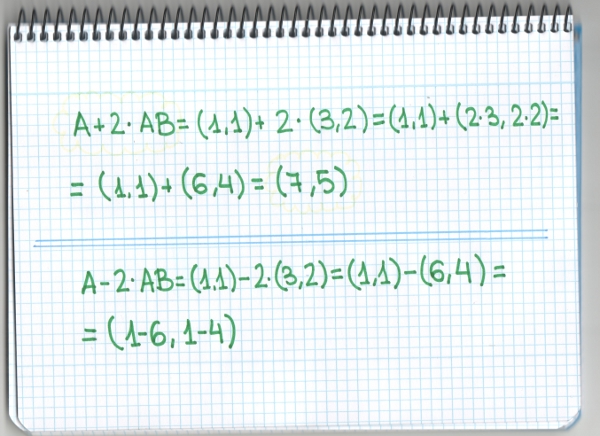










Si los franceses leyeran esto seguro que estos días en Roland Garros, el algoritmo del Ojo de Halcón se inspiraría en las ecuaciones de Mati.
23 mayo 2012 | 9:44
Estoy, por vuestra culpa, matando la ignorancia
soñando de nuevo con hadas y alegres mariposas;
me asombran vuestras mentes luminosas y me encantan
vuestras mágicas historias tan llenas de fragancia,
tan divertidas y, en fin, tan generosas
en pro de nuestra siempre linda infancia.
23 mayo 2012 | 11:37
Pues supongo, @derivando, que los franceses sí que sabrán de ecuaciones de la recta, pero igual no les interesa 😉
wow, @Manuel, gracias por tu comentario, de verdad. Me ha emocionado :’)
Clara Griima
23 mayo 2012 | 11:42
A mi modo de ver, el intento es bueno… pero ha quedado un poco asi asi… no me parece conveniente la historia de alrededor si nada tiene que ver demasiado difusamente con lo que se explica y me parece que tampoco sirve de gran cosa adornarla conversaciones que intentan hacerlo parecer guay sin serlo, porque hacen un poco pesada y larga la explicacion.
El planteamiento de partida deberia ser algo que solucione un problema que se nos pueda presentar a todos y cuanto mas util en el dia a dia mejor. Que vaya directo al asunto pero que sea con explicaciones muy muy claras, evidentes, inicialmente sin notaciones complicadas y que no necesiten por su claridad demasiado de recordar lo anterior que hayas explicado para que este claro esto nuevo y por tanto que nos motiven a seguir avanzando en comprender la explicacion. En este sentido algo en el sentido aunque no has ido mucho mas alla, si te he visto etiquetando los elementos de las formulas para que se vea facil que es cada cosa (la notacion matematica formal es buena para el que ya sabe y no quiere perder tiempo buscando lo que quiere, pero es pesima como medio para aprender sobre ella).
Es decir, lo que tiene que quedar claro es la matematica en si a nivel conceptual en tu cabeza y si es posible enfocarlo primeramente de forma visual completo dejando debajo el analitico de esa parte si quieres (de hecho puedes hacer un analitico mas simplificado para hacer mas facil el paso de visual a formal y debajo dejar el formal), por lo demas siempre es bueno dar varios enfoques sobre el mismo tema, porque los que reciben el conocimiento tienen el suyo propio ordenado de distintas maneras y la finalidad es que ese conocimiento encaje en la forma en que analiza las cosas realmente el que escucha la explicacion. Y eso es la parte quiza mas dificil de la didactica, hacer que los conocimientos que das encajen con la cotidianidad y conocimientos del que los recibe para este los interiorice, empiece interrelacionar internamente ese conocimiento de forma real y que tenga capacidad luego de usarlo para su dia a dia o de recomponer el conocimiento analizandolo si un dia lo olvidara.
23 mayo 2012 | 12:04
Jose si tan claro lo tienes hazlo tu. ¡Y pon las tildes!
23 mayo 2012 | 12:42
Yo creo que más que recta fue una parábola lo qu ehizo la bola. No, no es por llevar la contraria, sino por saber de ecuaciones de parábolas también.
Yo me sé una parábola que dice: a quien buen árbol se arrima, buena sombra le cobija. Bueno, si no es parábola, es palabrería, que más o menos es lo mismo, o no, según se mire, y si se mira de diferente punto de fuga o de vista, también pudiera nacer otra realidad que mostrara de igual manera la posibilidad de concretar en realidad manifiesta la ecuación teórica del refranero, modificando la parábola o palabrería diciendo que quien a buen árbol se arrima algún pájaro le caga encima, si bien habría que manejar otras variables, como la estación, el tiempo de tumbada o sentada bajo el árbol, las ganas del pájaro de hacer popó y su puntería o cosa azarosa, la trayectoria, fuerza de rozamiento del viento, compactación de la bola y todo eso que mismamente me hace rechazar l idea de poder llevar a cabo tal estudio por mi mismo al sentirme incapaz de realizar tanto cálculo y contener tanta variabilidad dentro de mi cerebro como el de esos matemáticos a quien desde siempre he admirado tanto por ser capace de ver en las fórmulas de números para mí casi sin sentido, la otra realidad de las cosas,que acaba siendo mayor realidad que la sensitiva, generalmente.
Muy buen post.
23 mayo 2012 | 14:24
Me tenían en el cole por genio en matemáticas. Perdí esa capacidad sin saber bien por qué. Luego me pasé a letras y me pusieron de muy buen ejemplo en el Insti. Al final no sé de lo que va la recta de la existencia, porque es recta bajo el influjo insuperable de cronos, aunque siempre queda la tonta, ilusa, pero hermosa ilusión de creernos por encima del tiempo y volver a disfrutar de aquellos lindos momentos en que los números te hablaban, y podías oírlos tan claramente… Mira, me ha salido una lagrimita y todo recordando…Ay, las matemáticas… dónde y por qué dejaron de quererme tanto…
23 mayo 2012 | 14:32
Yo creo que es un buen diálogo, quizás la introducción es algo vaga, y valga que me encanta el tenis, pero hay que reconocer que la clase de mates es muy sencilla pero currada.
Hace años que no repasaba lo que era una ecuación implícita, mira que tiempos aquellos del colegio. Y hablando de colegio y universidades, el gran engaño de la universidad, que me dicen? Quitando unas cuantas carreras, el resto está de relleno, cuantos años tirados a la basura
23 mayo 2012 | 22:40