–¿Te queda mucho, Sal?
–Sólo una multiplicación, Ven.
–¿Te puedo ayudar?
–No, gracias. Éstas no sabes hacerlas aún.
–Enséñame tú.
–Eres muy pequeño, Ven –respondió el gafotas –Ya te las enseñarán en el cole.
–Andaaaaaaa –insistía el pequeño –Enséñameee, Saaaaal…
–¿Qué es lo que quiere aprender este caballero? –preguntó Mati que acababa de llegar.
–¡Hola, Mati! –saludó Ven con alegría pensando que ella sí que le enseñaría.
–Hola, Mati –saludó Sal sin levantar la cabeza de su cuaderno –Ven quiere hacer multiplicaciones de varias cifras y aún no se lo han enseñado en el cole.
–Bueno, bueno… –comenzó a decir la pelirroja –Igual yo le puedo enseñar un pequeño truco para hacerlo…
–¿Con la calculadora? –preguntó Ven mirando de reojo.
–No, no, sin calculadora –dijo ésta –Con la mente, lápiz y papel. A ver, ¿qué multiplicación es la que queremos hacer?
–235 por 1591 –dijo Sal.
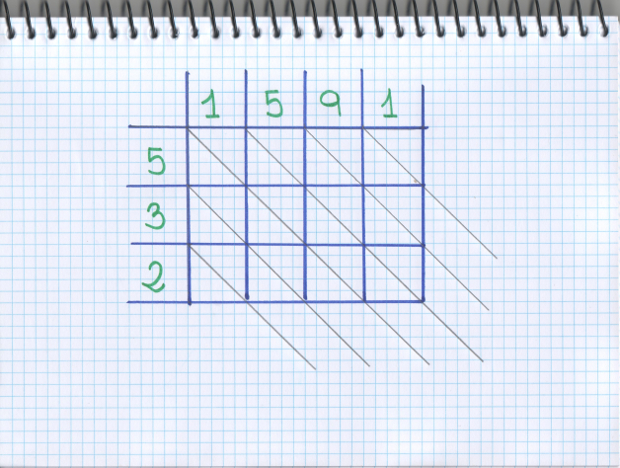
–Veréis –les dijo –Vamos a escribirlo en una tabla como en el juego de los barquitos. Ponemos arriba, en horizontal, por ejemplo, el 1591, lo escribimos de izquierda a derecha. Y en vertical, de abajo a arriba, el otro, el 235.
–Ahora vamos a dividir los cuadraditos de la tabla –les dijo –pintando estas líneas diagonales con el lápiz…
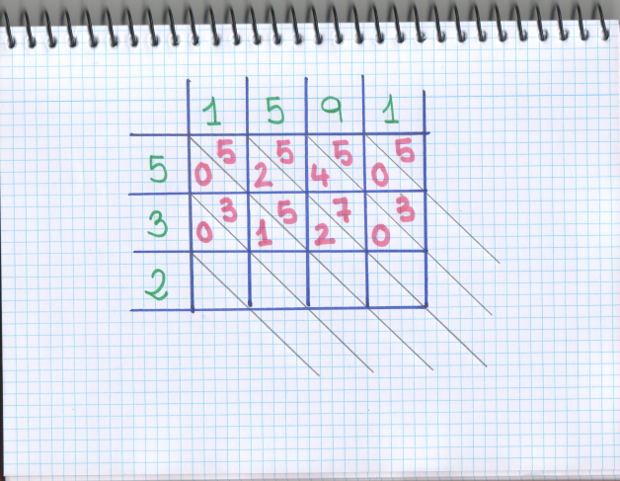
–Pues como en los barquitos –continuó Mati –Vamos rellenando los cuadraditos con el resultado de multiplicar los 2 cuadraditos correspondientes: 5 por 1 es 5, ponemos 05, para rellenar las dos mitades del cuadradito… 5 por 5 es 25, ponemos el 2 en la parte de abajo y el 5 arriba… 5 por 9 es 45, el 4 en la parte de abajo y el 5 arriba… y otra vez, 5 por 1 es 5…
–¿Puedo hacer yo el 3, Mati? Me sé la tabla del 3 –pidió el pequeño.
–Por favor… –dijo Mati y le dio el bolígrafo en una graciosa reverencia.
–A ver… 3 por 1 es 3, pongo 03, el 0 abajo… –decía Ven –3 por 5 es 15, el 1 abajo y el 5 arriba… 3 por 9 es 27, 2 abajo y 7 arriba…y 3 por 1 es 03…
–¡Me toca! –dijo Sal y su hermano le dio el boli –2 por 1 es 02… 2 por 5 es 10, el 1 abajo y el 0 arriba… 2 por 9 es 18, un 1 abajo y un 8 arriba… y otra vez 02…
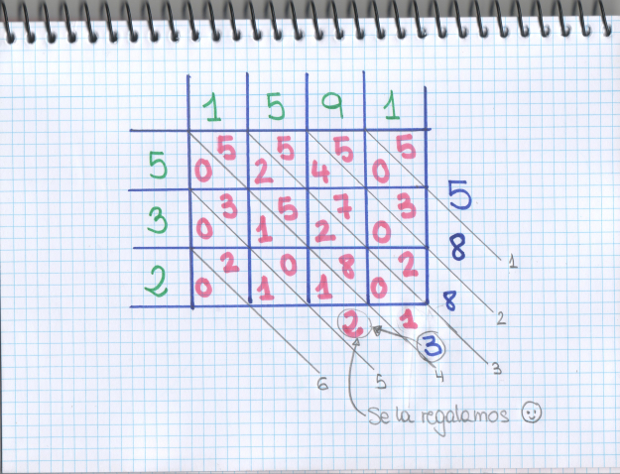
–¡Muy bien! –les dijo la gafotas –Ahora vamos a numerar las diagonales que hicimos a lápiz, empezando desde arriba, desde la más a la derecha:
–¿Y ahora qué? –preguntó el pequeño ansioso.
–Ahora vamos a sumar todos los números de color rosa que están por encima de cada diagonal, siguiendo el orden que indican los números –les dijo –Encima de la diagonal 1, tenemos solo 5, lo ponemos…
–Ahora sobre la línea 2… –empezó a decir Mati.
–¡8! –gritó Ven –5 más 0 y más 3 es ¡8!
–Eso es –confirmó Mati.
–¡Yo hago la 3! –pidió Sal — 5 más 4, es 9; más 7 es 16; más 0, nada, más 2..18 ¿lo pongo, Mati?
–No, ahora –le respondió –cuando nos sale un número de 2 cifras, ponemos sólo las de las unidades, 8 en este caso, y le regalamos las decenas a la siguiente diagonal, ¿vale?
–¡Me pido la línea 4! –exclamó Ven –¿Sumo también el 1 que le ha regalado la línea 3?
–Claro –dijo Mati –por eso lo hemos escrito en rosa.
–¡Vale! –Ven frunció el ceñó estuvo un rato mascullando y finalmente — ¡23! ¿Le regalo el 2 a la siguiente?
–Eso es –Mati sonrió satisfecha.
–Venga, ¿hacemos la 5? –les preguntó.
–La hago yo –dijo Sal –¡7!
–¡Yo termino! –pidió Ven — ¡Las dos que faltan!
–¡Qué morro! –se quejó el gafotas.
–Pero si la última es 0…
–¡Ea! –les dijo la pelirroja –Ya lo tenéis, leemos los números azules de izquierda a derecha y tenemos que 235 por 1591 es 373885.
–¡Toma, toma, toma! –gritó el pequeño — ¡Y decía Sal que era muy complicado para mí! ¡Cómo mola!
–Bueno, es cierto –aceptó el gafotas y añadió con burla –que con este método lo puede hacer un pequeñajo como tú…
Ven arrugó su carita y Sal añadió con una sonrisa
–Un pequeñajo tan listo como tú, quería decir…
Ven abrazó a su hermano sonriendo y Gauss…bueno, ya sabéis que a Gauss no le gusta demasiado quedarse al margen de estos eventos de amor desenfrenado…












Gracias por este post, muy ilustrativo. Al revés de lo que dice el tal «Pepe», se deben conocer métodos alternativos que pueden hacerle a uno la vida más sencilla. No se puede ser tan rígido.
24 octubre 2012 | 14:53
Cuando se lo explico a mis alumnos colocamos el segundo número a la derecha escrito de arriba a abajo y nos quedan las diagonales contrarias. Siempre hay alguno que se sorprende de que el resultado sea el mismo y de que no haya que pensar en las «llevadas» hasta el final. 😉
Me parece que ni pepe ni Julio ni Impeller se acuerdan de cuando aprendieron a multiplicar, ni conocen a niños que estén aprendiendo.
24 octubre 2012 | 14:58
Esto es multiplicar como toda la vida se ha hecho, sólo que torciendo las columnas (es decir, en el método ‘normal’ el 0, el 2 y el 1 de la derecha estarían uno encima del otro. Y lo que lo hace ¿más fácil? es que se apuntan las que se llevan, algo que también se puede hacer en el método tradicional. Enhorabuena, han inventado la rueda!
24 octubre 2012 | 15:08
pepe, tú si que no aportas nada.
si no eres capaz de apreciar todo lo que enseña esta historia, es que no ves mas allá de tu nariz.
24 octubre 2012 | 15:28
Igual me equivoco, pero de la manera tradicional es más sencillo explicar la propiedad distributiva de la multiplicación, tanto como el valor de un elemento dependiendo de la base…
Digamos que a,b,c,d,e,f,g € [0-9]
abcd*efg = abcd * (e * 10^2 + f * 10^1 + g * 10^0) = abcd* (e * 100 + f * 10 + g) = abcd * g + abcd * f * 10 + abcd * e * 100 siendo esta última la representación de la forma básica de resolver multiplicaciones que te enseñan en el cole: multiplicar por el número por el primer elemento, en el reglón de abajo multiplicar el número por el segundo elemento desplazado una posición (x10), en el reglón de abajo multiplicar el número por el tercer elemento desplazado una posición del anterior (x10x10 = x100), […]
Para mi, no hay nada más gráfico que la lógica, lo que pasa es que a esas edades los niños todavía no entienden de bases… No sé si es el método correcto que primero aprendan de memoria para hacer cosas que no saben y luego darles la explicación en unos años o por el contrario explicarles las reglas bajo las que se forman los números (aquello de unidades, decenas, centenas… es una buena y bonita explicación de base, para el caso concreto de base 10).
24 octubre 2012 | 15:40
madre mia… el sistema se las trae, es super efectivo, pero son como muchas cosas ¿no?
voy a practicarlo a ver que tal, aunque de momento yo lo estoy intentando hacer a la ja`ponesa, con unábaco soroban… http://miabaco.com/blog/abaco-soroban/curso-abaco-soroban
24 octubre 2012 | 15:58
Me parece normal que a Paco le parezca efectivo el sistema si está usando un ábaco… Ya puestos podría usar láminas de piedra o mármol y maza y escarpe.
Con las calculadoras esas herramientas quedaron relegadas a fines explicativos y de aprendizaje alternativo.
24 octubre 2012 | 17:03
Buen método ese… Bastante mas rápido el abaco soroban…
Quien se atreve?
Tutorial la web de miabaco…
http://miabaco.com/blog/abaco-soroban/curso-abaco-soroban#more-158
24 octubre 2012 | 19:51
Mati, ¿qué opinas de este otro método? https://www.youtube.com/watch?v=PjiIWdOPMZU Lo he encontrado hace poco por ahí y me parece menos «misterioso» que el tradicional y que este que nos cuentas.
24 octubre 2012 | 20:07
bien kastle, ya has demostrado que no sabes que es un ábaco…
25 octubre 2012 | 11:50
Yo no le veo mucha utilidad a un abaco… Mover bolas de 10 en 10 en un rollo lento
25 octubre 2012 | 20:49