Anteriormente en Mati, una profesora muy particular…
–¡Moooooooooooooola! –volvió a exclamar el pequeño.
–Sí, mola –corroboró Mati –. La recta de ecuación 2x -3y +1=0 es la gráfica de la función f(x)=(2x+1)/3.
–¿Todas las rectas son gráficas de una función, Mati? –preguntó el gafotas.
–Todas, menos las rectas verticales –dijo ella –. Basta que despejéis, en la ecuación de la recta, el valor de y y lo que os salga es la función de x que estáis representando.
–¡Toma! –exclamó Ven –¡Y lo podremos hacer también con las ecuaciones de las circunferencias!
–¡No! –dijo de pronto Mati –Las circunferencias no son la gráfica de una función, sino de 2 funciones…
–Sí, hombre… –dijo Ven desconfiado. –Piensa un poco –le retó la pelirroja –, a ver si sabes por qué. Pero ahora vamos que es la hora de la función de Sal.
En el capítulo de hoy…
–¿Nos lo cuentas, Mati? –pidió Ven con cara de no haber roto un plato en su vida.
–¿Qué queréis que os cuente, Ven? –dijo ella.
–Por qué dijiste que las circunferencias no son una función como las rectas.
–Ah, eso –exclamó Mati –. Con mucho gusto, caballeros. Os explicaré por qué las circunferencias no son la gráfica de una función.
Sal y Ven sacaron su cuaderno dispuestos a escuchar la explicación de Mati. Gauss no parecía demasiado interesado, la verdad.
–Como os dije la otra tarde –comenzó a decir la pelirroja –, una función es una regla o ley que te permite asignar a cada elemento de un primer conjunto un único elemento de otro conjunto.
–¿Y? –preguntó el gafotas.
–Cuando tenemos una recta, los puntos sobre el eje horizontal, el de abscisas, os lo conté cuando explicamos coordenadas cartesianas, son elementos del primer conjunto –les dijo –, y la función, cuya gráfica está representada por dicha recta, asigna a cada punto del eje de abscisas, o mejor dicho, al valor que representa, la segunda coordenada del único punto sobre la recta que tiene como primera coordenada dicho valor en la abscisa.
Los niños arrugaron sus caritas como pasas. Gauss ladró bajito haciéndose el interesante.
–¿Lo vemos con un ejemplo? –preguntó Mati.
–Por favor –dijo Sal.
–Vamos a dibujar en nuestros ejes coordenados la recta de ecuación y=2x + 1 –dijo Mati –, que es la gráfica de la función f(x)=2x+1. Para ello solo necesitamos dar 2 valores a x, porque por 2 puntos pasa una única recta. Para x igual a 0, y será 2 por 0 más 1, o sea 1. La recta pasa por el punto (0,1). Para x igual a 1, y será igual a 2 por 1, 2, más 1, o sea 3, la recta pasa por el punto (1, 3).
–Ahora, ya veréis como a cada punto del eje de abscisas –continuó Mati –solo le corresponde un valor de la función f(x)= 2x + 1. Decidme un número.
–¡El 4! –gritó Ven.
–Para calcular el valor que nuestra función asocia al número 4 –dijo ella –o bien sustituimos x por 4 en la función, o bien, trazamos una recta vertical sobre el 4 del eje de abscisas.
–Pintamos la recta vertical que pasa por el 4 –dijo Mati –que en realidad es el punto (4,0) del plano. Esta recta vertical será la recta de ecuación x=4 y vamos a ver cómo sólo corta a nuestra función, la recta verde. en un único punto:
–La corta en el punto (4, 9) –dijo Sal.
–Y sólo en el (4, 9) –añadió Mati –. Eso significa que f(4)=9, es decir, que la función asocia al 4 el valor 9.
–¡Toma, toma, toma! ¡Cómo mola! –exclamó Ven.
–Vamos a ver ahora qué pasa con la circunferencia –les propuso Mati –. Decidme el centro y el radio.
–El centro será el (0,0) –dijo de repente el pequeño.
–Y de radio 5 –añadió el gafotas.
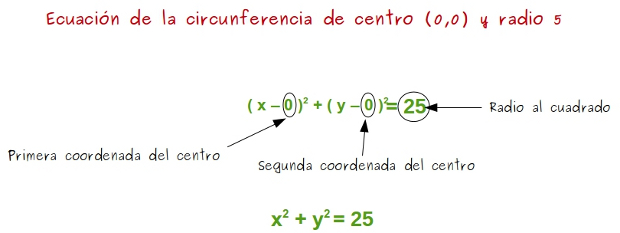
–Vamos a calcular su ecuación como os enseñé –les propuso ella.
–La ecuación es x2 + y2= 25 –dijo Sal.
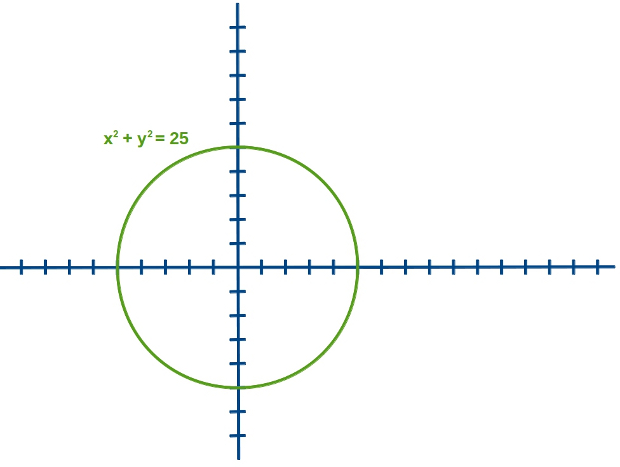
–Ahora la dibujamos en nuestros ejes coordenados –dijo ella.
–Veréis qué pasa si quisiéramos calcular la imagen del 2 –propuso Mati –en la función cuya gráfica es la circunferencia verde. Para ello, como antes, dibujamos la recta vertical sobre el 2, la recta de ecuación x=2.
–¡Toma, toma, toma! ¡Es verdad! –gritó Ven –¡Es verdad!
–¿Y por qué pasa eso? –quiso saber el gafotas.
–Pues verás –empezó diciendo ella –, si despejamos y en la ecuación de la circunferencia nos queda:
–Pero, Mati –dijo Sal –, has conseguido despejar y en la ecuación, entonces ¡es una función!
–No –respondió esta –, porque no da un único valor para cada x…
–¡Anda que no! –dijo Ven.
–Pues no –dijo Mati respondona –¿Cuánto vale la raíz cuadrada de 4?
–¡2! –dijo Sal con entusiasmo.
–O -2 –añadió la pelirroja –Porque -2 al cuadrado también es 4.
–Ah, claro –reconoció el gafotas.
–Si en la ecuación de la circunferencia –continuó ella –sustituimos x por 4, ¿qué ocurre?
–¡Tooooooooooooomaaaaaaaaaaa! –gritó Ven.
–Por eso –dijo Mati –, cuando aparece la raíz cuadrada ponemos delante +√9, -√9 o, incluso ±√9, si queremos indicar que consideramos los 2 posibles valores de la raíz cuadrada.
–Ajá –asintió el gafotas, mientras su hermano seguía mirando el dibujo de la circunferencia de centro (0,0) y radio 5 que habían dibujado en el cuaderno.
–¡Qué pena! –dijo –Tan redondita y no es una función…









Claro, yo sigo la definición de Goursat y no la de Patrick Suples
De esta manera yo admito el concepto «clásico» de función y Patrick Suples y tú no.
De manera que Goursat y yo admitimos el concepto de función de Descartes, Leibnitz, etc. y Patrick Suples y tú no.
Para mí Patrick Suples define el concepto de aplicación que yo admito pero como «aplicación». Para Goursat y para mí el concepto de función es más amplio que el de aplicación.
No veo dónde me quitan la razón, es lo que vengo diciendo desde mi primera intervención: «En esta publicación se confunde APLICACIÓN con FUNCIÓN. Todo lo que se dice se refiere a aplicaciones, no a funciones.»
10 marzo 2013 | 23:16
¡Ah, eres tu! Me habían dicho que había uno que todavía seguía esa definición. Bueno, ahora lo entiendo. Buena suerte a la hora de entenderte con los demás matemáticos con título.
11 marzo 2013 | 9:26
“Matemático…”:
Dices que tú sigues la definición de Goursat (por cierto, de los años veinte, anterior a Gödell: repasa lo que has dicho en tus anteriores comentarios), haciendo una lectura muy relajada de la frase (copio literalmente «Se dice que y es una función de x si a cada valor de x le corresponde UN valor de y»,pero NO ES CIERTO, porque, para tu mala suerte, el libro de Goursat está online (en su traducción al inglés) http://archive.org/stream/coursemathanalys01gourrich#page/n17/mode/2up y copio literalmente:
“Let this variable denoted by x, and let us suppose, for example, that it can assume all values between two given numbers a and b (a<b). Let y be another variable, such that to each value of x between a and b, and also for the values of a and b themselves, ther correspond ONE definitely determined value of y, them y is called a function of x".
Después sigue explicando tu amigo Goursat (que parece que te ha abandonado), que se puede ver también gráficamente una función como "a curvilinear arc of any shape, which is not cut IN MORE THAN ONE POINT by any parallel to the axis Oy".
Así que no hay ni una sola definición, ni una sola, que admita que cada elemento del dominio tenga más de un valor de la imagen (desde luego no la de Goursat). No hay ni una definición, ni una sola, que diga que una función es cualquier subconjunto del producto cartesiano. Lo que sí que hay gente que no sabe leer ni reconocer que se han equivocado.
Así que Gousart y todas, TODAS las referencias que tú has citado y todas las que hemos citado los demás te quitan la razón.
Realmente ya hemos perdido demasiado el tiempo contigo, si lo hemos hecho así no es por nuestro gusto sino porque no nos parece razonable (hablo al menos por mi) que en un producto tan bien explicado (que seguro que tiene sus errores) y que una labor tan loable como la de Clara Grima y Raquel Garcia Ulldemolins quede manchada por comentarios tan negativos y erróneos como el tuyo. Dije que me retiraba de la discusión y no lo he hecho puesto que he visto que persistías en tu error (ya te hemos dicho más de uno que parece que tienes la santa costumbre de no leer las cosas hasta el final). Así que por favor, si vas a dar una definición de función (te ahorro el tiempo: no existe) que apoye tu tesis: cita la fuente y copia hasta el final.
Pero como resumen: "Matemático…" dijo que en esta entrada se confundía el concepto de función (un problema de definición, no se decía que hubiera ningún fallo lógico a partir de la definición aquí dada), hemos dado multitud de referencias de los libros de matemáticas más aceptados, de los autores más prestigiosos que dan la misma definición (o equivalente) a la aquí dada. "Matemático…" ha ido dando autores que según él seguían su definición: si leemos los textos de esos autores que él cita, ninguno de dichos autores daba la definición de él, sino la aquí considerada. Me parece que "Matemático…" va por una autopista y todos los demás van conduciendo en sentido contrario salvo él. Así que debería haber puesto:
"en esta publicación Y EN TODAS LAS DEMÁS PUBLICACIONES DE MATEMÁTICOS DE PRESTIGIO QUE HEMOS ENCONTRADO SIN NINGUNA EXCEPCIÓN se confunde aplicación con función".
11 marzo 2013 | 10:28
La cita de Goursat no es mía, no, es de:
Artículo de: J J O’Connor y E F Robertson
MacTutor History of Mathematics Archive
Sigamos pues, copio de la Wikipedia
En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir, F ′ = f.
Dado que la derivada de una constante es cero, tendremos que cos(x) tendrá un número INFINITO de primitivas tales como sin(x), sin(x) + 5, sin(x) – 100, etc. Es más, cualquier primitiva de la función f(x) = cos(x) será de la forma sin(x) + C donde C es una constante conocida como constante de integración.
A ver como me casas la definición «con unicidad» que se da en muchas publicaciones, con este número INFINITO de primitivas.
Es decir a una única función del dominio le corresponden infinitas funciones en la imagen.
La definición que exponen estos autores que citas, es claramente inconsistente y no se puede admitir en Matemática «Formal», aunque ya sé que no es culpa tuya y hay muchos autores que siguen esa definición.
Esta inconsistencia se resuelve distinguiendo entre aplicación y función.
Nota: cos(x), sin(x) se puede sustituir por otra función y me refiero a Integrales indefinidas, funciones inversas de las derivadas.
12 marzo 2013 | 1:09
Dame una definición, solo una, de función donde diga: «definimos una función como un subconjunto cualquiera del producto cartesiano», aunque sea en un libro rumano de mediados del siglo XIX, ya sé que todos los libros que hemos consultados están equivocados, aunque también sé que no sabes leer muy bien puesto que la cita de MacTutor no decía (ya te lo dijeron) lo que tú dices y la de la wikipedia que ahora citas tampoco sirve para defender tu postura (por cierto: me encanta que ahora la wikipedia sí sea válida): vuelve a leer la cita que pones porque lo que hace es situarse en nuestro terreno.
Te copio:
«En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir, F ′ = f.» (<- evidentemente no está en contradicción con la definción que da TODO el mundo de función, pero por si a alguien le queda dudas la wikipedia aclara:
"Dado que la derivada de una constante es cero, tendremos que cos(x) tendrá un número INFINITO de primitivas" Luego la función primitiva no es única, para cada función le corresponde un número infinito de funciones primitivas y después sigue con lo mismo.
Repito: no trates de encontrar la inconsistencia de todas las matemáticas para justificar tu postura, estábamos hablando de definiciones, tú decías que la definición aquí dada casi no se utiliza desde los años 30 (lee tus comentarios), por lo tanto te debe ser muy fácil (mucho más que probar la inconsistencia del resto de los matemáticos) encontrar un único sitio donde dé tu definición de función.
Por otra parte te repito: no mereces la pena: tu postura es ridícula, te hemos citado todos los autores habidos y por haber que dan siempre la misma definición de función (todos equivocados). Demuestras en cada texto que pones que no sabes leer bien las matemáticas que en él se exponen. La única razón por la que sigo es porque no quiero que en una entrada tan fantástica como esta, en un blog que tanto bien está haciendo por la difusión de las matemáticas quede tu palabra como la última.
12 marzo 2013 | 9:47
http://www.cs.unicam.it/piergallini/home/materiale/geom4/testi/Spivak:Calculus%20on%20manifolds.pdf
Desde aqui se tiene acceso al libro «Calculus on Manifolds» A Modem Approach to Classical Theorems of Advanced Calculus, escrito por Michael Spivak
En la página 11 se lee:
A function from Rn to Rm is a rule which associates to each point in Rn some point in Rm
Es decir, a un punto del dominio se le asocia algún punto del rango (no dice que sea único)
En la página 23 se lee:
f(x,y,z) = (x + y)^z, si z=2 ,(x + y)^2 es una función, luego x^2+y^2+2xy es una función, luego x^2+y^2 es una función
En la página 27 se lee:
f(x,y) = x^2 – y^2, luego x^2+y^2 es una función
En la página 40 se lee:
Consider the function f: defined by f(x,y) = x^2+y^2-1, luego x^2+y^2 es una función
y así un larguísimo etc.
El carácter riguroso, matemáticamente hablando, de este libro queda claramente reflejado en la página 45.
Conclusión, x^2+y^2 es una función, según enseñaba, Michael Spivak en la
Brandeis University, y según el libro «Calculus on Manifolds» A Modem Approach to Classical Theorems of Advanced Calculus, contrariamente al título del articulo que ha originado este debate.
17 marzo 2013 | 1:41
O no sabes leer o eres un mentiroso o no tienes ni idea de matemáticas («o» no excluyentes).
«Some point» es singular, en inglés si quieres decir varios puntos tendrías que decir «some pointS», pero Spivak aclara:
Página 11 del Spivak (en la misma referencia que tú das), justo después de lo que tu copias y para aclarar la definición por si alguien es tan lerdo y no se entera:
«THE point a function associates to x IS denoted f(x)» luego según la referencia que das la función asocia a cada punto del dominio una ÚNICA imagen (justo después vuelve a poner f(x) pertenece a R^m (pertenece: no incluido) por si todavía alguien no se ha enterado (como es tu caso).
Naturalmente que f(x)=x^2+y^2 (y todos los demás ejemplos que das) es una función, en este caso de R^2 en R y asigna a cada valor de (x,y) UN ÚNICO valor de z tal y como se dice en esta entrada, tal y como se te ha dicho repetidas veces, tal y como viene en TODAS las referencias que te hemos dado y que tú has dado.
Me alegro que digas que la referencia del Spivak es rigurosa, porque te quita totalmente (y repetidas veces) a razón.
Repito: a cada valor del dominio le corresponde UN ÚNICO valor de la imagen y o das una referencia donde diga claramente que considera una función cualquier subconjunto del producto cartesiano o deja de hacer el ridículo y hacer perder el tiempo a los demás.
Un
17 marzo 2013 | 12:23
Conclusión, x^2+y^2 es una función, según enseñaba, Michael Spivak en la
Brandeis University, y según el libro “Calculus on Manifolds” A Modem Approach to Classical Theorems of Advanced Calculus, contrariamente al título del articulo que ha originado este debate.
http://www.cs.unicam.it/piergallini/home/materiale/geom4/testi/Spivak:Calculus%20on%20manifolds.pdf
17 marzo 2013 | 16:12
¡¡¡¡¡Aprende a leer!!!!!
Conclusión: f(x,y)=x^2+y^2 es una función de R^2 en R siguiendo la definición que se da en esta entrada: a cada valor de (x,y) le corresponde UN UNICO valor f(x,y).
Spivak dice claramente que a cada valor del dominio le corresponde UN ÚNICO valor de la imagen (y lo repite hasta tres veces en tu famosa página 11 de dicho libro).
17 marzo 2013 | 16:48
Leo los comentarios a esta entrada y me alarmo ante la paciencia que Alberto demuestra ante la ignorancia y el empecinamiento de «Matemático, según un título que tengo…».
No sé dónde le dieron el título de matemático, pero espero que no lo diga: no hace falta desprestigiar más a las universidades españolas.
Si le sirve de algo, solo decir que los comentarios de «Matemático, según un título que tengo…» producen verdadera vergüenza ajena, parece que no ha leído ni uno solo de las respuestas que se le dan por parte de Alberto y de «Profesor de matemáticas, según dicen en mi universidad», este último, con toda la razón del mundo ya se cansó ante tanta tontería. El último comentario ya es tremendo: claro que f(x,y)=x^2+y^2 es una función, ya que a cada valor (x,y) del dominio le asigna un único valor x^2+y^2 (de la imagen).
Lo dicho: me da vergüenza que alguien que se diga matemático no sea capaz de comprender definiciones tan elementales.
Por supuesto me uno a las muchas felicitaciones por la labor llevada a cabo en este blog y os animo a seguir adelante.
17 marzo 2013 | 17:00
Una cosa más: si f(x,y)=x^2+y^2 no es una función según la definición dada en esta entrada, significa que para algún valor de (x,y) le corresponde más de un valor de f(x,y), ¿me podrías dar un ejemplo de un solo valor de (x,y) al que le correspondan más de un valor de f(x,y)=x^2+y^2?
17 marzo 2013 | 17:04
Conclusión, x^2+y^2 es una función, contrariamente al título del articulo que ha originado este debate.
http://www.cs.unicam.it/piergallini/home/materiale/geom4/testi/Spivak:Calculus%20on%20manifolds.pdf
17 marzo 2013 | 22:21
Somos muchos…
18 marzo 2013 | 0:41
Repito: aprende a leer, es terrible que no sabes leer lo que se pone en la entrada (NUNCA se afirma que f(x,y)=x^2+y^2 no sea una función), ni lo que pone los libros que citas, que dicen repetidas veces que no tienes razón en tu definición de función).
Tal y como dice 3 VECES Spivak: a cada valor del dominio le corresponde un único valor de la imagen tal y como dice la entrada y como tú te has negado a ver desde el primer momento. Por lo tanto en la entrada se dice que f(x,y)= x^2+y^2 es una función: léelo al menos una vez.
Por favor responde a estos puntos:
1) Has dicho que la definición correcta de función era «cualquier subconjunto del producto cartesiano». Da una sola cita en la que se de esa definición.
2) en el libro de Spivak se dice 3 veces en la página en la que se da la definición de función que a cada valor del dominio le corresponde un único valor de la imagen: 3 veces en unba página te dice la cita que tú das que estás equivocado.
3) Dime dónde se dice en la entrada que f(x,y)=x^2+y^2 no es una función.
4) en la entrada y en todas las definiciones que has encontrado se dice que a cada valor del dominio le corresponde un único valor de la imagen, si dices que con la definición dada en la entrada f(x,y)=x^2+y^2 no es una función, es porque para algún valor de (x,y) le corresponde más de un valor de f(x,y)=x^2+y^2 , ¿me puedes decir un valor de (x,y) de x^2+y^2?
Un último consejo: no leas tus comentarios: te darán vergüenza.
18 marzo 2013 | 10:35
Señorita Mati, respetuosamente, considere la ecuación paramétrica de su circunferencia
x = 5·cos(α)
y = 5·sen(α)
con α ∈ [0, 2π]
Para cada valor de α le corresponde un único punto (x,y) del plano y se evita el problema de los signos de la raíz.
Con esta notación su circunferencia es una función. Usted se equivocó.
19 marzo 2013 | 15:29
una cuestión es la gráfica como objeto en el plano y otra las infinitas parametrizaciones que la representan. Por ejemplo x= 5 cos(t*t), y= sen(t*t), t en [0, raíz(2 pi)] daría el mismo problema.
21 marzo 2013 | 6:49