¿Cuál es el camino más corto a las Islas Salomón?

Imagínense que por alguna razón quieren viajar a las Islas Salomón.  No sé, igual conocemos a más gente de allí de la que pensamos, yo qué sé… ¿Cuál creen ustedes que sería la ruta más corta para volar hasta el Aeropuerto Internacional de Guadalcanal, por ejemplo? Puede que alguien tuviese la tentación de tomar el mapamundi y una regla y dibujar la línea recta que une Sevilla, que es de donde yo saldría,  con Guadalcanal, por aquello que heredamos de Euclides de que la distancia más corta es una línea recta.  Cosa que es cierta si nos movemos en un plano  y medimos con la distancia euclídea. Medir con la distancia euclídea no es más que lo que hacemos cuando usamos una regla o una cinta métrica, medir la longitud del segmento que une a los dos puntos en el plano.

Ahora bien, si nos vamos a mover de un punto a otro del planeta, nos estamos moviendo, no sobre un plano, sino sobre una esfera. Ya, ya sé que la tierra no es una esfera, pero se le falta muy poquito, ¿no? Pero venga, vamos a pensar en una esfera, que no tiene por qué ser la Tierra, y vamos a ver cómo se calcula el recorrido más corto entre dos puntos sobre ella.

La línea más corta entre dos puntos de la esfera es la geodésica. «Muy bien, Mati,  ¿y qué es una geodésica?» Pues la geodésica que une a dos puntos sobre la esfera, es la curva que se dibuja sobre la esfera si la cortamos con un plano que pase por los dos puntos escogidos y el centro de la esfera. Es decir, que las geodésicas son arcos sobre las esfera, correspondientes a círculos que estarían centrados en el centro de ésta. Vamos, que si pensamos en la esfera terrestre, por ejemplo, los meridianos (que nos permiten medir la longitud) son geodésicas, puesto que  son círculos que estarían centrados en el centro de la esfera; mientras que los paralelos (que nos permiten medir la latitud) no lo serán, porque (salvo el ecuador) el círculo que los definen no está centrado en el centro de la esfera.

Antiguamente, era relativamente fácil saber a qué distancia sobre el ecuador (latitud) nos encontrábamos (midiendo la altura del sol o algunas estrellas sobre el horizonte), pero para determinar la posición exacta sobre la Tierra era necesario conocer otra coordenada, normalmente la longitud.  El problema de determinar la longitud no se resolvió (gracias al desarrollo de relojes más precisos que los existentes hasta su momento, por parte de John Harrison a mediados del siglo XVIII). Por lo tanto cuando un descubridor se internaba en un océano desconocido como Colón en 1492 se solía seguir no el camino más corto, la geodésica, (para determinarlo sobre la esfera es necesario conocer el punto de partida y el punto de llegada) sino que se navegaba siguiendo algún paralelo. Esto, las corrientes marinas y que no le hicieran caso en Portugal (su primera intención) fue muy importante para el éxito del primer viaje de Colón. Por aquel entonces, la hegemonía de las exploraciones correspondía a la corona portuguesa. Y Portugal había lanzado varias expediciones (Fernão Teles en 1475 y Ferdinand van Olm en 1486).

¿Qué problema encontraron dichas expediciones? Pues que si querían viajar hacia el oeste siguiendo el paralelo y como partían del lugar más lógico para ellos: el punto más occidental dominado por la corona portuguesa: las islas Azores, se encontraban de frente la fortísima corriente del Golfo (y los vientos que la acompañan) lo cual dificultaba tremendamente la navegación y hacía casi imposible avanzar. Colón tuvo la suerte de no ser aceptado por lo portugueses y tuvo que ir a pedir la ayuda a la corona de Castilla, que, al concedérsela, le exigió que debería partir de puerto castellano, por lo tanto, la última tierra conocida que visitaron fueron la islas Canarias (La Gomera y Gran Canaria). Desde las Canarias las corrientes y los vientos apuntan hacia el oeste y permitieron su viaje. De hecho, en el viaje de vuelta la ruta escogida por Colón fue mucho más al norte y así estuvo ayudado por la corriente del golfo que lo empujaba hacia Europa.

Dejando a un lado antiguas rivalidades con nuestros vecinos lusos, que no quiero que nadie piense que estoy haciendo patria ante el inminente encuentro en semifinales de la Eurocopa, y volviendo a nuestros planes de volar a las Islas Salomón, alguien podría caer en la tentación de pensar que la ruta que seguiríamos en el vuelo corresponde con la línea recta que une el origen con el destino con una línea recta sobre el mapa. Pero esto no es así, porque los vuelos de los aviones suelen seguir, salvo algunas restricciones,  la ruta marcada por el arco de geodésica que une el aeropuerto de origen con el aeropuerto de destino. Y como veis en la siguiente imagen, en el caso de un vuelo desde Sevilla al aeropuerto internacional de Honiara, la ruta está bastante alejada de esa línea recta.

Imagen creada en http://www.gcmap.com

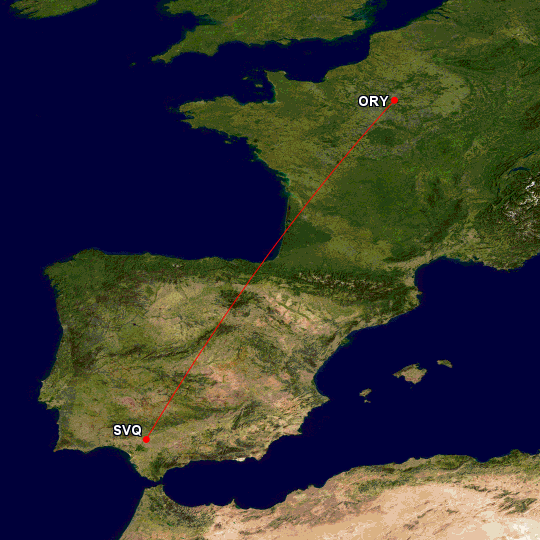
La diferencia entre la ruta marcada por la geodésica y la que nos proporcionaría la línea recta es más acusada cuanto más largo sea el vuelo y cuanto más diferencia de latitud haya entre los dos puntos. Vean si no, por ejemplo, la geodésica entre Sevilla y París.

Como ya he dicho antes, no es que los aviones sigan exactamente la ruta de la geodésica, porque ésta puede incluir zonas sobre las que no es posible volar por cuestiones geográficas y/o metereológicas, o incluso normativas internacionales de restricciones de tráfico aéreo. Pero no me digan que no les sorprende ver sobre el mapa cuál es la distancia más corta hasta las Islas Salomón… y quién sabe, a lo mejor, tenemos que darnos un paseo por allí.

Tags: esfera, geodésicas, latitud, longitud, meridianos, paralelos | Almacenado en: Ahora que los niños salieron a jugar...