–¡Cara! ¡Saco yo!
–¡No vale! ¡Ha rebotado en Gauss! –Ven estaba un poco mosqueado.
–¿Otra vez? ¿Y eso qué más da, Ven?
–Se repite. Ah, se siente…
–¡Cara! ¡Saco yo! –gritó Sal de nuevo.
–No, no vale –respondió Ven, mientras Gauss resoplaba con cansancio.
–Y ahora, ¿qué pasa? –protestó el gafotas.
–No me fío de esa moneda, la has cogido de tu hucha…
–Vamos, Ven –bufó Sal –No tengo ninguna moneda falsa en mi hucha…
–¿Cómo lo sabes? –inquirió el pequeño –¿Los has comprobado como nos enseñó Mati?
–No, no lo he comprobado, Ven –respondió Sal aburrido –Pero son todas verdaderas, como las tuyas…
–¿Qué les pasa a estos chicos? –Mati acababa de llegar.
–Hola, Mati –la saludó Sal.
–Hola, Sal me quiere hacer trampa con la moneda –dijo el pequeño.
–Pesado… –bufó Sal.
–¿Por qué crees que Sal te quiere hacer trampas, Ven?
–Porque ha traído una moneda que siempre sale cara… –contestó éste.
–Eso no es verdad, Ven –se defendió Sal –Ha sido casualidad.
–Vamos a ver –intentó mediar Mati –¿Queréis que os cuente algo sobre lanzamientos de monedas y probabilidad?
–¡Sí! –contestaron los dos a la vez. Gauss resopló aliviado. Mati sacó su libreta.
–Vamos a aprender primero cómo se calcula la probabilidad de que salga cara en la moneda usando la regla de Laplace –comenzó a contarles la pelirroja.
–En el caso del lanzamiento de una moneda y calcular la probabilidad de obtener cara –siguió –el número de casos favorables es 1, que salga cara, y el número de casos posibles es 2, cara y cruz.
–Y sale 1/2 –dijo Ven –La mitad, eso ya lo sabíamos, Mati, el 50% de posibilidades…
–Sí, lo sé –afirmó ella –Con las monedas es muy fácil, pero sirve para todo. Por ejemplo, si lanzamos un dado, ¿cuál es la probabilidad de obtener una potencia de 2?
–Yo lo hago en la libreta, Mati –se apresuró a decir Sal
–Sí, pero ¿por qué no calculas la probabilidad de que Sal saque cuatro caras seguidas? –pidió Ven a la pelirroja.
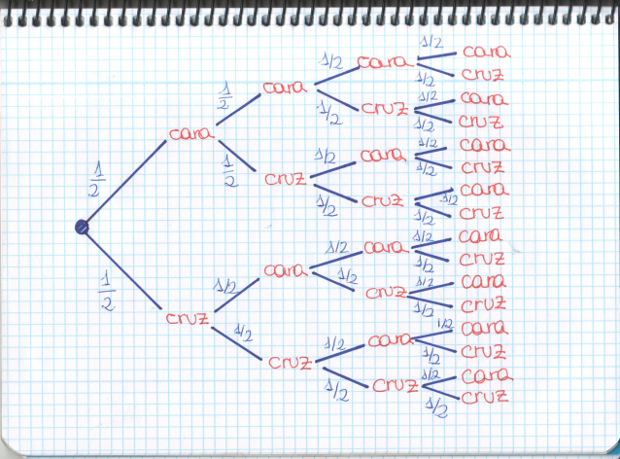
–Vale, vamos a hacer un diagrama con todas los posibles resultados del lanzamiento de una moneda 4 veces –les dijo.
–Si empezamos en el punto azul y caminamos sobre las aristas azules, tenemos todos los resultados, ¿no?
–A ver… –dijo Ven señalando con su dedo sobre el diagrama —Cara, cruz, cruz, cruz… Y por aquí, cruz, cara, cara, cara...
–Si, Ven –interrumpió su hermano –Están todas.
–Ahora bien, en cada tirada, la probabilidad de obtener cara o cruz es siempre 1/2, ¿no? –continuó ella –Lo escribimos sobre las ramas.
–Bueno, chicos, ¿cuántos casos posibles hay? –preguntó Mati –Sólo tenéis que contar la columna de la derecha, cada una corresponde a un resultado posible.
–¡16! –dijo Ven con entusiasmo.
–¿Y caso favorables para obtener 4 caras? –siguió preguntando la pelirroja.
Los niños estuvieron mirando el cuaderno…
–Sólo uno, Mati –señaló Sal — Sólo cuando sale cara, cara, cara, cara.
–Entonces la probabilidad de obtener 4 caras es… –Mati dejaba la pregunta en el aire.
–¡1/16! –dijeron los 2 hermanos a la vez.
–Efectivamente, chicos –corroboró Mati –Y si os fijáis, 1/16 es el resultado de multiplicar las probabilidades que nos vamos encontrando por el camino hasta llegar al cuarto lanzamiento…
–Es verdad –dijo Sal con alegría.
–Pero Mati –intervino Ven –Cuando sean 20 tiradas, nos va a salir un diagrama, ¡enorme!
–Tienes razón, pero no hace falta hacer el diagrama –aceptó Mati –Se trata de calcular la probabilidad de una intersección de sucesos independientes, porque el resultado de cada lanzamiento es independiente del anterior. Un suceso es que la primera salga cara, otro que la segunda salga cara, el tercero que salga cara en la tercera y el cuarto, que la cuarta tirada dé cara. Cada uno de estos sucesos, tiene probabilidad 1/2, como hemos dicho, ¿verdad? Eso significa que en cada tirada de las 4, la probabilidad de que salga cara es 1/2 o sea, de un 50%.
–Ahora bien, la probabilidad de que las cuatro veces nos salga cara es la probabilidad de la intersección, y eso se calcula sabiendo que, como son independientes, la probabilidad de la intersección es igual al producto de las probabilidades.
–¿Ves, Mati? –dijo Ven con vehemencia –Es casi imposible que pase, y ha pasado
–Tú lo has dicho, Ven –dijo ella –casi imposible, pero no imposible.
–¡Que mi moneda es buena, de verdad! –se quejó Sal.
–A ver, Ven –dijo la pelirroja –Si hacemos otra vez el sorteo, ¿tú que pedirías, cara o cruz?
El pequeño se quedó un rato pensando, al cabo del cual contestó:
—Cruz.
–¿¿Cruz?? –preguntó Sal sorprendido –¿No decías que en mi moneda sólo sale cara?
–Ya… -dijo Ven mirando al suelo –Pero en realidad, creo que tu moneda es auténtica y como ya han salido 4 caras… toca cruz.
–Huy, creo que Ven ha caído en la falacia del jugador… –dijo Mati con voz misteriosa.
–¿La qué? –preguntó Sal con los ojos de par en par.
–Una falacia es una mentira o engaño –empezó a explicarles –La falacia del jugador, o falacia de Montecarlo, es la falsa creencia de que lo sucedido anteriormente en un experimento aleatorio, al azar, afectará al resultado de los experimentos siguientes.
–No entiendo nada de nada… –confesó Ven.
–Es lo que tú acabas de hacer, Ven –continuó ella –Crees que el hecho de que hayan salido ya 4 veces caras, afectará al 5º lanzamiento y no es verdad. La probabilidad de obtener cruz en el 5º lanzamiento es, de nuevo, 1/2, como siempre.
–Claro… Qué tontería…
–Bueno, Ven, esa tontería como tú la llamas, engaña a mucha gente que piensa que si sale varias 4 veces seguida cara, lo lógico es apostar a cruz por que ya toca. Y no, están confundiendo la probabilidad de obtener 5 caras seguidas con la probabilidad de obtener cara en el 5º lanzamiento.
–¡Toma, toma, toma! ¡Es verdad! –el pequeño estaba alucinando.
–Cuando lo lógico sería lo contrario –siguió la pelirroja.
–¿Lo contrario? ¿Por qué, Mati? Si cara y cruz tienen la misma probabilidad –el gafotas estaba muy intrigado.
–Ya, pero si sale muchas veces seguida cara –siguió ésta –lo que parece indicar es que la monedad no está bien compensada y que, por lo tanto, tiene más probabilidad de salir cara.
–Cierto… -se quedó pensando Sal –Si la moneda es buena, no importa lo que ha pasado antes.
–Eso es, Sal, en ese caso decimos que son experimentos independientes –confirmó la gafotas –El resultado de un experimento no depende del anterior.
–¿Y hay experimento dependientes? –preguntó Sal de nuevo.
–Sí, naturalmente –dijo Mati –Por ejemplo, si tenemos 5 bolas rojas y 3 bolas verdes en una bolsa, ¿cuál es la probabilidad de meter la mano y sin mirar sacar una bola roja?
Los niños se quedaron pensando.
–5/8 –dijo Sal
–Muy bien –sonrió Mati — La dejamos fuera ¿Y la probabilidad de que la segunda sea roja?
Sal y Ven montaron de nuevo su gabinete de resolución de problemas.
–Un momento, Mati –preguntó el pequeño –La primera que sacamos fue roja, ¿no?
–Me alegro de que me hagas esa pregunta –respondió Mati haciéndose la interesante –Eso significa que el resultado del segundo experimento depende del primero, ¿no? Son experimentos dependientes.
–¡Claro! –la carita de Sal brillaba con alegría –¿Cómo se calcula entonces, Mati?
–Vamos a verlo en el cuaderno –propuso Mati –Lo que queremos conocer es la probabilidad de que en la segunda extracción (ya hay una bola fuera) saquemos una bola roja. A esa probabilidad que queremos calcular la llamaremos P(2ªR). Para calcular P(2ªR) vamos a necesitar calcular otras probabilidades antes. Por ejemplo, la probabilidad de que la 2ª bola sea roja condicionada al hecho de que la primera que salió fuese roja, lo llamamos P(2ªR | 1ªR)
–De la misma manera, necesitaremos conocer la probabilidad de que la segunda bola sea roja condicionada al hecho contrario, es decir, al hecho de que la primera no fuese roja.
–Por último, necesitaremos usar la probabilidad de que la 1ª bola extraída fuese roja y la del suceso contrario, la de que la 1ª bola no fuese roja.
–Con todo esto, ya podemos calcular la probabilidad de que la segunda vez, extraigamos una bola roja, o sea, P(2ªR), usando esta fórmula
–Ya sólo –dijo Mati –necesitamos calcular esos 4 términos para conseguir lo que queremos ¿Me ayudáis?
–¡Sí! –dijeron los niños al unísono.
–Empezamos por la probabilidad de que la 2ª bola sea roja sabiendo que ya sacamos una y que fue roja –les dijo.
–A ver… –comenzó hablando Sal –casos posibles son 7 porque ya hay una bola menos…y casos favorables, serán 4 porque había 5 bolas rojas pero ya sacamos 1.
–¡Muy bien! ..les animó Mati –Ahora la otra condicionada, la probabilidad de que la segunda sea roja sabiendo que la primera que sacamos no lo era.
–Me toca –dijo Ven animado –Caso posibles son 7, claro, y casos favorables… 5, las 5 bolas rojas.
–Pero bueno…-Mati sonreía orgullosa –Lo que queda ya lo tenéis muy fácil
Los niños terminaron de calcular los términos que le faltaban
–¡Perfecto! –dijo la pelirroja –Ya lo tenemos todo
–¡Toma, toma, toma! –el pequeño Ven estaba alucinando.
–Me encanta, Mati –añadió el gafotas.
–Me alegro –dijo ella –El cálculo de probabilidades es muy entretenido y sencillo. Con esto y con un poco de observación, una familia española, los Pelayo, ganaron mucho dinero. Pero a vosotros todavía no os interesa el dinero, ¿verdad?
–No, ¡nos interesa el fútbol! –dijo Ven.
–Bueno, y las matemáticas –añadió Sal con una sonrisa.
—Volviendo al asunto del fútbol –empezó a decir Mati –si queréis, por ejemplo, elegir campo en el fútbol y no estáis seguros de que la moneda esté equilibrada, os enseñaré a hacer un sorteo justo.
—¿Cómo? —preguntó casi gritando Sal sonriendo esperando la respuesta de Mati.
—Muy fácil, haciendo el sorteo a dos tiradas –propuso ella –La moneda será lanzada dos veces, y los jugadores elegirán sólo entre dos posibilidades: (cara, cruz) y (cruz,cara). Si las dos veces la moneda saca lo mismo, es decir (cara, cara) o (cruz, cruz), repetimos los dos lanzamientos. Pero los dos sucesos (cara, cruz) y (cruz, cara) tienen la misma probabilidad de salir. Nadie puede enfadarse.
–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven –Vamos, Gauss, vamos a repetir el sorteo… ¿Dónde está Gauss?
–Creo que se quedó frito escuchando la explicación…
















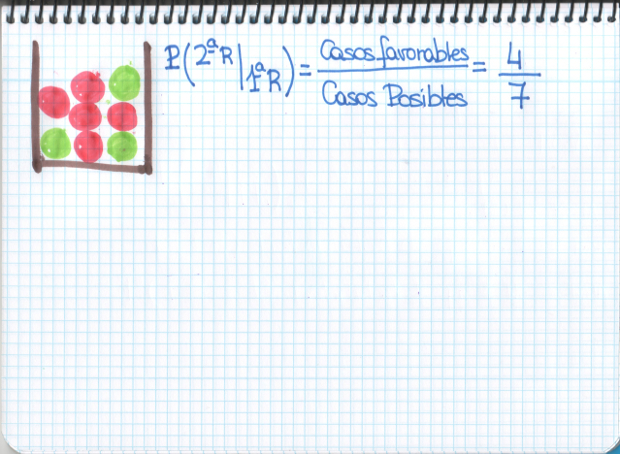




Me ha gustado tu explicación. Es interesante y sencilla de entender. Podías hablar en otro post de la estadística y la distribución. De hecho, hay un dato incorrecto en tu apunte. Los Pelayos triunfaron precisamente haciendo cálculos de distribución, no de probabilidad, que a priori, en un ruleta perfecta (o una moneda perfecta) debería estar uniformemente distribuída. La cuestión es precisamente es que existen pequeñas imperfecciones que hacen que una moneda caiga más de un lado que del otro, por ejemplo, o que una ruleta siempre pare más en un número determinado. Eso es estadística. Y de eso se valieron para ver cuál era el nº con mayor frecuencia y apostar.
Un saludo,
don Pimplón
13 junio 2012 | 11:30
En la primitva las quinielas y todo eso, tales calculos no valen pues hay millones de posibilidades Solo la suerte es la que manda. Y la suerte es una señora loca, como casi todo en esta vida.
Clica sobre mi nombre
13 junio 2012 | 11:31
Muy interesante la explicación, muy guapa, pero hagamos que nazca otra variable, ni cara, ni cruz, sino que quede de canto.
Viendo a Rihanna últimamente, su moda, ¿qué probabilidad existe de que en un país que se dice libre se acepte la verdad natural humana? ¿Existe alguna probabilidad de que el ser humano, el bípedo que ha evolucionado tan a tropezones y malamente, que se llama ahora ecologista y natural, pierda miedo a sus cadenas prohibitivas y censoras contra sí mismo y deje de tachar de indigno, de sucio, algo tan verdad, tan bello, como la natura humana? Creo que existe mayor probabilidad de que una parábola se convierta en triángulo que el ser humano renazca nuevamente, pero pacífica e inteligentemente.
¿Cara, cruz a que esta moda avanza? POnemos la variable del tiempo en el canto, como siempre pasa
http://egotastic.com/photos/rihanna-takes-a-stroll-in-a-see-through-top-in-nyc/rihanna-in-a-see-through-top-in-nyc-05/
13 junio 2012 | 11:48