Hoy vamos a hablar del metro, pero no de tarifazos ni de noticias que nos ponen mal cuerpo, vamos a intentar abstraernos durante unos minutos de la realidad.
Hoy vamos a hablar del metro, pero no de tarifazos ni de noticias que nos ponen mal cuerpo, vamos a intentar abstraernos durante unos minutos de la realidad.
Hoy, y ahora que los niños salieron a jugar, vamos a hablar de planos de metro, concretamente del plano del metro de Londres, y de cómo un desconocido ingeniero consiguió revolucionar parte de los conceptos de diseño en el siglo XX.
¿Que qué tiene que ver esto con Matemáticas?
Pues, mucho. Es el ejemplo que algunos de los que enseñamos Teoría de Grafos usamos para mostrar a nuestros estudiantes la importancia de la representación, el dibujo, de un grafo.
¿Qué es un grafo?
De forma coloquial y sencilla, un grafo es un conjunto de elementos, a los que llamaremos vértices, que se relacionan entre ellos por parejas, no necesariamente todos, definiendo lo que llamamos aristas del grafo.
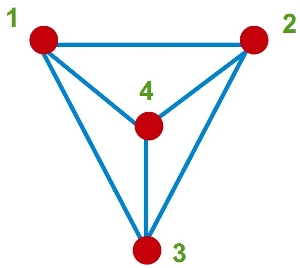
Podemos pensar, por ejemplo que queremos diseñar un circuito con 4 componentes, todas unidos con todas, por parejas. A las componentes, que harán el papel de vértices del grafo, las llamamos en una alarde de originalidad {1, 2, 3, 4}. En ese caso, las conexiones que tenemos que dibujar, que harán el papel de aristas, serán {(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}. Al grafo así definido se le conoce como K4.
Vamos a dibujar el circuito. Una posible representación sería ésta.
Está bonita, sí. Pero es que… no queremos que las conexiones se corten entre ellas. Pensamos un poco más el posible diseño del circuito y nos damos cuenta de que si lo pintamos, por ejemplo, como en la siguiente figura, no hay cruce entre las conexiones.
¡Bingo!
Bueno, este circuito ha sido muy fácil y hemos resuelto el problema del cruce de las conexiones sin despeinarnos. Vamos a poner una componente más, una ná más. Tenemos que dibujar 5 vértices, las 5 componentes, {1, 2, 3, 4, 5} y unir cada una de ellas con las otras 4.
Muy mono, sí. Pero, ¿lo podemos dibujar sin cruces?
Les dejo unos minutos para que lo intenten.
No, no se agobien, no es posible. De hecho es uno de los teoremas más famosos de la Teoría de Grafos, el Teorema de Kuratowski.
Hasta aquí espero haberles convencidos de la importancia del dibujo de un grafo como aplicación, por ejemplo, en el diseño de circuito.
¿Qué tiene todo esto que ver con el mapa del metro de Londres?
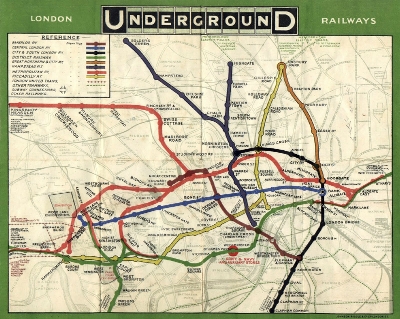
Los primeros mapas del metro de Londres eran geográficos, básicamente, consistían en dibujar sobre un plano de la ciudad los recorridos de las distintas líneas.
Fue Harry Beck, ingeniero electrónico (para que no digan que sólo hablo de matemáticos) empleado en el metro de Londres, el primero que se percató de que al usuario no le interesaba conocer el recorrido del metro bajo tierra, sino simplemente, conocer la posición relativa de las líneas y estaciones para realizar los trasbordos que necesitase.
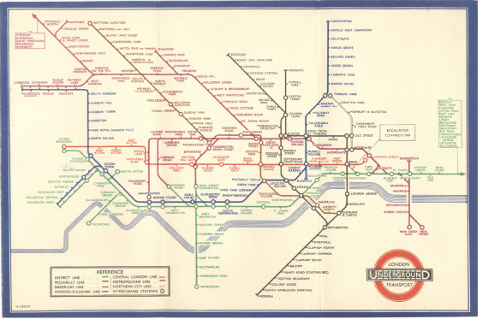
Se le ocurrió entonces, en 1931, que en realidad, más que un diseño geográfico, lo que resultaría útil sería un diseño topológico, con menos curvas y direcciones en las líneas, y, de broma, hizo su primer diseño basado en los utilizados en circuitos eléctricos. Aún un poco reticentes, lanzaron la idea de Beck entre los usuarios y fue aceptada con entusiasmo por los pasajeros del metro.
Y hasta hoy, esa idea topológica del mapa de Beck, es la más utilizada en el mundo para este tipo de planos. Esto es, sin tener en cuenta la situación geográfica de las estaciones en el mapa de la ciudad, salvo su posición respecto al Támesis, en el caso del mapa del metro de Londres. Incluso hasta en nuestro metro de Sevilla, aunque aquí, sinceramente, aún podríamos permitirnos el geográfico.
Volviendo al de Londres y a la pregunta de que qué tiene que ver el plano de un metro con las Matemáticas, en general, o con la Teoría de Grafos, en particular, pues, eso, que es otro ejemplo más, como el del diseño de circuitos sin cruces, de la importancia del dibujo de un grafo. Puesto que podemos entender las estaciones como vértices y las líneas como aristas.
De hecho, Beck, a lo largo de su trayectoria, introdujo diversos cambios a su diseño original en pos de conseguir mayor claridad en el plano.
En 1936, entre otros cambios, eliminó curvas y sólo permitió ángulos de 45º y 90º.
En 1940, le pidieron, entre otros detalles, que incorporase ángulos de 60º también, idea que se desechó posteriormente por enturbiar la claridad del plano.
 Se puede consultar aquí la evolución de los mapas de del metro de Londres y observar qué tipo de modificaciones iban apareciendo siempre para mejorar la usabilidad de los mismos, hasta llegar a la versión actual en la que, como no puede ser de otra manera, se referencia a Harry Beck como creador del diseño. Diseño que habida cuenta de la cantidad de merchandising que ha generado (camisetas, tazas, etc.) debe haber sido uno de los más rentables del siglo pasado, supongo.
Se puede consultar aquí la evolución de los mapas de del metro de Londres y observar qué tipo de modificaciones iban apareciendo siempre para mejorar la usabilidad de los mismos, hasta llegar a la versión actual en la que, como no puede ser de otra manera, se referencia a Harry Beck como creador del diseño. Diseño que habida cuenta de la cantidad de merchandising que ha generado (camisetas, tazas, etc.) debe haber sido uno de los más rentables del siglo pasado, supongo.
Pues todo esto para decidir cómo dibujar las líneas de metro y las distintas estaciones. Pero hay otro problema a la hora de diseñar mapas que es el de poner etiquetas con los nombres, por ejemplo, de las estaciones. Tienen que ser pequeños para que las dimensiones del mapa completo no sean desmesuradas pero lo suficientemente grandes para que el usuario las pueda leer. De este tipo de problemas, del de etiquetado de mapas también se ocupan investigadores matemáticos e informáticos, pero eso se escapa de este café que estamos compartiendo hablando de Beck.
De lo que no hay duda es de que la idea original de Harry Beck, aparte de su utilidad práctica, es también un hermoso ejemplo de arte.
Yo me bajo en ésta. Hasta la próxima.