 En estos días compruebo, sin alegría, que la palabra rescate ha perdido el cariz romántico. Ése que de pequeña olía a príncipe soso cabalgando sobre un caballo (no sé por qué blanco) con una capa al viento y que unos años más tarde se transformaba en un arqueólogo tocado con un sombrero Fedora y un látigo en la mano. Y sé que no soy la única, lamentablemente. Estoy segura de que cada uno de nosotros tiene en sus recuerdos de sueños infantiles o púberes rescatadores y/o rescatadoras muy diferentes… Eso sí, casi seguro que ninguno de nosotros soñó con que lo rescataba aquella chica que nacía en Hamburgo un día de julio de 1954…
En estos días compruebo, sin alegría, que la palabra rescate ha perdido el cariz romántico. Ése que de pequeña olía a príncipe soso cabalgando sobre un caballo (no sé por qué blanco) con una capa al viento y que unos años más tarde se transformaba en un arqueólogo tocado con un sombrero Fedora y un látigo en la mano. Y sé que no soy la única, lamentablemente. Estoy segura de que cada uno de nosotros tiene en sus recuerdos de sueños infantiles o púberes rescatadores y/o rescatadoras muy diferentes… Eso sí, casi seguro que ninguno de nosotros soñó con que lo rescataba aquella chica que nacía en Hamburgo un día de julio de 1954…
Pero hoy es lunes y los niños han salido a jugar, las noticias ya nos saturan de problemas que no sabemos resolver, o que, al menos no se están resolviendo, así que dejemos a los profesionales que nos informen sobre ellos y vamos a plantear un problema que nos sirva para pensar un rato y que poder compartir a la hora del café o del aperitivo con nuestros amigos, por si estamos cansados de hablar de cómo está la cosa.
El pasado viernes tuve la suerte de poder asistir a la conferencia Magia y Matemáticas que el Dr. Carlos Vinuesa impartió en la Facultad de Matemáticas de la Universidad de Sevilla. Aparte de la indiscutible capacidad de Carlos para atraer y sorprender con sus juegos de magia, los asistentes a la misma pudimos entrar entre bambalinas y descubrir qué Matemáticas se escondían detrás de aquella magia. No, no voy a contar los secretos de Vinuesa, os invito a que lo vayáis a a ver si tenéis ocasión.
Pero si os voy a contar un problema que él nos recordó en su conferencia y que es conocido como el Problema de Flavio Josefo. En su obra La guerra de los judíos, obra que algunos ponen un poco en tela de juicio en cuanto a su rigor y neutralidad, puesto que fue escrita después de que Josefo fuera capturado por los romanos y se le nota un pelín filorromana, este historiador judío cuenta como él y 40 soldados judíos quedaron atrapados en una cueva, rodeados de romanos, y que prefiririeron suicidarse antes que entregarse a los romanos. Si, hay gente pa tó. Pero como estaban así, en plan festivo, decidieron ir ejecutando a las víctimas de una forma original, no hay que perder el buen humor en ninguna situación: ¡que no se diga! Hay varias versiones sobre el método elegido para el macabro sorteo, pero la más extendida es la siguiente:
Se colocan todos los soldados en un círculo, el primero se salva, matamos al segundo, saltamos uno, matamos al cuarto, saltamos uno, matamos al siguiente, saltamos uno… y así sucesivamente hasta que queda el último que se matará sólo.
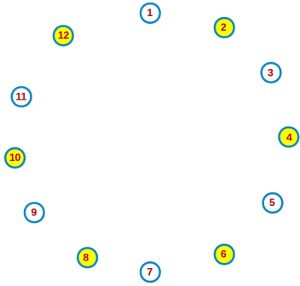
Si tenemos 12 soldados alrededor del círculo, en la primera vuelta, mataríamos a los que aparecen en amarillo en la siguiente figura
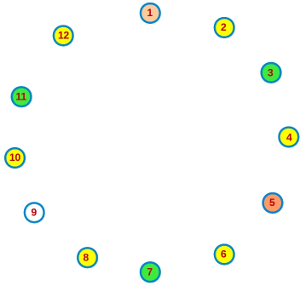
Al llegar al 12, que en paz descanse, nos saltaríamos al 1 de nuevo (ya se ha escapado 2 veces) e iríamos a por el 3. Vamos que al final de la segunda vuelta, habrían caído los que aparecen en verde en la siguiente figura
Pues bien, de nuevo tras despedirnos del 11, volvemos a saltar el 1, le damos boleto al 5, nos saltamos al 9 y nos queda…
Por lo tanto, el último que queda tras esta estrategia graciosa es el 9.
Nota mental: si somos 12 en la rueda, colocarme en la posición número 9.
Según la historia de Flavio Josefo aquel día en la cueva, al final sólo quedaron él y un amigo, que decidieron entregarse a los romanos antes que suicidarse. Dicen que él atribuyó su salvación a la Providencia. No me voy a meter en esto, pero a lo mejor es que Flavio y su colega habían hecho bien las cuentas…
¿Qué cuentas son las que hay que hacer para ser el último y decidir si suicidarte o echarte unas risas con los romanos?
Bueno, ya hemos visto que si son 12 en la rueda, la posición que más mola es la 9. Vamos a estudiar otros casos, a ver si inferimos algún método…
Si sólo somos 4 jugadores el último en morir sería el que estuviese en la posición 1…
Si hay 5 jugadores en círculo, el que se salva es el de la posición 3…
Cuando hay 6 en el círculo, se salva el 5…
La 7 es la posición buena cuando son 7…
Otra vez la posición 1, si son 8… Vamos a recoger todos estos datos en una tabla a ver si nos sugieren alguna regla…
Si nos fijamos en la tabla anterior, que para eso también lo hemos coloreado en amarillo canario, la posición 1 es la última en ser elegida en todas las ruedas cuyo número de jugadores es una potencia de 2 (1, 2, 4, 8, 16…) Luego, entre cada dos potencias de 2, lo que aparece es la sucesión de los impares, comenzando con el 3 justo después de dicha potencia de 2.
¿Se cumple siempre? Pues sí, se cumplirá siempre, otro día os contaré la demostración. Hoy nos quedamos sólo con el truco, aunque preferiría que lo usarais para otra cosa que no sea una ronda de suicidios a la salud de algún imperio. Es más gracioso, por ejemplo, para elegir quién paga una ronda en un bar, que lo pague el último en salvarse.
Para comprobar si lo he explicado con claridad, vamos a poner otro ejemplo. Supongamos que tenemos 27 países que forman una posible comunidad y que empiezan a sobrar algunos. Supongamos que aplicamos el método del problema del Josefo para ir eliminando uno a uno a estos países, ¿en qué posición hay que colocarse para ser el último en salir de esta comunidad? Vamos a hacer las cuentas. Buscamos la potencia de 2 más próxima a 27 pero inferior a él. Como 27 está entre 16 y 32, la potencia buscada es 16, 2 elevado a 4. Ahora, si queréis en una tablita, rellenáis con impares hasta llegar al 27…
Pues sí, para ser el último en salir hay que colocarse en la posición 23 en la rueda, que viene a caer un poco al sur del mar Báltico, un poco a la izquierda de Polonia y sin llegar a Francia…








Este es el cambio que necesita España:
http://reflexionesglobalesynotanto.blogspot.com.es/2012/06/mi-argumentario.html?spref=tw
04 junio 2012 | 9:33