–A, 5.

–¡Agua!

–No puede ser, Ven, ¿¿has puesto algún barco??

–¡Pues, claro! ¿Qué crees, Sal? ¿Que no sé jugar a los barquitos? –contestó el pequeño.

–Es que es imposible que no haya encontrado aún ninguno… –protestó el gafotas.

 

 

–Buenas tardes, caballeros… –Mati acababa de llegar.

–¡Hola, Mati! –saludaron los niños al unísono.

–¿Jugáis a las batalles navales? Me encanta ese juego –contestó la pelirroja.

–Y a mí. Pero Sal no consigue encontrar ninguno de mis barcos -respondió Ven con cara de pícaro. Su hermano lo miró serio por encima de sus gafitas.

–Además de que es un juego divertido es un buen método para aprender las coordenadas cartesianas –-añadió Mati.

–¿¿El qué?? –preguntaron los dos con los ojos abiertos de par en par.

–Las coordenadas cartesianas, que son, podríamos decir, como el nombre y el apellido de los puntos en un plano, para poder distinguirlos unos de otros, sin posibilidad de confundirlos.

–No entiendo nada –aceptó el pequeño Ven.

–Si Sal te dice “D,6”, Ven, ¿tienes alguna duda de dónde está apuntando?

–¡Toma, claro que no! A éste -señaló Ven con su dedo sobre el papel –Miro dónde se cruzan la fila D y la columna 6 y ya está.

–Pues así es cómo se asignan las coordenadas cartesianas a cualquier punto del plano. Os lo explico con un dibujo.

–¡Sí! -contestaron con alegría los dos hermanitos.

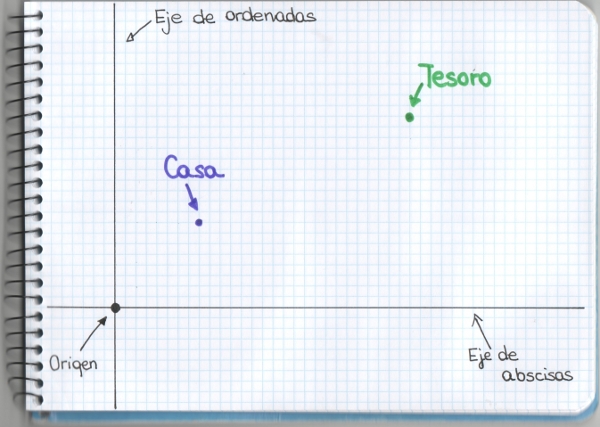
–Lo que queremos es saber identificar cualquier punto de un plano, porque, por ejemplo, vamos a esconder un tesoro y luego vamos a venir a buscarlo… Aquí está nuestra casa y aquí enterramos nuestro tesoro.

–Como piratas, ¿no?

–Sí, Ven, ¡como piratas! –prosiguió Mati – Lo primero que tenemos que hacer para poder asignar coordenadas a cada punto del plano y poder saber exactamente dónde escondimos el tesoro, es elegir un punto especial al que llamaremos origen, origen de coordenadas ¿Dónde lo ponemos?

–Aquí –Sal señaló un punto sobre el papel.

–Muy bien. Ahora dibujamos dos rectas perpendiculares que se cortan en el origen.

–¿Qué son perpendiculares, Mati?

–Que se cortan formando cuatro ángulos rectos, como los de la esquina de una portería.

 

–Como si fueran el signo + de la suma, ¿no, Mati? –preguntó el gafotas.

–Exacto, Sal, pero en grandote, uno vertical, de arriba a abajo, y otro horizontal, de izquierda a derecha. Al horizontal le llamaremos eje de abscisas y al vertical, eje de ordenadas.

–Ahora vamos a dividir estos ejes, usando como unidad de medida, por ejemplo, dos cuadraditos del papel. Hacia la derecha y hacia arriba, los numeramos con números naturales, positivos. Y a la izquierda y hacía abajo, les pondremos un signo – delante, para distinguirlos.

–Ahora, para conocer cuáles son las coordenadas de nuestra casa y de nuestro tesoro, dibujamos una línea vertical desde el punto donde está hasta encontrar al eje de abscisas, y una linea horizontal hasta encontrar al eje de ordenadas. Con estas dos líneas y los ejes, tendremos dos rectángulos, en los que nuestros puntos, la casa y el tesoro, serán una de las esquinas. Por eso, a estas coordenadas también se le llaman coordenadas rectangulares. Pues bien, las coordenadas de nuestros puntos serán: la primera, el número marcado en el eje de abscisas y la segunda el número marcado en el eje de ordenadas. Por eso, a la primera coordenada de un punto se le llama la abscisa y a la segunda, se le llama la ordenada.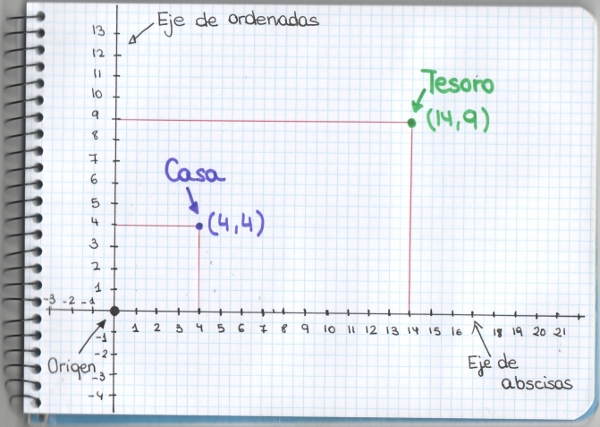

–Nuestra casa tiene la misma abscisa que ordenada, Mati –observó Sal.

–Sí, es verdad, en este caso el rectángulo es un cuadrado, tiene los lados iguales.

–Y la abscisa del tesoro es 14 y la ordenada es 9, ¿no? –siguió indagando el gafotas.

–Exacto –respondió la pelirroja.

–¡Toma, toma, toma! ¡Cómo mola, Mati! Así siempre encontraremos el tesoro –el pequeño Ven estaba alucinando.

–¿Y por qué le llamas cartesianas? ¿Porque a los mapas también se le llaman cartas? –preguntó Sal.

–No, no. El nombre de cartesianas de lo debe a René Descartes, filósofo y matemático francés, que sostenía que la visión que tenemos de las cosas depende de dónde hayamos fijado el origen de coordenadas –Mati guiñó un ojo, los niños no dijeron nada.

–¿Está muerto? –preguntó Ven con carita de pena.

–Sí, hace mucho tiempo, en 1650 –contestó la pelirroja mientras le acariciaba el pelo —Oye, ¿queréis saber también para que podemos usar las coordenadas cartesianas aparte de señalar exactamente un lugar del plano?

–¡Claro!

–Para conocer la distancia entre dos puntos del plano sin necesidad de ir a medirlo.

–¿Cómo? –quiso saber el gafotas excitado.

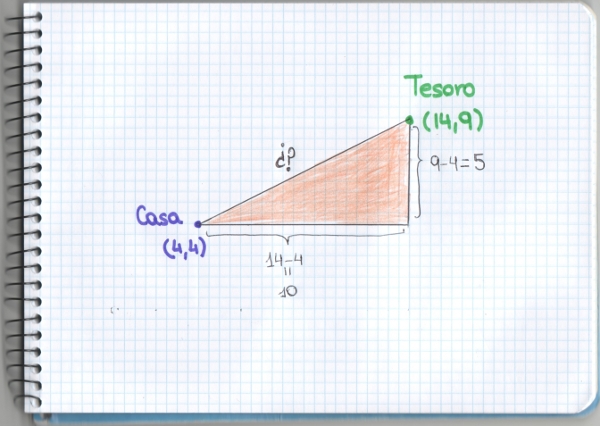
–Dibujamos un triángulo de la siguiente manera.

–Es un triángulo rectángulo, porque tiene un ángulo recto, donde se cortan el lado vertical y el horizontal. Al lado más largo de un triángulo rectángulo, se le llama hipotenusa, que en nuestro dibujo es el que queremos medir. Y a los otros dos lados del triángulo, les llamamos catetos…

–Pobres…–dijo Ven.

Mati no pudo evitar la sonrisa.

–¿Cuánto miden los catetos? Ya vereís. El lado horizontal mide la diferencia entre las dos primeras coordenadas, las abscisas; el lado vertical mide la diferencia entre las dos segundas coordenadas, las ordenadas.

–¡Claro! -Sal estaba entusiasmado.

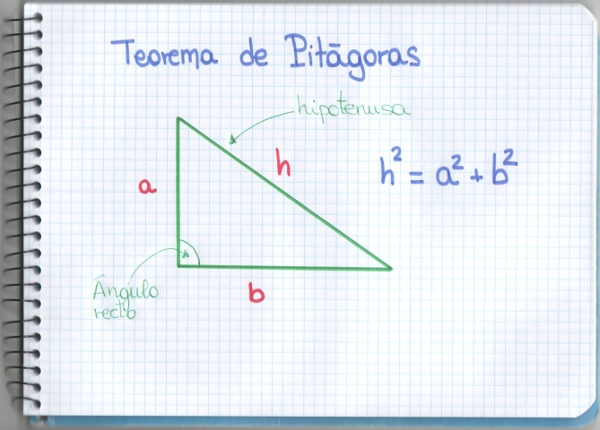
–Ahora, para saber cuánto mide la hipotenusa que es la distancia de nuestra casa al tesoro, sólo necesitamos el Teorema de Pitágoras.

–¿Cómo, Mati? –los niños estaban ansiosos esperando la respuesta final.

–Pues así

 

–¡Toma, Mati! ¡Y sin necesidad de medir! -Ven estaba entusiasmado.

–Pero ni Ven ni yo sabemos calcular raíces cuadradas, Mati –aceptó el gafotas serio.

–Por ahora, yo os ayudo. Ya lo aprenderemos.

–Entonces, ¿así lo hacen los piratas, Mati? –preguntó el pequeño.

–Bueno, los piratas tenían otra forma de asignar coordenadas… Os la explico otro día. Vamos a pasear a Gauss que está deseando buscar algún tesoro en el parque.